Q-Learning

什么是 Q-Learning ？

Q学习是强化学习中基于价值的学习算法。

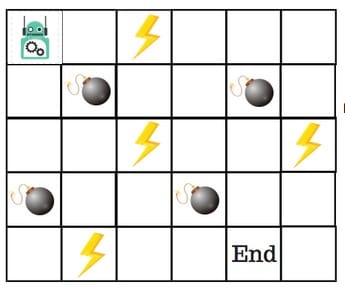
假设机器人必须越过迷宫并到达终点。有地雷，机器人一次只能移动一个地砖。如果机器人踏上矿井，机器人就死了。机器人必须在尽可能短的时间内到达终点。

得分/奖励系统如下：

1. 机器人在每一步都失去1点。这样做是为了使机器人采用最短路径并尽可能快地到达目标。
2. 如果机器人踩到地雷，则点损失为100并且游戏结束。
3. 如果机器人获得动力⚡️，它会获得1点。
4. 如果机器人达到最终目标，则机器人获得100分。

现在，显而易见的问题是：我们如何训练机器人以最短的路径到达最终目标而不踩矿井？

那么，我们该如何解决这个问题呢？

 

什么是 Q-Table ？

Q-Table只是一个简单查找表的奇特名称，我们计算每个州的最大预期未来奖励。基本上，这张表将指导我们在每个州采取最佳行动。

每个非边缘区块将有四个动作数。当机器人处于某种状态时，它可以向上或向下或向右或向左移动。

所以，让我们在Q-Table中对这个环境进行建模。

在Q表中，列是动作，行是状态。

每个Q表得分将是机器人在该状态下采取该行动时将获得的最大预期未来奖励。这是一个迭代过程，因为我们需要在每次迭代时改进Q-Table。

但问题是：

• 我们如何计算Q表的值？
• 值是可用的还是预定义的？

为了学习Q表的每个值，我们使用Q-Learning算法。

 

Q-Learning 的数学依据

Q-Fuction

所述 Q-Fuction 使用Bellman方程和采用两个输入：状态（小号）和动作（一个）。

使用上面的函数，我们得到表中单元格的Q值。

当我们开始时，Q表中的所有值都是零。

有一个更新值的迭代过程。当我们开始探索环境时，通过不断更新表中的Q值， Q函数为我们提供了更好和更好的近似。

现在，让我们了解更新是如何进行的。

 

Q-Learning 算法的过程详解

每个彩色框都是一步。让我们详细了解每个步骤。

第1步：初始化Q表

我们将首先构建一个Q表。有n列，其中n =操作数。有m行，其中m =状态数。我们将值初始化为0。

在我们的机器人示例中，我们有四个动作（a = 4）和五个状态（s = 5）。所以我们将构建一个包含四列五行的表。

步骤2和3：选择并执行操作

这些步骤的组合在不确定的时间内完成。这意味着此步骤一直运行，直到我们停止训练，或者训练循环停止，如代码中所定义。

我们将根据Q-Table选择状态中的动作（a）。但是，如前所述，当剧集最初开始时，每个Q值都为0。

因此，现在探索和开发权衡的概念发挥作用。

我们将使用一种叫做epsilon贪婪策略的东西。

一开始，ε利率会更高。机器人将探索环境并随机选择动作。这背后的逻辑是机器人对环境一无所知。

随着机器人探索环境，epsilon率降低，机器人开始利用环境。

在探索过程中，机器人逐渐变得更有信心估计Q值。

对于机器人示例，有四种操作可供选择：向上，向下，向左和向右。 我们现在开始训练 – 我们的机器人对环境一无所知。所以机器人选择随机动作，说对了。

我们现在可以使用Bellman方程更新Q值，使其处于开始和向右移动。

步骤4和5：评估

现在我们采取了行动并观察了结果和奖励。我们需要更新功能Q（s，a）。

在机器人游戏的情况下，重申得分/奖励结构是：

• 功率 = +1
• 我的 = -100
• 结束 = +100

我们将一次又一次地重复这一过程，直到学习停止。通过这种方式，Q表将会更新。

本文翻译自《An introduction to Q-Learning: reinforcement learning》

 

维基百科版本