超大型語言模型如何能夠完成您的想法?通過可視化的方式來看看OpenAI 的 GPT-2 是如何生成文章的。讓我們看看可視化是否可以幫助我們更好地理解這個模型。
Author Archive
「免費」吳恩達新課程《TensorFlow:從入門到精通》
《TensorFlow:從入門到精通》是 Deeplearning.ai 的一系列實踐課程,由吳恩達老師參與開發並執教,除了吳恩達老師,該課程的另一重量級教師為 Laurence Moroney 博士。
Adaboost 演算法

首先,了解一下集成學習及 Boosting 演算法
集成學習歸屬於機器學習,他是一種「訓練思路」,並不是某種具體的方法或者演算法。
現實生活中,大家都知道「人多力量大」,「3 個臭皮匠頂個諸葛亮」。而集成學習的核心思路就是「人多力量大」,它並沒有創造出新的演算法,而是把已有的演算法進行結合,從而得到更好的效果。
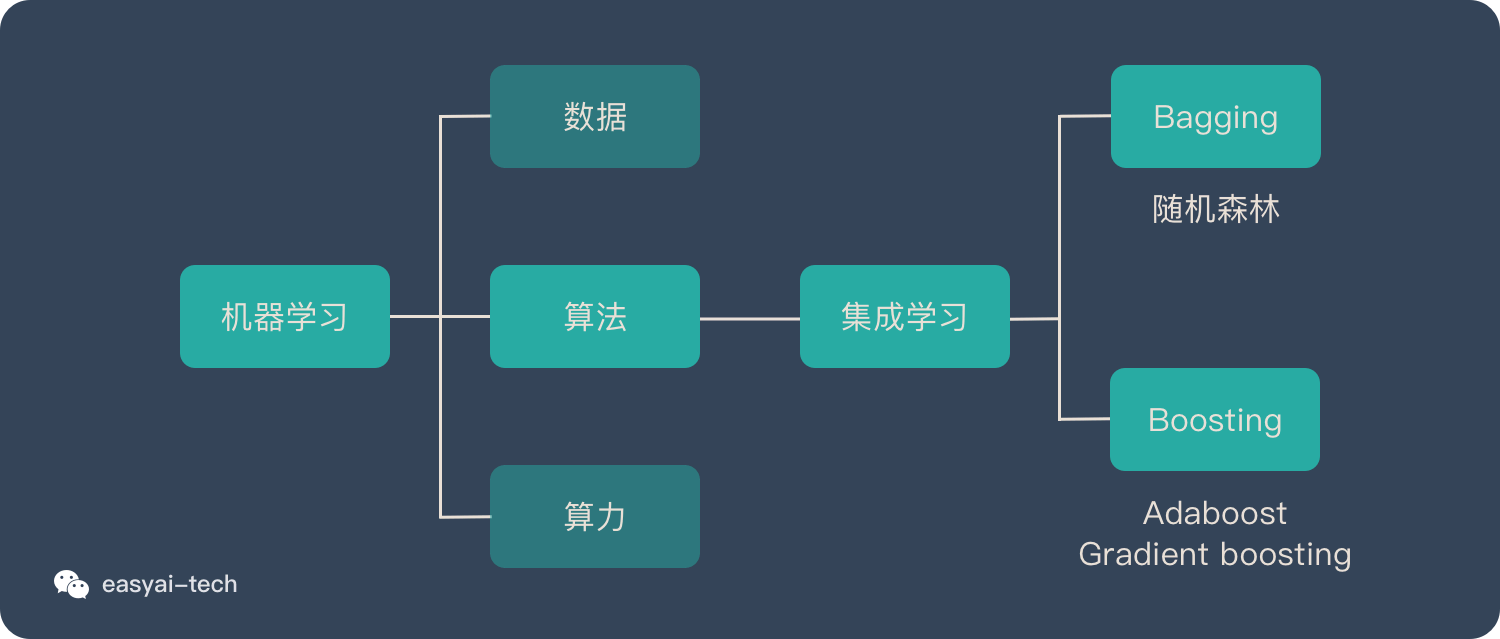
集成學習會挑選一些簡單的基礎模型進行組裝,組裝這些基礎模型的思路主要有 2 種方法:
- bagging(bootstrap aggregating的縮寫,也稱作「套袋法」)
- boosting
今天所說的 Adaboost 演算法就是 Boosting演算法的其中一種。
下面再說一下Boosting演算法:

Boosting 的核心思路是——挑選精英。
Boosting 和 bagging 最本質的差別在於他對基礎模型不是一致對待的,而是經過不停的考驗和篩選來挑選出「精英」,然後給精英更多的投票權,表現不好的基礎模型則給較少的投票權,然後綜合所有人的投票得到最終結果。
大部分情況下,經過 boosting 得到的結果偏差(bias)更小。
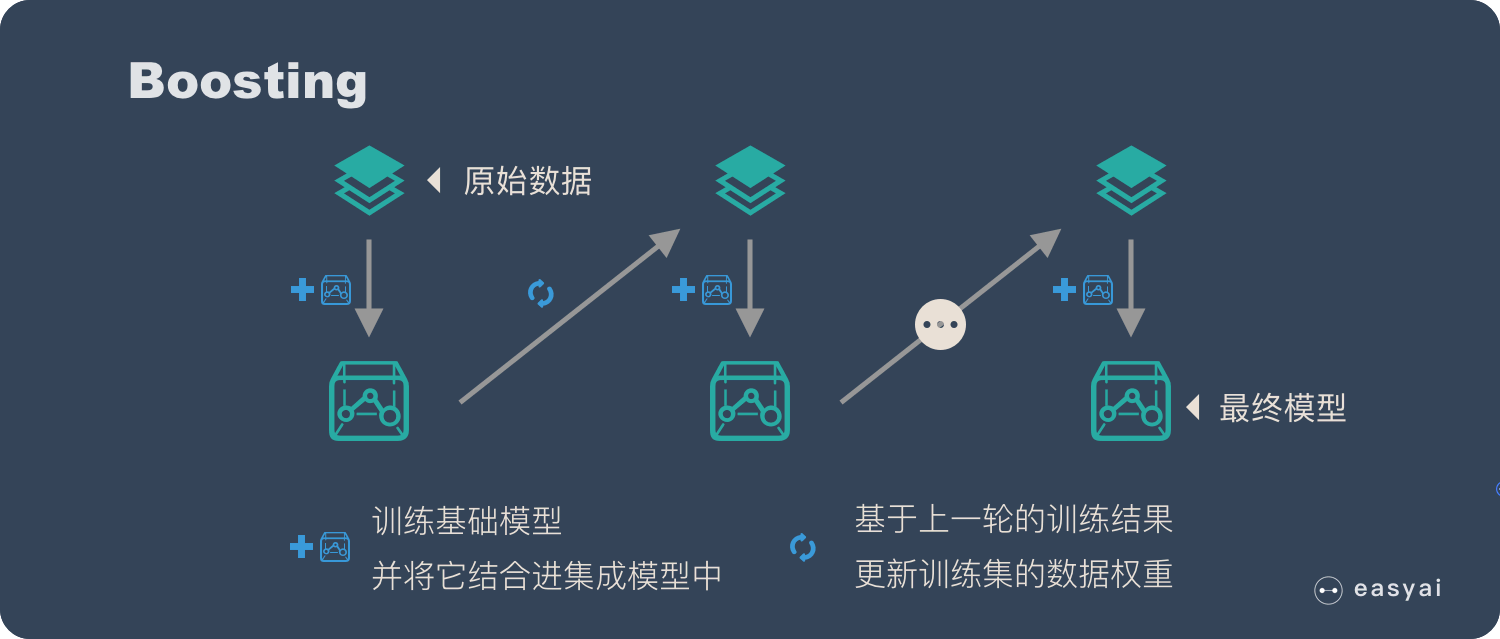
具體過程:
- 通過加法模型將基礎模型進行線性的組合。
- 每一輪訓練都提升那些錯誤率小的基礎模型權重,同時減小錯誤率高的模型權重。
- 在每一輪改變訓練數據的權值或概率分布,通過提高那些在前一輪被弱分類器分錯樣例的權值,減小前一輪分對樣例的權值,來使得分類器對誤分的數據有較好的效果。
想要詳細了解集成演算法或bagging演算法,可以看看這篇文章《一文看懂集成學習(詳解 bagging、boosting 以及他們的 4 點區別)》
什麼是 AdaBoost 演算法?
Boosting是一種集合技術,試圖從許多弱分類器中創建一個強分類器。這是通過從訓練數據構建模型,然後創建第二個模型來嘗試從第一個模型中糾正錯誤來完成的。添加模型直到完美預測訓練集或添加最大數量的模型。
AdaBoost是第一個為二進位分類開發的真正成功的增強演算法。這是理解助力的最佳起點。現代助推方法建立在AdaBoost上,最著名的是隨機梯度增強機。
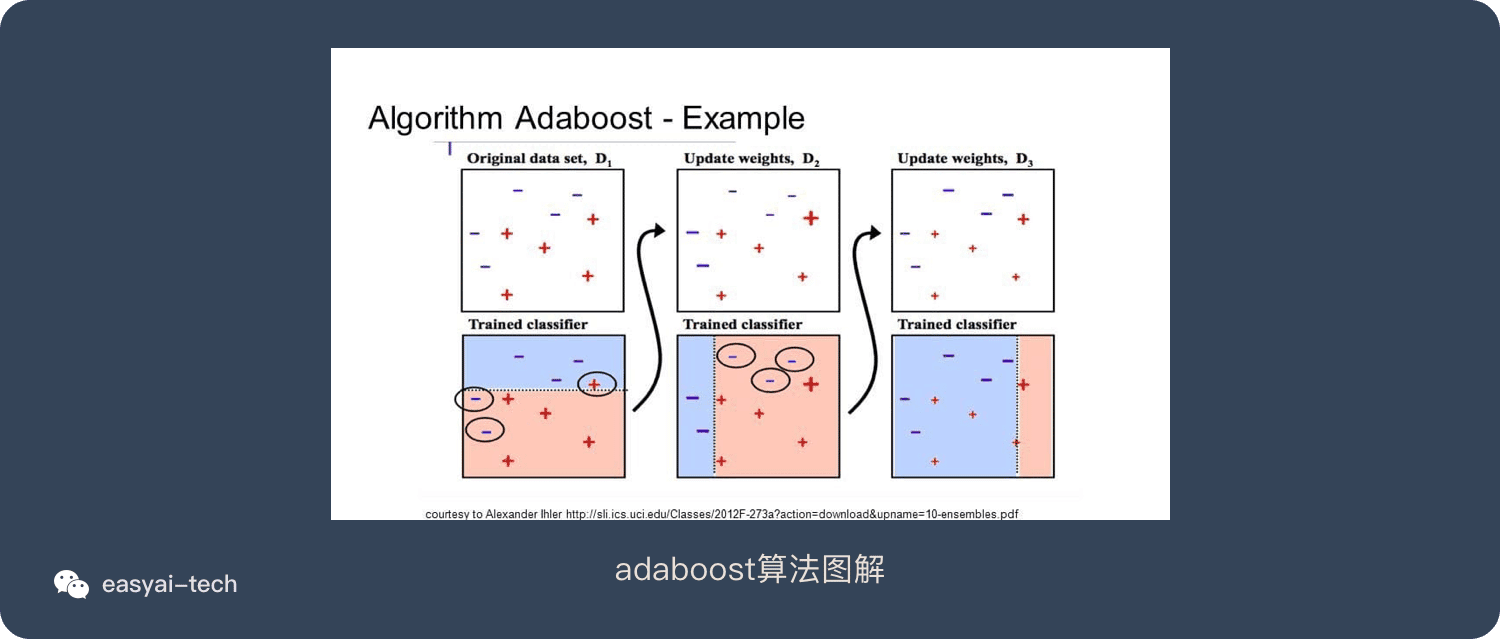
AdaBoost用於短決策樹。在創建第一個樹之後,每個訓練實例上的樹的性能用於加權創建的下一個樹應該關注每個訓練實例的注意力。難以預測的訓練數據被賦予更多權重,而易於預測的實例被賦予更少的權重。模型一個接一個地順序創建,每個模型更新訓練實例上的權重,這些權重影響序列中下一個樹所執行的學習。構建完所有樹之後,將對新數據進行預測,並根據訓練數據的準確性對每棵樹的性能進行加權。
因為通過演算法如此關注糾正錯誤,所以必須刪除帶有異常值的乾淨數據。
Adaboost 的 7 個優缺點

AdaBoost演算法優點:
- 很好的利用了弱分類器進行級聯;
- 可以將不同的分類演算法作為弱分類器;
- AdaBoost具有很高的精度;
- 相對於bagging演算法和Random Forest演算法,AdaBoost充分考慮的每個分類器的權重;
Adaboost演算法缺點:
- AdaBoost迭代次數也就是弱分類器數目不太好設定,可以使用交叉驗證來進行確定;
- 數據不平衡導致分類精度下降;
- 訓練比較耗時,每次重新選擇當前分類器最好切分點;
百度百科和維基百科
Adaboost是一種迭代演算法,其核心思想是針對同一個訓練集訓練不同的分類器(弱分類器),然後把這些弱分類器集合起來,構成一個更強的最終分類器(強分類器)。
AdaBoost是Adaptive Boosting的縮寫,是由Yoav Freund和Robert Schapire製作的機器學習 元演算法,他們因其工作而獲得2003年哥德爾獎。它可以與許多其他類型的學習演算法結合使用,以提高性能。其他學習演算法(「弱學習者」)的輸出被組合成加權和,該加權和表示提升分類器的最終輸出。
AdaBoost在某種意義上是適應性的,即隨後的弱學習者被調整為支持那些被先前分類器錯誤分類的實例。AdaBoost對雜訊數據和異常值敏感。在某些問題中,它可能比其他學習演算法更不容易受到過度擬合問題的影響。個體學習者可能很弱,但只要每個學習者的表現略好於隨機猜測,最終的模型就可以證明可以融合到強大的學習者身上。
隨機森林 – Random forest

隨機森林是一種由決策樹構成的集成演算法,他在很多情況下都能有不錯的表現。
本文將介紹隨機森林的基本概念、4 個構造步驟、4 種方式的對比評測、10 個優缺點和 4 個應用方向。
什麼是隨機森林?
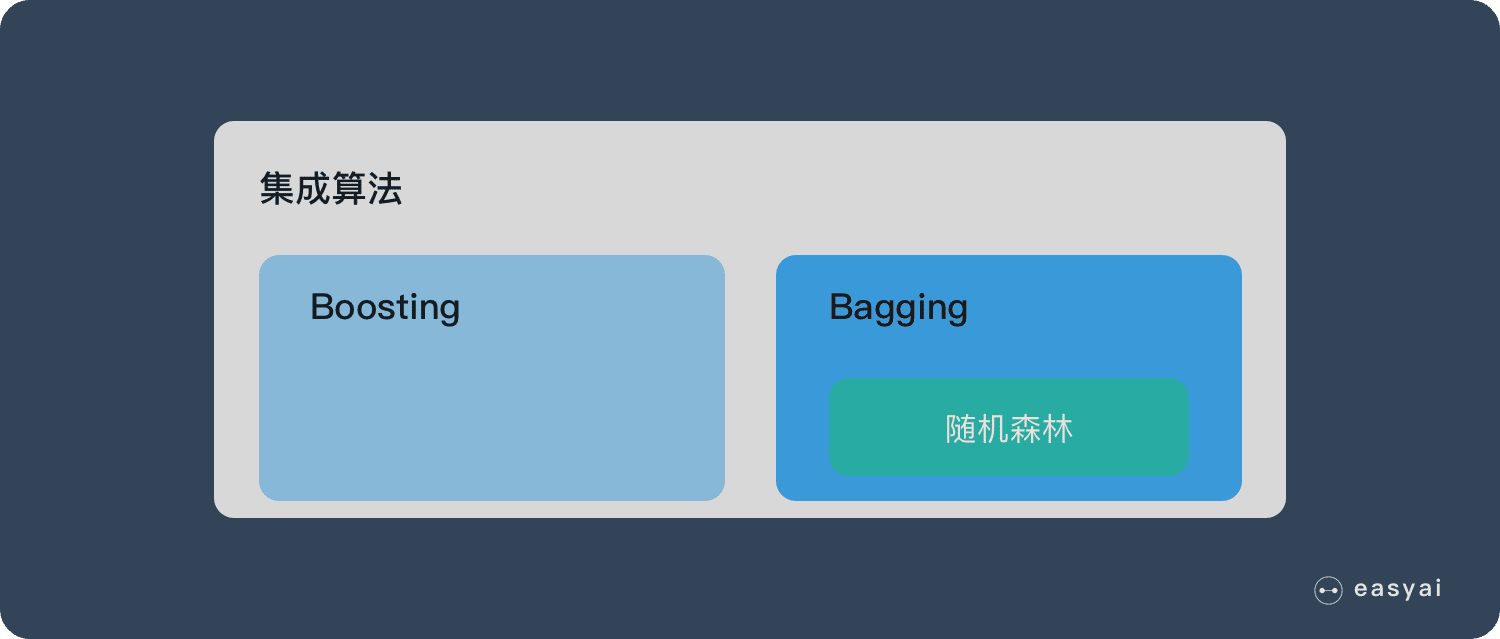
隨機森林屬於 集成學習 中的 Bagging(Bootstrap AGgregation 的簡稱) 方法。如果用圖來表示他們之間的關係如下:
決策樹 – Decision Tree
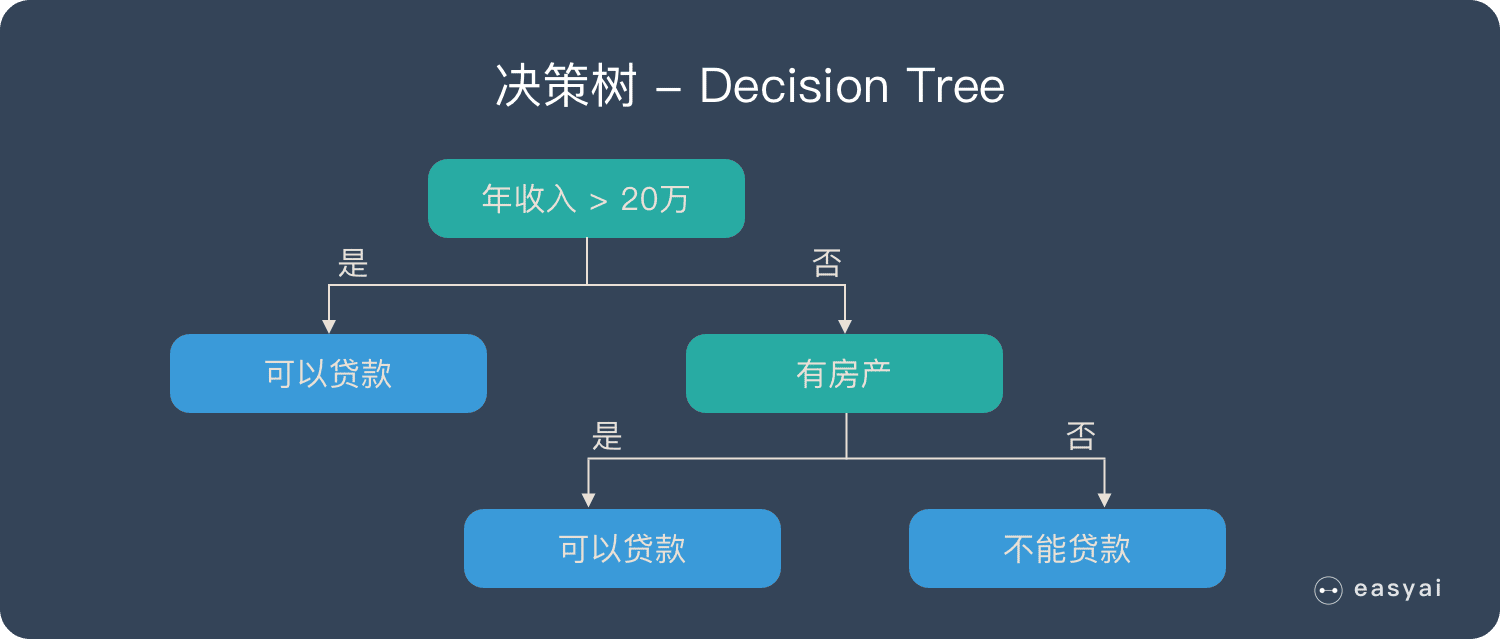
在解釋隨機森林前,需要先提一下決策樹。決策樹是一種很簡單的演算法,他的解釋性強,也符合人類的直觀思維。這是一種基於if-then-else規則的有監督學習演算法,上面的圖片可以直觀的表達決策樹的邏輯。
了解詳情:《一文看懂決策樹 – Decision tree(3個步驟+3種典型演算法+10個優缺點)》
隨機森林 – Random Forest | RF
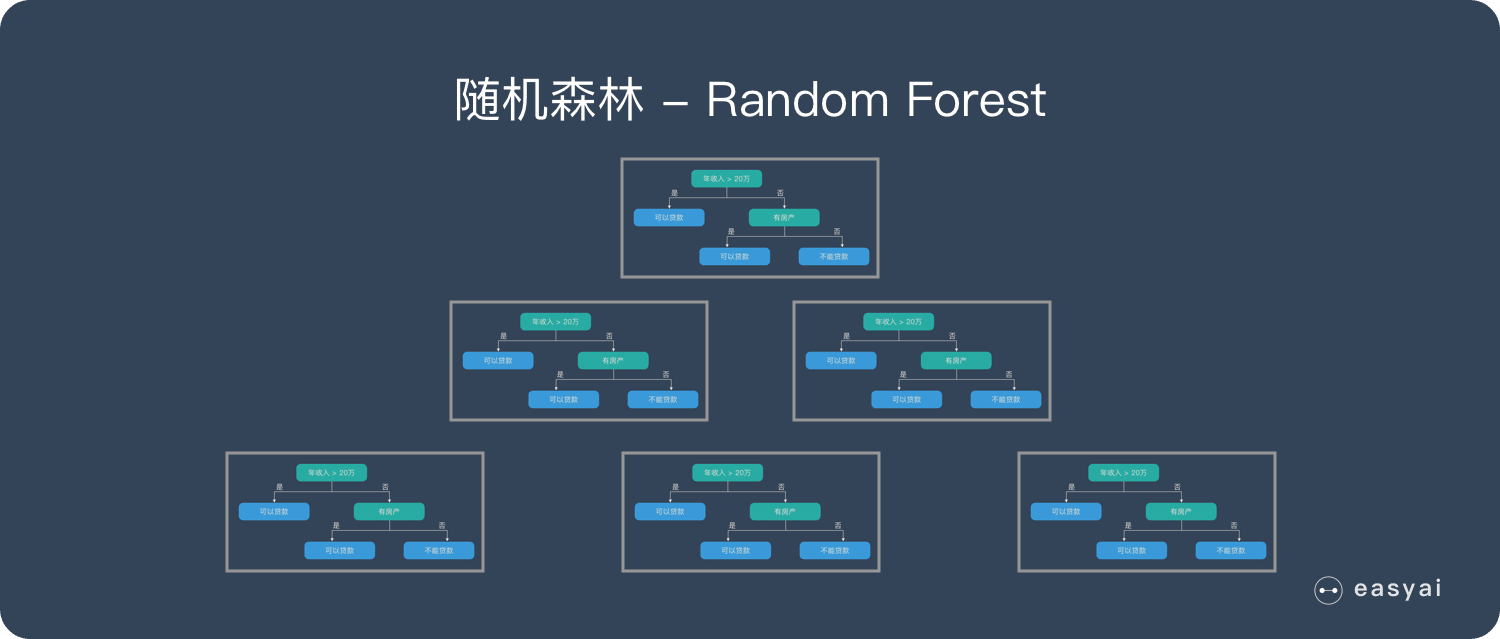
隨機森林是由很多決策樹構成的,不同決策樹之間沒有關聯。
當我們進行分類任務時,新的輸入樣本進入,就讓森林中的每一棵決策樹分別進行判斷和分類,每個決策樹會得到一個自己的分類結果,決策樹的分類結果中哪一個分類最多,那麼隨機森林就會把這個結果當做最終的結果。
構造隨機森林的 4 個步驟

- 一個樣本容量為N的樣本,有放回的抽取N次,每次抽取1個,最終形成了N個樣本。這選擇好了的N個樣本用來訓練一個決策樹,作為決策樹根節點處的樣本。
- 當每個樣本有M個屬性時,在決策樹的每個節點需要分裂時,隨機從這M個屬性中選取出m個屬性,滿足條件m << M。然後從這m個屬性中採用某種策略(比如說信息增益)來選擇1個屬性作為該節點的分裂屬性。
- 決策樹形成過程中每個節點都要按照步驟2來分裂(很容易理解,如果下一次該節點選出來的那一個屬性是剛剛其父節點分裂時用過的屬性,則該節點已經達到了葉子節點,無須繼續分裂了)。一直到不能夠再分裂為止。注意整個決策樹形成過程中沒有進行剪枝。
- 按照步驟1~3建立大量的決策樹,這樣就構成了隨機森林了。
隨機森林的優缺點
優點
- 它可以出來很高維度(特徵很多)的數據,並且不用降維,無需做特徵選擇
- 它可以判斷特徵的重要程度
- 可以判斷出不同特徵之間的相互影響
- 不容易過擬合
- 訓練速度比較快,容易做成並行方法
- 實現起來比較簡單
- 對於不平衡的數據集來說,它可以平衡誤差。
- 如果有很大一部分的特徵遺失,仍可以維持準確度。
缺點
- 隨機森林已經被證明在某些噪音較大的分類或回歸問題上會過擬合。
- 對於有不同取值的屬性的數據,取值劃分較多的屬性會對隨機森林產生更大的影響,所以隨機森林在這種數據上產出的屬性權值是不可信的
隨機森林 4 種實現方法對比測試
隨機森林是常用的機器學習演算法,既可以用於分類問題,也可用於回歸問題。本文對 scikit-learn、Spark MLlib、DolphinDB、XGBoost 四個平台的隨機森林演算法實現進行對比測試。評價指標包括內存佔用、運行速度和分類準確性。
測試結果如下:
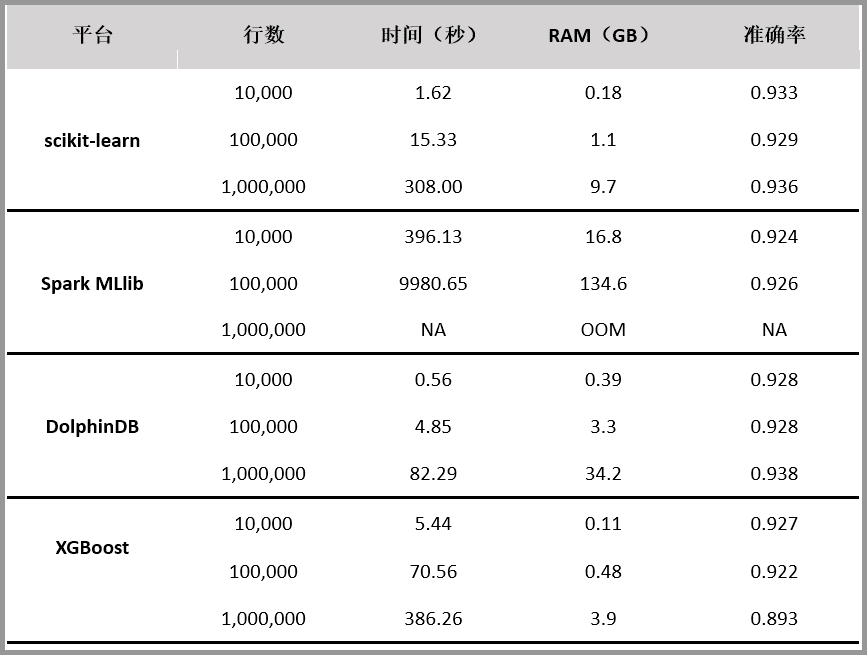
測試過程及說明忽略,感興趣的可以查看原文《隨機森林演算法 4 種實現方法對比測試:DolphinDB 速度最快,XGBoost 表現最差》
隨機森林的 4 個應用方向

隨機森林可以在很多地方使用:
- 對離散值的分類
- 對連續值的回歸
- 無監督學習聚類
- 異常點檢測
百度百科+維基百科
在機器學習中,隨機森林是一個包含多個決策樹的分類器, 並且其輸出的類別是由個別樹輸出的類別的眾數而定。 Leo Breiman和Adele Cutler發展出推論出隨機森林的演算法。
隨機森林或隨機決策森林是用於分類,回歸和其他任務的集成學習方法,其通過在訓練時構建多個決策樹並輸出作為類的模式(分類)或平均預測(回歸)的類來操作。個別樹木。隨機決策森林糾正決策樹過度擬合其訓練集的習慣。
擴展閱讀
學習向量量化 – Learning vector quantization | LVQ
什麼是學習向量量化?
K鄰近演算法的缺點是你需要堅持整個訓練數據集。學習向量量化演算法(或簡稱LVQ)是一種人工神經網路演算法,允許您選擇要掛起的訓練實例數量,並準確了解這些實例應該是什麼樣子。
LVQ的表示是碼本向量的集合。這些是在開始時隨機選擇的,並且適於在學習演算法的多次迭代中最佳地總結訓練數據集。在學習之後,可以使用碼本向量來進行與K-Nearest Neighbors類似的預測。通過計算每個碼本矢量和新數據實例之間的距離來找到最相似的鄰居(最佳匹配碼本矢量)。然後返回最佳匹配單元的類值或(回歸情況下的實際值)作為預測。如果將數據重新縮放到相同範圍(例如0到1之間),則可獲得最佳結果。
如果您發現KNN在您的數據集上提供了良好的結果,請嘗試使用LVQ來降低存儲整個訓練數據集的內存要求。
百度百科版本
學習向量量化(Learning Vector Quantization,簡稱LVQ)屬於原型聚類,即試圖找到一組原型向量來聚類,每個原型向量代表一個簇,將空間劃分為若干個簇,從而對於任意的樣本,可以將它劃入到它距離最近的簇中,不同的是LVQ假設數據樣本帶有類別標記,因此可以利用這些類別標記來輔助聚類。
維基百科版本
LVQ可以被理解為人工神經網路的一個特例,更確切地說,它應用了一種贏家通吃的 Hebbian學習方法。它是自組織圖(SOM)的前體,與神經氣體有關,也與k-最近鄰演算法(k-NN)有關。LVQ由Teuvo Kohonen發明。
K鄰近 – k-nearest neighbors | KNN
什麼是 K鄰近演算法?
KNN演算法非常簡單且非常有效。KNN的模型表示是整個訓練數據集。簡單吧?
通過搜索K個最相似的實例(鄰居)的整個訓練集並總結那些K個實例的輸出變數,對新數據點進行預測。對於回歸問題,這可能是平均輸出變數,對於分類問題,這可能是模式(或最常見)類值。
訣竅在於如何確定數據實例之間的相似性。如果您的屬性具有相同的比例(例如,以英寸為單位),則最簡單的技術是使用歐幾里德距離,您可以根據每個輸入變數之間的差異直接計算該數字。

KNN可能需要大量內存或空間來存儲所有數據,但僅在需要預測時才進行計算(或學習),及時。您還可以隨著時間的推移更新和策劃您的訓練實例,以保持預測準確。
距離或接近度的概念可以在非常高的維度(許多輸入變數)中分解,這會對演算法在您的問題上的性能產生負面影響。這被稱為維度的詛咒。它建議您僅使用與預測輸出變數最相關的輸入變數。
K鄰近演算法的優缺點
優點
- 理論成熟,思想簡單,既可以用來做分類也可以用來做回歸;
- 可用於非線性分類;
- 訓練時間複雜度為O(n);
- 對數據沒有假設,準確度高,對outlier不敏感;
- KNN是一種在線技術,新數據可以直接加入數據集而不必進行重新訓練;
- KNN理論簡單,容易實現;
缺點
- 樣本不平衡問題(即有些類別的樣本數量很多,而其它樣本的數量很少)效果差;
- 需要大量內存;
- 對於樣本容量大的數據集計算量比較大(體現在距離計算上);
- 樣本不平衡時,預測偏差比較大。如:某一類的樣本比較少,而其它類樣本比較多;
- KNN每一次分類都會重新進行一次全局運算;
- k值大小的選擇沒有理論選擇最優,往往是結合K-折交叉驗證得到最優k值選擇;
百度百科版本
鄰近演算法,或者說K最近鄰(kNN,k-NearestNeighbor)分類演算法是數據挖掘分類技術中最簡單的方法之一。所謂K最近鄰,就是k個最近的鄰居的意思,說的是每個樣本都可以用它最接近的k個鄰居來代表。
kNN演算法的核心思想是如果一個樣本在特徵空間中的k個最相鄰的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別,並具有這個類別上樣本的特性。該方法在確定分類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。 kNN方法在類別決策時,只與極少量的相鄰樣本有關。由於kNN方法主要靠周圍有限的鄰近的樣本,而不是靠判別類域的方法來確定所屬類別的,因此對於類域的交叉或重疊較多的待分樣本集來說,kNN方法較其他方法更為適合。
維基百科版本
在模式識別中,k-最近鄰演算法(k -NN)是用於分類和回歸的非參數方法。在這兩種情況下,輸入都包含特徵空間中最近的k個訓練樣例。輸出取決於k -NN是用於分類還是回歸:
- 在k-NN分類中,輸出是類成員資格。對象通過其鄰居的多個投票進行分類,其中對象被分配給其k個最近鄰居中最常見的類(k是正整數,通常是小整數)。如果k = 1,則簡單地將對象分配給該單個最近鄰居的類。
- 在k-NN回歸中,輸出是對象的屬性值。該值是其k個最近鄰居的值的平均值。
k -NN是一種基於實例的學習或懶惰學習,其中函數僅在本地近似,並且所有計算都推遲到分類。該ķ -NN演算法是最簡單的所有中機器學習演算法。
線性判別分析 – Linear Discriminant Analysis | LDA
什麼是線性判別分析?
邏輯回歸是一種傳統上僅限於兩類分類問題的分類演算法。如果您有兩個以上的類,則線性判別分析演算法是首選的線性分類技術。
LDA的代表非常簡單。它包含數據的統計屬性,為每個類計算。對於單個輸入變數,這包括:
- 每個分類的平均值。
- 在所有類別中計算的方差。

通過計算每個類的判別值並對具有最大值的類進行預測來進行預測。該技術假設數據具有高斯分布(鐘形曲線),因此最好事先從數據中刪除異常值。它是分類預測建模問題的一種簡單而強大的方法。
百度百科版本
線性判別分析(linear discriminant analysis,LDA)是對費舍爾的線性鑒別方法的歸納,這種方法使用統計學,模式識別和機器學習方法,試圖找到兩類物體或事件的特徵的一個線性組合,以能夠特徵化或區分它們。所得的組合可用來作為一個線性分類器,或者,更常見的是,為後續的分類做降維處理。
維基百科版本
線性判別分析(LDA),正態判別分析(NDA)或判別函數分析是Fisher線性判別式的推廣,這是一種用於統計,模式識別和機器學習的方法,用於找出表徵或分離兩個或兩個特徵的線性特徵組合。更多類的對象或事件。得到的組合可以用作線性分類器,或者更常見地,用於在稍後分類之前降低維數。
人工智慧和數據科學的十大角色
應用數據科學是一項高度跨學科的團隊運動。透視的多樣性很重要!事實上,觀點和態度至少與教育和經驗一樣重要。如果您希望通過決策智能工程方法使數據變得有用,那麼這就是我對團隊發展的順序的看法。
關於 TensorFlow,你應該知道的 9 個重點
TensorFlow 是一個強大的機器學習框架,本文介紹關於 TensorFlow 的9個特點,主要針對想要了解 TensorFlow 的技術人員和非技術人員。同時本文還包含了大量有用的資源,可以幫助大家更全面的了解和學習。
TF-IDF
什麼是 TF-IDF 演算法?
簡單來說,向量空間模型就是希望把查詢關鍵字和文檔都表達成向量,然後利用向量之間的運算來進一步表達向量間的關係。比如,一個比較常用的運算就是計算查詢關鍵字所對應的向量和文檔所對應的向量之間的 「相關度」。
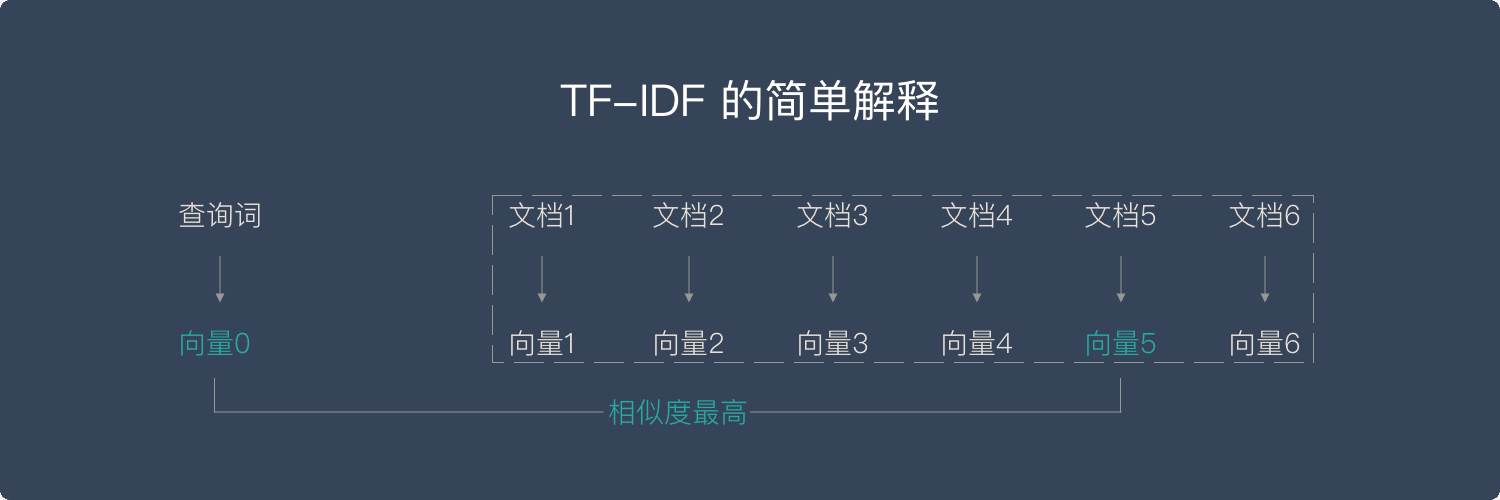
TF (Term Frequency)—— 「單詞頻率」
意思就是說,我們計算一個查詢關鍵字中某一個單詞在目標文檔中出現的次數。舉例說來,如果我們要查詢 「Car Insurance」,那麼對於每一個文檔,我們都計算「Car」 這個單詞在其中出現了多少次,「Insurance」這個單詞在其中出現了多少次。這個就是 TF 的計算方法。
TF 背後的隱含的假設是,查詢關鍵字中的單詞應該相對於其他單詞更加重要,而文檔的重要程度,也就是相關度,與單詞在文檔中出現的次數成正比。比如,「Car」 這個單詞在文檔 A 里出現了 5 次,而在文檔 B 里出現了 20 次,那麼 TF 計算就認為文檔 B 可能更相關。
然而,信息檢索工作者很快就發現,僅有 TF 不能比較完整地描述文檔的相關度。因為語言的因素,有一些單詞可能會比較自然地在很多文檔中反覆出現,比如英語中的 「The」、「An」、「But」 等等。這些詞大多起到了鏈接語句的作用,是保持語言連貫不可或缺的部分。然而,如果我們要搜索 「How to Build A Car」 這個關鍵詞,其中的 「How」、「To」 以及 「A」 都極可能在絕大多數的文檔中出現,這個時候 TF 就無法幫助我們區分文檔的相關度了。
IDF(Inverse Document Frequency)—— 「逆文檔頻率」
就在這樣的情況下應運而生。這裡面的思路其實很簡單,那就是我們需要去 「懲罰」(Penalize)那些出現在太多文檔中的單詞。
也就是說,真正攜帶 「相關」 信息的單詞僅僅出現在相對比較少,有時候可能是極少數的文檔里。這個信息,很容易用 「文檔頻率」 來計算,也就是,有多少文檔涵蓋了這個單詞。很明顯,如果有太多文檔都涵蓋了某個單詞,這個單詞也就越不重要,或者說是這個單詞就越沒有信息量。因此,我們需要對 TF 的值進行修正,而 IDF 的想法是用 DF 的倒數來進行修正。倒數的應用正好表達了這樣的思想,DF 值越大越不重要。
TF-IDF 演算法主要適用於英文,中文首先要分詞,分詞後要解決多詞一義,以及一詞多義問題,這兩個問題通過簡單的tf-idf方法不能很好的解決。於是就有了後來的詞嵌入方法,用向量來表徵一個詞。
TF-IDF 的4個變種

變種1:通過對數函數避免 TF 線性增長
很多人注意到 TF 的值在原始的定義中沒有任何上限。雖然我們一般認為一個文檔包含查詢關鍵詞多次相對來說表達了某種相關度,但這樣的關係很難說是線性的。拿我們剛才舉過的關於 「Car Insurance」 的例子來說,文檔 A 可能包含 「Car」 這個詞 100 次,而文檔 B 可能包含 200 次,是不是說文檔 B 的相關度就是文檔 A 的 2 倍呢?其實,很多人意識到,超過了某個閾值之後,這個 TF 也就沒那麼有區分度了。
用 Log,也就是對數函數,對 TF 進行變換,就是一個不讓 TF 線性增長的技巧。具體來說,人們常常用 1+Log(TF) 這個值來代替原來的 TF 取值。在這樣新的計算下,假設 「Car」 出現一次,新的值是 1,出現 100 次,新的值是 5.6,而出現 200 次,新的值是 6.3。很明顯,這樣的計算保持了一個平衡,既有區分度,但也不至於完全線性增長。
變種2:標準化解決長文檔、短文檔問題
經典的計算並沒有考慮 「長文檔」 和「短文檔」的區別。一個文檔 A 有 3,000 個單詞,一個文檔 B 有 250 個單詞,很明顯,即便 「Car」 在這兩個文檔中都同樣出現過 20 次,也不能說這兩個文檔都同等相關。對 TF 進行 「標準化」(Normalization),特別是根據文檔的最大 TF 值進行的標準化,成了另外一個比較常用的技巧。
變種3:對數函數處理 IDF
第三個常用的技巧,也是利用了對數函數進行變換的,是對 IDF 進行處理。相對於直接使用 IDF 來作為 「懲罰因素」,我們可以使用 N+1 然後除以 DF 作為一個新的 DF 的倒數,並且再在這個基礎上通過一個對數變化。這裡的 N 是所有文檔的總數。這樣做的好處就是,第一,使用了文檔總數來做標準化,很類似上面提到的標準化的思路;第二,利用對數來達到非線性增長的目的。
變種4:查詢詞及文檔向量標準化
還有一個重要的 TF-IDF 變種,則是對查詢關鍵字向量,以及文檔向量進行標準化,使得這些向量能夠不受向量里有效元素多少的影響,也就是不同的文檔可能有不同的長度。在線性代數里,可以把向量都標準化為一個單位向量的長度。這個時候再進行點積運算,就相當於在原來的向量上進行餘弦相似度的運算。所以,另外一個角度利用這個規則就是直接在多數時候進行餘弦相似度運算,以代替點積運算。
TF-IDF 的歷史
把查詢關鍵字(Query)和文檔(Document)都轉換成 「向量」,並且嘗試用線性代數等數學工具來解決信息檢索問題,這樣的努力至少可以追溯到 20 世紀 70 年代。
1971 年,美國康奈爾大學教授傑拉德 · 索爾頓(Gerard Salton)發表了《SMART 檢索系統:自動文檔處理實驗》(The SMART Retrieval System—Experiments in Automatic Document Processing)一文,文中首次提到了把查詢關鍵字和文檔都轉換成 「向量」,並且給這些向量中的元素賦予不同的值。這篇論文中描述的 SMART 檢索系統,特別是其中對 TF-IDF 及其變種的描述成了後續很多工業級系統的重要參考。
1972 年,英國的計算機科學家卡倫 · 瓊斯(Karen Spärck Jones)在《從統計的觀點看詞的特殊性及其在文檔檢索中的應用》(A Statistical Interpretation of Term Specificity and Its Application in Retrieval) 一文中第一次詳細地闡述了 IDF 的應用。其後卡倫又在《檢索目錄中的詞賦值權重》(Index Term Weighting)一文中對 TF 和 IDF 的結合進行了論述。可以說,卡倫是第一位從理論上對 TF-IDF 進行完整論證的計算機科學家,因此後世也有很多人把 TF-IDF 的發明歸結於卡倫。
傑拉德本人被認為是 「信息檢索之父」。他 1927 年出生於德國的紐倫堡,並與 1950 年和 1952 年先後從紐約的布魯克林學院獲得數學學士和碩士學位,1958 年從哈佛大學獲得應用數學博士學位,之後來到康奈爾大學參與組建計算機系。為了致敬傑拉德本人對現代信息檢索技術的卓越貢獻,現在,美國計算機協會 ACM(Association of Computing Machinery)每三年頒發一次「傑拉德 · 索爾頓獎」(Gerard Salton Award),用於表彰對信息檢索技術有突出貢獻的研究人員。卡倫 · 瓊斯在 1988 年獲得了第二屆「傑拉德 · 索爾頓獎」 的殊榮。
備註:上面大部分內容摘抄自付費課程——《AI 技術內參》
百度百科+維基百科
TF-IDF是一種統計方法,用以評估一字詞對於一個文件集或一個語料庫中的其中一份文件的重要程度。字詞的重要性隨著它在文件中出現的次數成正比增加,但同時會隨著它在語料庫中出現的頻率成反比下降。TF-IDF加權的各種形式常被搜索引擎應用,作為文件與用戶查詢之間相關程度的度量或評級。
除了TF-IDF以外,網際網路上的搜索引擎還會使用基於鏈接分析的評級方法,以確定文件在搜尋結果中出現的順序。
在信息檢索中,tf-idf或TFIDF(術語頻率 – 逆文檔頻率的縮寫)是一種數字統計,旨在反映單詞對集合或語料庫中的文檔的重要程度。它經常被用作搜索信息檢索,文本挖掘和用戶建模的加權因子。tf-idf值按比例增加一個單詞出現在文檔中的次數,並被包含該單詞的語料庫中的文檔數量所抵消,這有助於調整某些單詞在一般情況下更頻繁出現的事實。Tf-idf是當今最受歡迎的術語加權方案之一; 數字圖書館中83%的基於文本的推薦系統使用tf-idf。
搜索引擎經常使用tf-idf加權方案的變體作為在給定用戶查詢的情況下對文檔的相關性進行評分和排序的中心工具。tf-idf可以成功地用於各種主題領域的停用詞過濾,包括文本摘要和分類。
