
什么是向量?
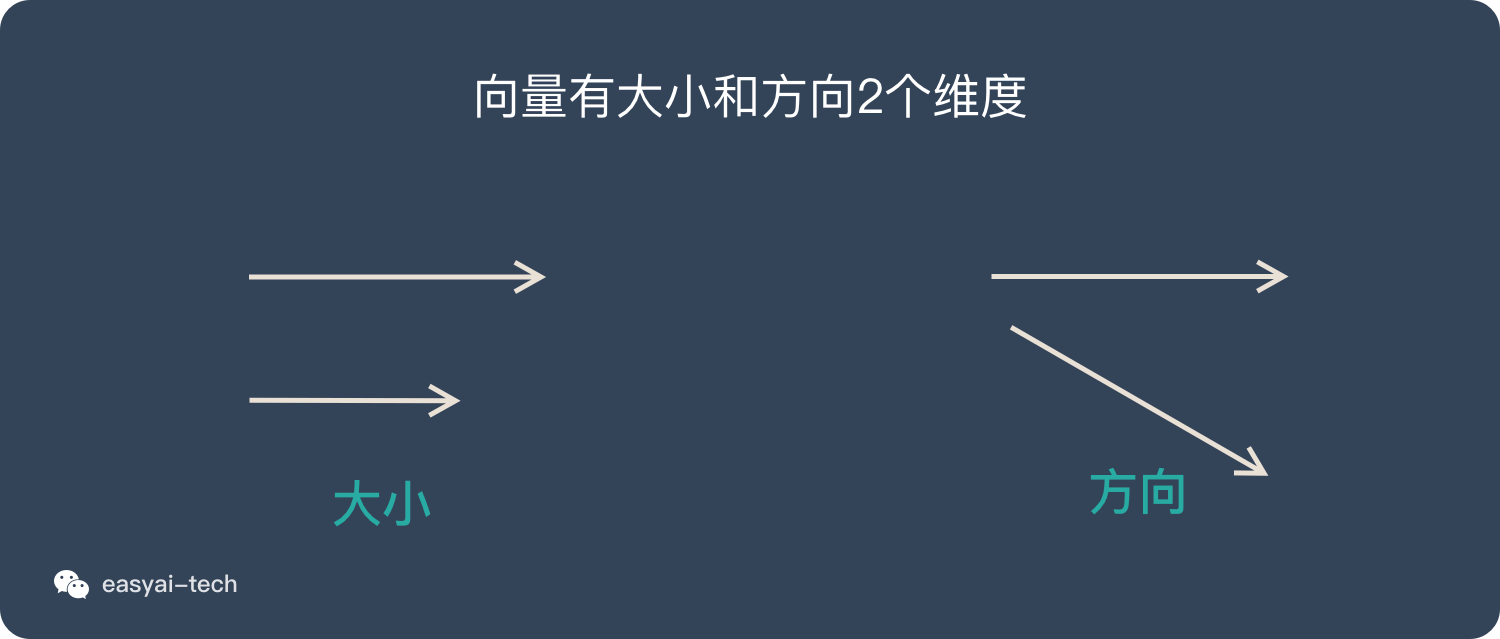
向量主要有2个维度:大小、方向。
大小:箭头的长度表示大小
方向:箭头所指的方向表示方向
向量的3种表达方式
代数表示
一般印刷用黑体的小写英文字母(a、b、c等)来表示,手写用在a、b、c等字母上加一箭头(→)表示,如
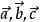
几何表示
向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。

坐标表示
在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i,j作为一组基底。a为平面直角坐标系内的任意向量,以坐标原点O为起点P为终点作向量a。由平面向量基本定理可知,有且只有一对实数(x,y),使得a=xi+yj,因此把实数对(x,y)叫做向量a的坐标,记作a=(x,y)。这就是向量a的坐标表示。其中(x,y)就是点 P 的坐标。向量a称为点P的位置向量。
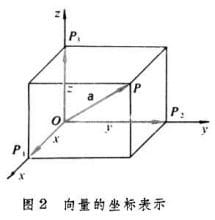
在空间直角坐标系中,分别取与x轴、y轴,z轴方向相同的3个单位向量i,j,k作为一组基底。若为该坐标系内的任意向量,以坐标原点O为起点作向量a。由空间基本定理知,有且只有一组实数(x,y,z),使得a=ix+jy+kz,因此把实数对(x,y,z)叫做向量a的坐标,记作a=(x,y,z)。这就是向量a的坐标表示。其中(x,y,z),就是点P的坐标。向量a称为点P的位置向量。
当然,对于多维的空间向量,可以通过类推得到。
向量的矩阵表示
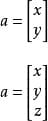
标量、向量、矩阵、张量的关系
这4个概念是维度不断上升的,我们用点线面体的概念来比喻解释会更加容易理解:

感兴趣的可以通过下面的内容了解详情:
《一文看懂标量》
《一文看懂向量》
《一文看懂矩阵》
《一文看懂张量》

百度百科和维基百科
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
向量的记法:印刷体记作黑体(粗体)的字母(如a、b、u、v),书写时在字母顶上加一小箭头“→”。 如果给定向量的起点(A)和终点(B),可将向量记作AB(并于顶上加→)。在空间直角坐标系中,也能把向量以数对形式表示,例如xOy平面中(2,3)是一向量。
向量空间(也称为线性空间)是称为对象的集合的载体,其可被添加在一起,并乘以由数字(“缩放”),所谓的标量。标量通常被认为是实数,但是也存在标量乘以复数,有理数或通常任何字段的向量空间。向量加法和标量乘法的运算必须满足下面列出的某些要求,称为公理。
欧几里德向量是向量空间的一个例子。它们代表物理量,诸如力:任何两个力(同一类型的)可被添加,以产生第三和的相乘力矢量由一实数乘法器是另一个力矢量。同样,但在更几何意义上,表示平面或三维空间中的位移的矢量也形成矢量空间。向量空间中的向量不一定必须是箭头状对象,因为它们出现在上述示例中:向量被视为具有特定属性的抽象数学对象,在某些情况下可以将其视为箭头。
向量空间是线性代数的主题,并且通过它们的维度很好地表征,粗略地说,它指定了空间中独立方向的数量。无限维向量空间在数学分析中自然出现,作为函数空间,其向量是函数。这些向量空间通常具有附加结构,其可以是拓扑结构,允许考虑接近度和连续性问题。在这些拓扑中,由规范或内积定义的拓扑更常用,因为它具有距离概念两个向量之间。特别是Banach空间和Hilbert空间的情况,这是数学分析的基础。

Comments