TF-IDF

什么是 TF-IDF 算法？

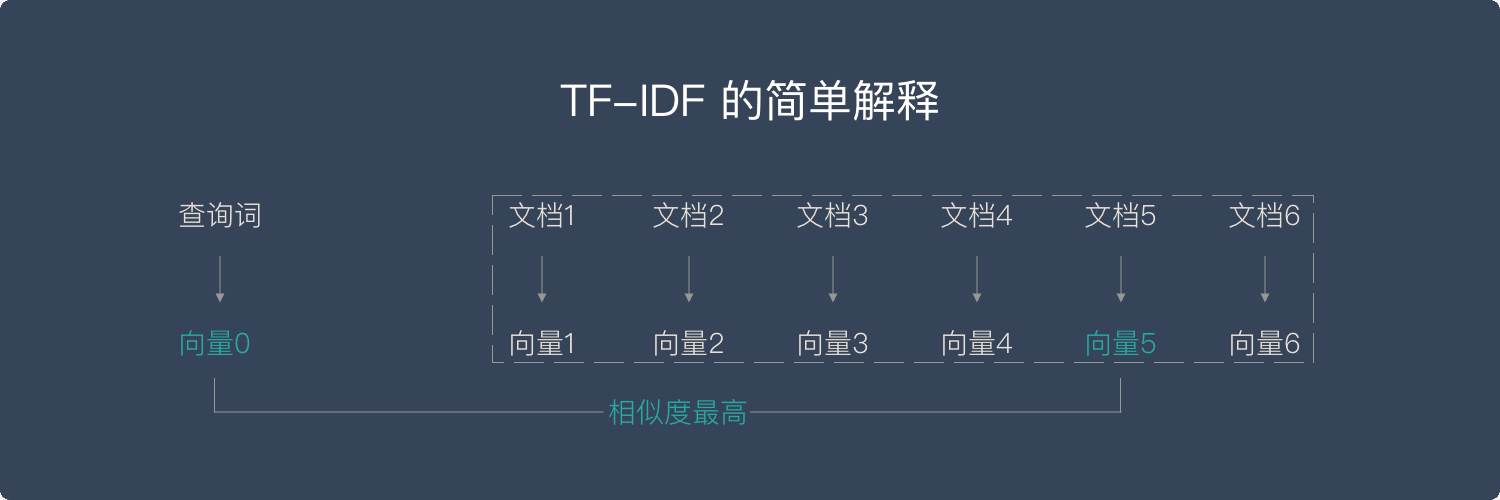
简单来说，向量空间模型就是希望把查询关键字和文档都表达成向量，然后利用向量之间的运算来进一步表达向量间的关系。比如，一个比较常用的运算就是计算查询关键字所对应的向量和文档所对应的向量之间的 “相关度”。

TF （Term Frequency）—— “单词频率”

意思就是说，我们计算一个查询关键字中某一个单词在目标文档中出现的次数。举例说来，如果我们要查询 “Car Insurance”，那么对于每一个文档，我们都计算“Car” 这个单词在其中出现了多少次，“Insurance”这个单词在其中出现了多少次。这个就是 TF 的计算方法。

TF 背后的隐含的假设是，查询关键字中的单词应该相对于其他单词更加重要，而文档的重要程度，也就是相关度，与单词在文档中出现的次数成正比。比如，“Car” 这个单词在文档 A 里出现了 5 次，而在文档 B 里出现了 20 次，那么 TF 计算就认为文档 B 可能更相关。

然而，信息检索工作者很快就发现，仅有 TF 不能比较完整地描述文档的相关度。因为语言的因素，有一些单词可能会比较自然地在很多文档中反复出现，比如英语中的 “The”、“An”、“But” 等等。这些词大多起到了链接语句的作用，是保持语言连贯不可或缺的部分。然而，如果我们要搜索 “How to Build A Car” 这个关键词，其中的 “How”、“To” 以及 “A” 都极可能在绝大多数的文档中出现，这个时候 TF 就无法帮助我们区分文档的相关度了。

IDF（Inverse Document Frequency）—— “逆文档频率”

就在这样的情况下应运而生。这里面的思路其实很简单，那就是我们需要去 “惩罚”（Penalize）那些出现在太多文档中的单词。

也就是说，真正携带 “相关” 信息的单词仅仅出现在相对比较少，有时候可能是极少数的文档里。这个信息，很容易用 “文档频率” 来计算，也就是，有多少文档涵盖了这个单词。很明显，如果有太多文档都涵盖了某个单词，这个单词也就越不重要，或者说是这个单词就越没有信息量。因此，我们需要对 TF 的值进行修正，而 IDF 的想法是用 DF 的倒数来进行修正。倒数的应用正好表达了这样的思想，DF 值越大越不重要。

TF-IDF 算法主要适用于英文，中文首先要分词，分词后要解决多词一义，以及一词多义问题，这两个问题通过简单的tf-idf方法不能很好的解决。于是就有了后来的词嵌入方法，用向量来表征一个词。

 

TF-IDF 的4个变种

变种1：通过对数函数避免 TF 线性增长

很多人注意到 TF 的值在原始的定义中没有任何上限。虽然我们一般认为一个文档包含查询关键词多次相对来说表达了某种相关度，但这样的关系很难说是线性的。拿我们刚才举过的关于 “Car Insurance” 的例子来说，文档 A 可能包含 “Car” 这个词 100 次，而文档 B 可能包含 200 次，是不是说文档 B 的相关度就是文档 A 的 2 倍呢？其实，很多人意识到，超过了某个阈值之后，这个 TF 也就没那么有区分度了。

用 Log，也就是对数函数，对 TF 进行变换，就是一个不让 TF 线性增长的技巧。具体来说，人们常常用 1+Log(TF) 这个值来代替原来的 TF 取值。在这样新的计算下，假设 “Car” 出现一次，新的值是 1，出现 100 次，新的值是 5.6，而出现 200 次，新的值是 6.3。很明显，这样的计算保持了一个平衡，既有区分度，但也不至于完全线性增长。

变种2：标准化解决长文档、短文档问题

经典的计算并没有考虑 “长文档” 和“短文档”的区别。一个文档 A 有 3,000 个单词，一个文档 B 有 250 个单词，很明显，即便 “Car” 在这两个文档中都同样出现过 20 次，也不能说这两个文档都同等相关。对 TF 进行 “标准化”（Normalization），特别是根据文档的最大 TF 值进行的标准化，成了另外一个比较常用的技巧。

变种3：对数函数处理 IDF

第三个常用的技巧，也是利用了对数函数进行变换的，是对 IDF 进行处理。相对于直接使用 IDF 来作为 “惩罚因素”，我们可以使用 N+1 然后除以 DF 作为一个新的 DF 的倒数，并且再在这个基础上通过一个对数变化。这里的 N 是所有文档的总数。这样做的好处就是，第一，使用了文档总数来做标准化，很类似上面提到的标准化的思路；第二，利用对数来达到非线性增长的目的。

变种4：查询词及文档向量标准化

还有一个重要的 TF-IDF 变种，则是对查询关键字向量，以及文档向量进行标准化，使得这些向量能够不受向量里有效元素多少的影响，也就是不同的文档可能有不同的长度。在线性代数里，可以把向量都标准化为一个单位向量的长度。这个时候再进行点积运算，就相当于在原来的向量上进行余弦相似度的运算。所以，另外一个角度利用这个规则就是直接在多数时候进行余弦相似度运算，以代替点积运算。

 

TF-IDF 的历史

把查询关键字（Query）和文档（Document）都转换成 “向量”，并且尝试用线性代数等数学工具来解决信息检索问题，这样的努力至少可以追溯到 20 世纪 70 年代。

1971 年，美国康奈尔大学教授杰拉德 · 索尔顿（Gerard Salton）发表了《SMART 检索系统：自动文档处理实验》（The SMART Retrieval System—Experiments in Automatic Document Processing）一文，文中首次提到了把查询关键字和文档都转换成 “向量”，并且给这些向量中的元素赋予不同的值。这篇论文中描述的 SMART 检索系统，特别是其中对 TF-IDF 及其变种的描述成了后续很多工业级系统的重要参考。

1972 年，英国的计算机科学家卡伦 · 琼斯（Karen Spärck Jones）在《从统计的观点看词的特殊性及其在文档检索中的应用》（A Statistical Interpretation of Term Specificity and Its Application in Retrieval） 一文中第一次详细地阐述了 IDF 的应用。其后卡伦又在《检索目录中的词赋值权重》（Index Term Weighting）一文中对 TF 和 IDF 的结合进行了论述。可以说，卡伦是第一位从理论上对 TF-IDF 进行完整论证的计算机科学家，因此后世也有很多人把 TF-IDF 的发明归结于卡伦。

杰拉德本人被认为是 “信息检索之父”。他 1927 年出生于德国的纽伦堡，并与 1950 年和 1952 年先后从纽约的布鲁克林学院获得数学学士和硕士学位，1958 年从哈佛大学获得应用数学博士学位，之后来到康奈尔大学参与组建计算机系。为了致敬杰拉德本人对现代信息检索技术的卓越贡献，现在，美国计算机协会 ACM（Association of Computing Machinery）每三年颁发一次“杰拉德 · 索尔顿奖”（Gerard Salton Award），用于表彰对信息检索技术有突出贡献的研究人员。卡伦 · 琼斯在 1988 年获得了第二届“杰拉德 · 索尔顿奖” 的殊荣。

备注：上面大部分内容摘抄自付费课程——《AI 技术内参》

 

百度百科+维基百科

 

扩展阅读