
决策树是一种逻辑简单的机器学习算法,它是一种树形结构,所以叫决策树。
本文将介绍决策树的基本概念、决策树学习的 3 个步骤、3 种典型的决策树算法、决策树的 10 个优缺点。
什么是决策树?
决策树是一种解决分类问题的算法,想要了解分类问题和回归问题,可以看这里《监督学习的2个任务:回归、分类》。
决策树算法采用树形结构,使用层层推理来实现最终的分类。决策树由下面几种元素构成:
- 根节点:包含样本的全集
- 内部节点:对应特征属性测试
- 叶节点:代表决策的结果
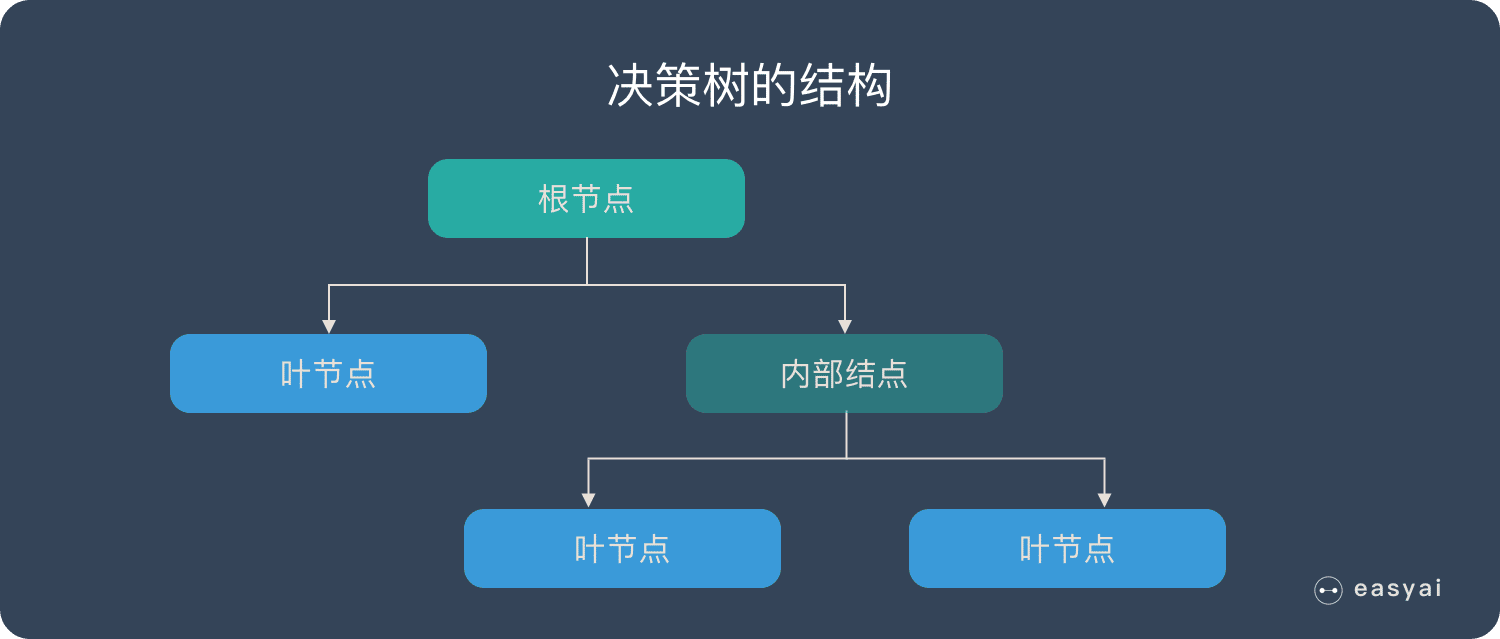
预测时,在树的内部节点处用某一属性值进行判断,根据判断结果决定进入哪个分支节点,直到到达叶节点处,得到分类结果。
这是一种基于 if-then-else 规则的有监督学习算法,决策树的这些规则通过训练得到,而不是人工制定的。
决策树是最简单的机器学习算法,它易于实现,可解释性强,完全符合人类的直观思维,有着广泛的应用。
举个栗子:
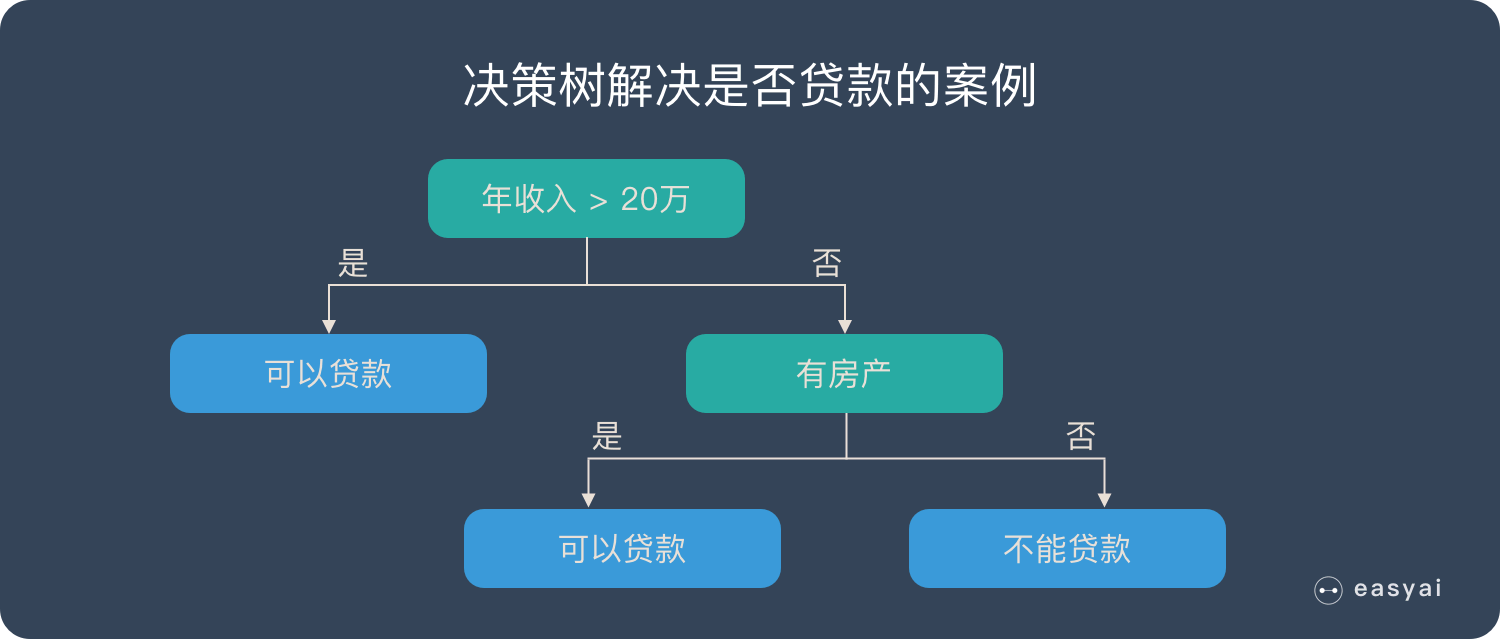
上面的说法过于抽象,下面来看一个实际的例子。银行要用机器学习算法来确定是否给客户发放贷款,为此需要考察客户的年收入,是否有房产这两个指标。领导安排你实现这个算法,你想到了最简单的线性模型,很快就完成了这个任务。
首先判断客户的年收入指标。如果大于20万,可以贷款;否则继续判断。然后判断客户是否有房产。如果有房产,可以贷款;否则不能贷款。
这个例子的决策树如下图所示:
决策树学习的 3 个步骤

特征选择
特征选择决定了使用哪些特征来做判断。在训练数据集中,每个样本的属性可能有很多个,不同属性的作用有大有小。因而特征选择的作用就是筛选出跟分类结果相关性较高的特征,也就是分类能力较强的特征。
在特征选择中通常使用的准则是:信息增益。
决策树生成
选择好特征后,就从根节点触发,对节点计算所有特征的信息增益,选择信息增益最大的特征作为节点特征,根据该特征的不同取值建立子节点;对每个子节点使用相同的方式生成新的子节点,直到信息增益很小或者没有特征可以选择为止。
决策树剪枝
剪枝的主要目的是对抗「过拟合」,通过主动去掉部分分支来降低过拟合的风险。
3 种典型的决策树算法

ID3 算法
ID3 是最早提出的决策树算法,他就是利用信息增益来选择特征的。
C4.5 算法
他是 ID3 的改进版,他不是直接使用信息增益,而是引入“信息增益比”指标作为特征的选择依据。
CART(Classification and Regression Tree)
这种算法即可以用于分类,也可以用于回归问题。CART 算法使用了基尼系数取代了信息熵模型。
决策树的优缺点
优点
- 决策树易于理解和解释,可以可视化分析,容易提取出规则;
- 可以同时处理标称型和数值型数据;
- 比较适合处理有缺失属性的样本;
- 能够处理不相关的特征;
- 测试数据集时,运行速度比较快;
- 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
缺点
- 容易发生过拟合(随机森林可以很大程度上减少过拟合);
- 容易忽略数据集中属性的相互关联;
- 对于那些各类别样本数量不一致的数据,在决策树中,进行属性划分时,不同的判定准则会带来不同的属性选择倾向;信息增益准则对可取数目较多的属性有所偏好(典型代表ID3算法),而增益率准则(CART)则对可取数目较少的属性有所偏好,但CART进行属性划分时候不再简单地直接利用增益率尽心划分,而是采用一种启发式规则)(只要是使用了信息增益,都有这个缺点,如RF)。
- ID3算法计算信息增益时结果偏向数值比较多的特征。
百度百科版本
决策树算法是一种逼近离散函数值的方法。它是一种典型的分类方法,首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。
决策树学习使用决策树(作为预测模型)从关于项目(在分支中表示)的观察到关于项目的目标值(在叶子中表示)的结论。它是统计,数据挖掘和机器学习中使用的预测建模方法之一。目标变量可以采用一组离散值的树模型称为分类树 ; 在这些树结构中,叶子代表类标签,分支代表连词导致这些类标签的功能。目标变量可以采用连续值(通常是实数)的决策树称为回归树。

Comments