超大型语言模型如何能够完成您的想法?通过可视化的方式来看看OpenAI 的 GPT-2 是如何生成文章的。让我们看看可视化是否可以帮助我们更好地理解这个模型。
Author Archive
“免费”吴恩达新课程《TensorFlow:从入门到精通》
《TensorFlow:从入门到精通》是 Deeplearning.ai 的一系列实践课程,由吴恩达老师参与开发并执教,除了吴恩达老师,该课程的另一重量级教师为 Laurence Moroney 博士。
Adaboost 算法

首先,了解一下集成学习及 Boosting 算法
集成学习归属于机器学习,他是一种“训练思路”,并不是某种具体的方法或者算法。
现实生活中,大家都知道“人多力量大”,“3 个臭皮匠顶个诸葛亮”。而集成学习的核心思路就是“人多力量大”,它并没有创造出新的算法,而是把已有的算法进行结合,从而得到更好的效果。
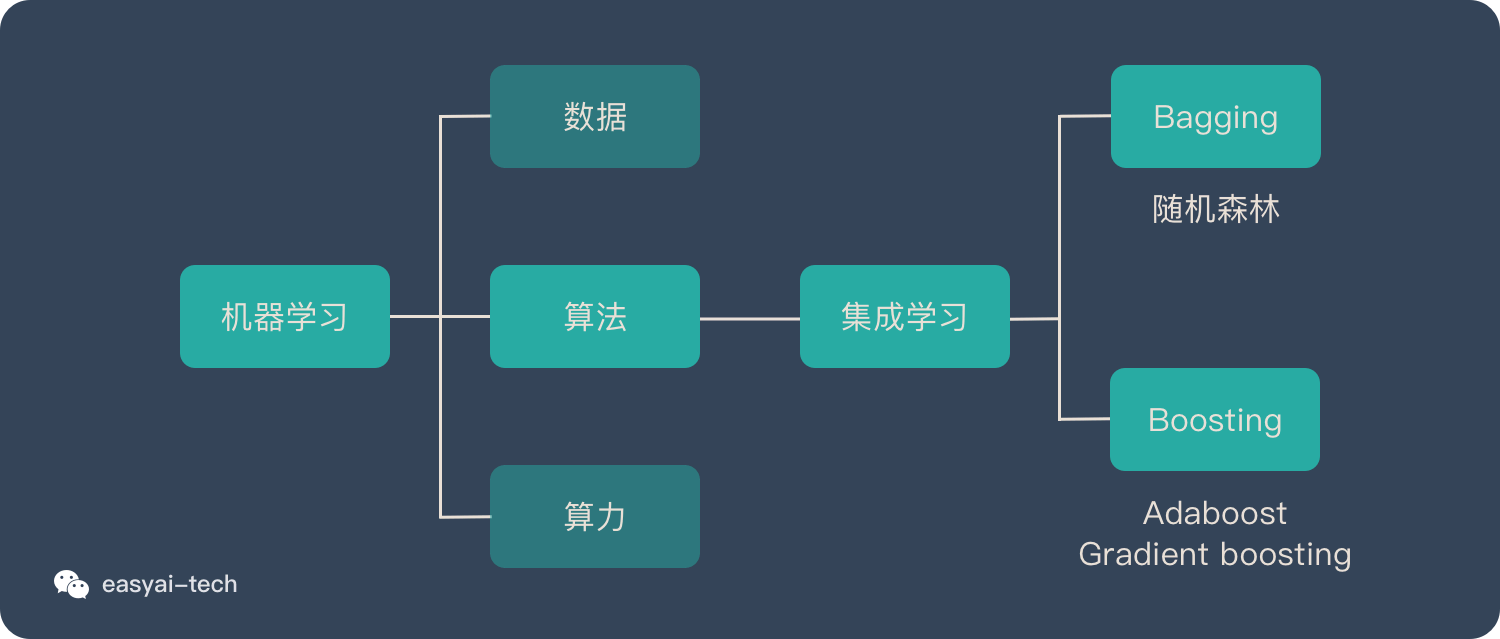
集成学习会挑选一些简单的基础模型进行组装,组装这些基础模型的思路主要有 2 种方法:
- bagging(bootstrap aggregating的缩写,也称作“套袋法”)
- boosting
今天所说的 Adaboost 算法就是 Boosting算法的其中一种。
下面再说一下Boosting算法:

Boosting 的核心思路是——挑选精英。
Boosting 和 bagging 最本质的差别在于他对基础模型不是一致对待的,而是经过不停的考验和筛选来挑选出“精英”,然后给精英更多的投票权,表现不好的基础模型则给较少的投票权,然后综合所有人的投票得到最终结果。
大部分情况下,经过 boosting 得到的结果偏差(bias)更小。
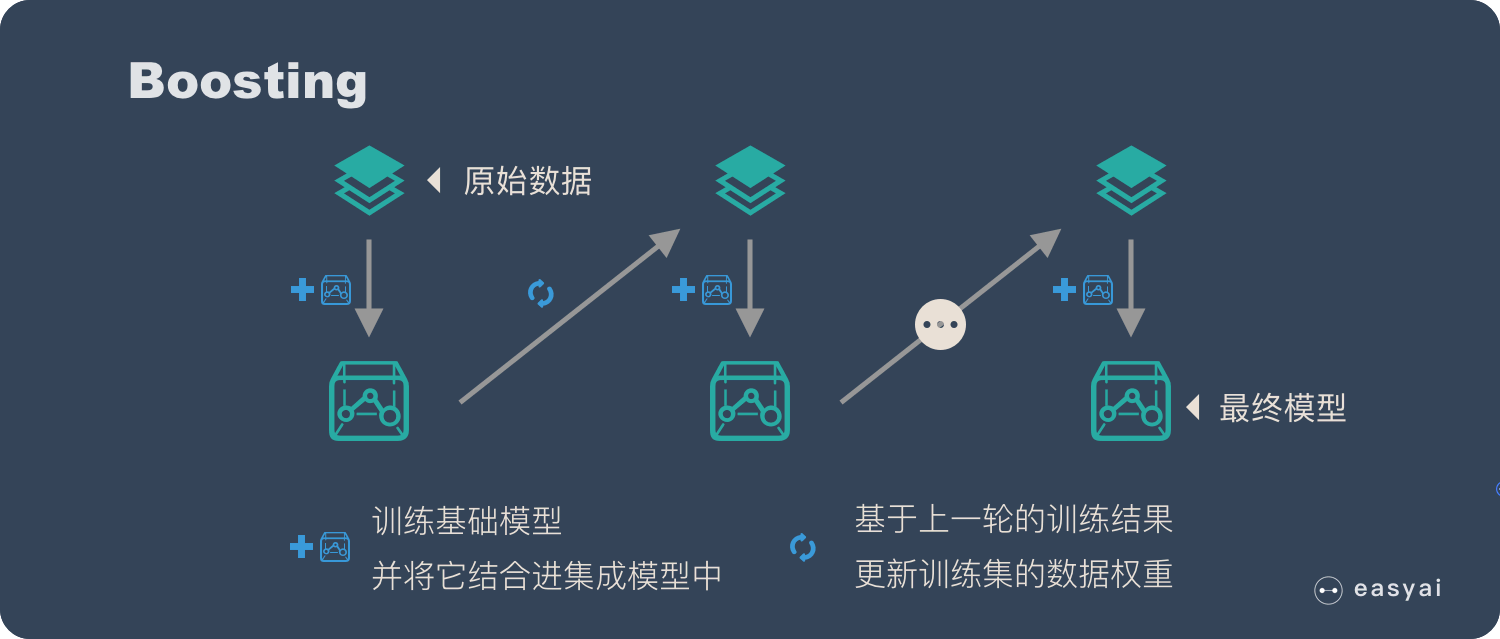
具体过程:
- 通过加法模型将基础模型进行线性的组合。
- 每一轮训练都提升那些错误率小的基础模型权重,同时减小错误率高的模型权重。
- 在每一轮改变训练数据的权值或概率分布,通过提高那些在前一轮被弱分类器分错样例的权值,减小前一轮分对样例的权值,来使得分类器对误分的数据有较好的效果。
想要详细了解集成算法或bagging算法,可以看看这篇文章《一文看懂集成学习(详解 bagging、boosting 以及他们的 4 点区别)》
什么是 AdaBoost 算法?
Boosting是一种集合技术,试图从许多弱分类器中创建一个强分类器。这是通过从训练数据构建模型,然后创建第二个模型来尝试从第一个模型中纠正错误来完成的。添加模型直到完美预测训练集或添加最大数量的模型。
AdaBoost是第一个为二进制分类开发的真正成功的增强算法。这是理解助力的最佳起点。现代助推方法建立在AdaBoost上,最着名的是随机梯度增强机。
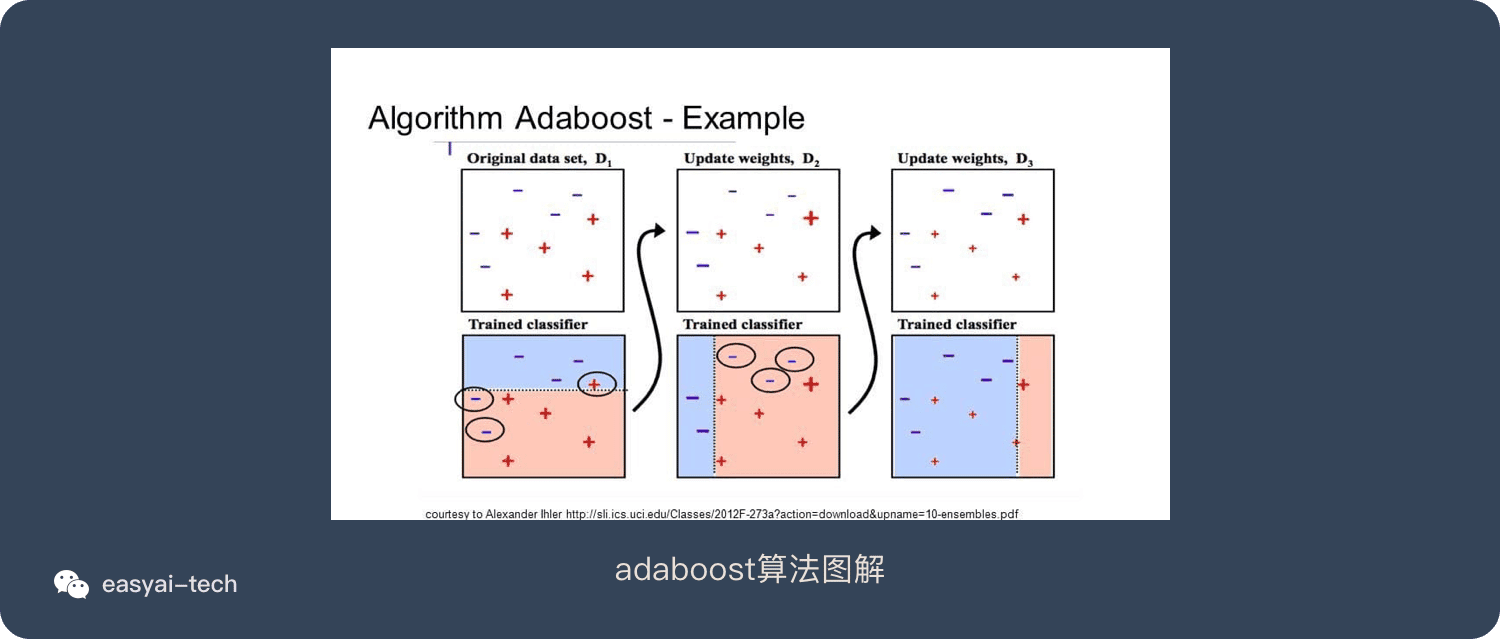
AdaBoost用于短决策树。在创建第一个树之后,每个训练实例上的树的性能用于加权创建的下一个树应该关注每个训练实例的注意力。难以预测的训练数据被赋予更多权重,而易于预测的实例被赋予更少的权重。模型一个接一个地顺序创建,每个模型更新训练实例上的权重,这些权重影响序列中下一个树所执行的学习。构建完所有树之后,将对新数据进行预测,并根据训练数据的准确性对每棵树的性能进行加权。
因为通过算法如此关注纠正错误,所以必须删除带有异常值的干净数据。
Adaboost 的 7 个优缺点

AdaBoost算法优点:
- 很好的利用了弱分类器进行级联;
- 可以将不同的分类算法作为弱分类器;
- AdaBoost具有很高的精度;
- 相对于bagging算法和Random Forest算法,AdaBoost充分考虑的每个分类器的权重;
Adaboost算法缺点:
- AdaBoost迭代次数也就是弱分类器数目不太好设定,可以使用交叉验证来进行确定;
- 数据不平衡导致分类精度下降;
- 训练比较耗时,每次重新选择当前分类器最好切分点;
百度百科和维基百科
Adaboost是一种迭代算法,其核心思想是针对同一个训练集训练不同的分类器(弱分类器),然后把这些弱分类器集合起来,构成一个更强的最终分类器(强分类器)。
AdaBoost是Adaptive Boosting的缩写,是由Yoav Freund和Robert Schapire制作的机器学习 元算法,他们因其工作而获得2003年哥德尔奖。它可以与许多其他类型的学习算法结合使用,以提高性能。其他学习算法(“弱学习者”)的输出被组合成加权和,该加权和表示提升分类器的最终输出。
AdaBoost在某种意义上是适应性的,即随后的弱学习者被调整为支持那些被先前分类器错误分类的实例。AdaBoost对噪声数据和异常值敏感。在某些问题中,它可能比其他学习算法更不容易受到过度拟合问题的影响。个体学习者可能很弱,但只要每个学习者的表现略好于随机猜测,最终的模型就可以证明可以融合到强大的学习者身上。
随机森林 – Random forest

随机森林是一种由决策树构成的集成算法,他在很多情况下都能有不错的表现。
本文将介绍随机森林的基本概念、4 个构造步骤、4 种方式的对比评测、10 个优缺点和 4 个应用方向。
什么是随机森林?
随机森林属于 集成学习 中的 Bagging(Bootstrap AGgregation 的简称) 方法。如果用图来表示他们之间的关系如下:
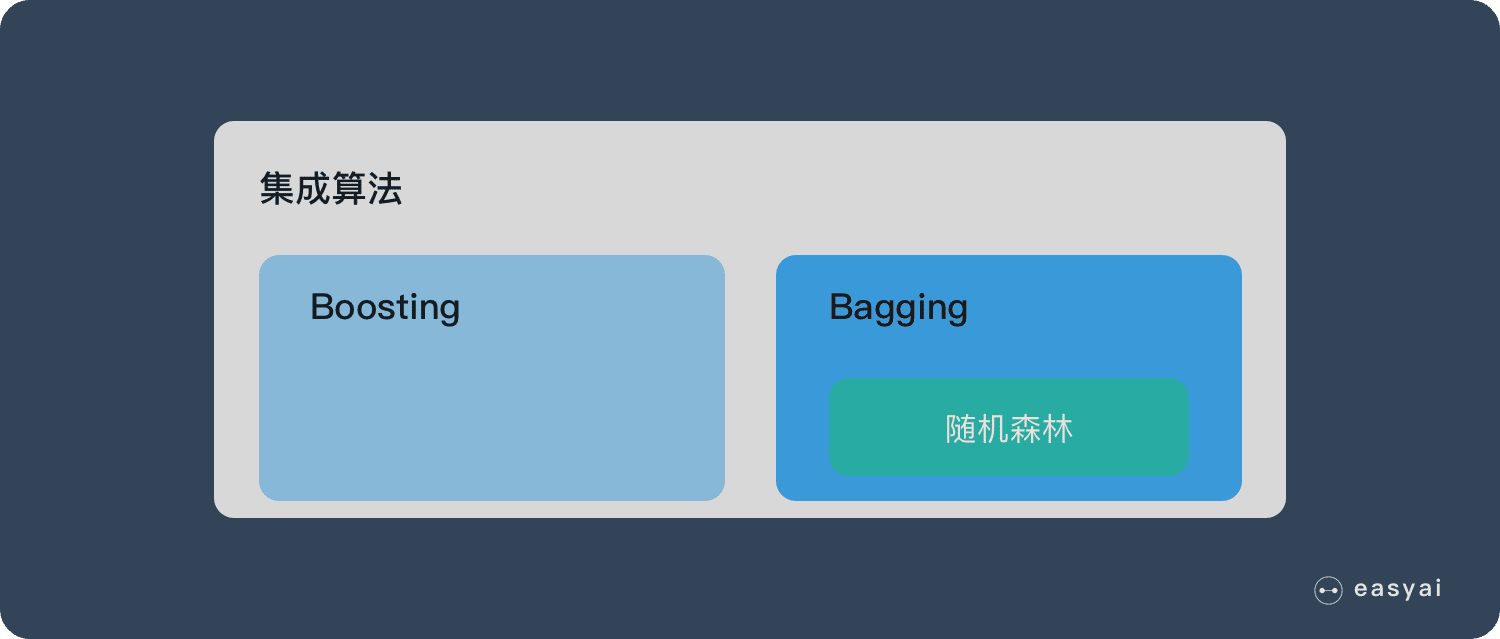
决策树 – Decision Tree
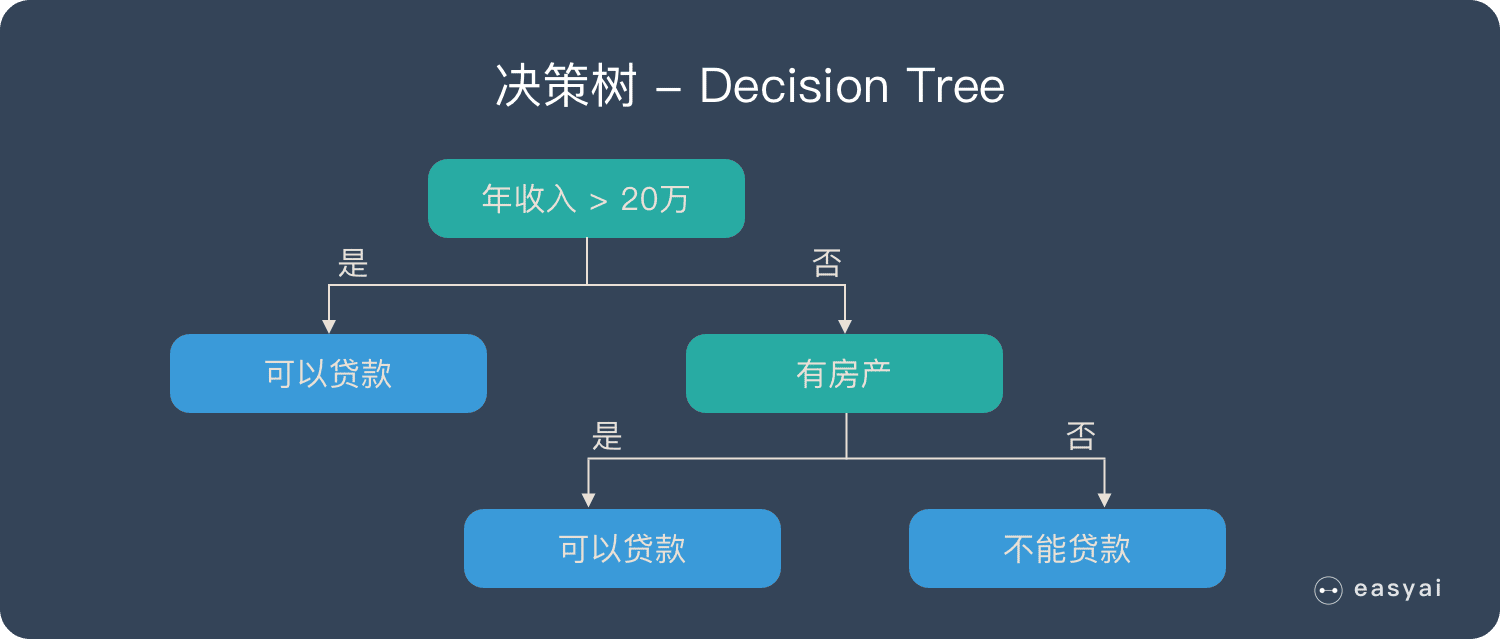
在解释随机森林前,需要先提一下决策树。决策树是一种很简单的算法,他的解释性强,也符合人类的直观思维。这是一种基于if-then-else规则的有监督学习算法,上面的图片可以直观的表达决策树的逻辑。
了解详情:《一文看懂决策树 – Decision tree(3个步骤+3种典型算法+10个优缺点)》
随机森林 – Random Forest | RF
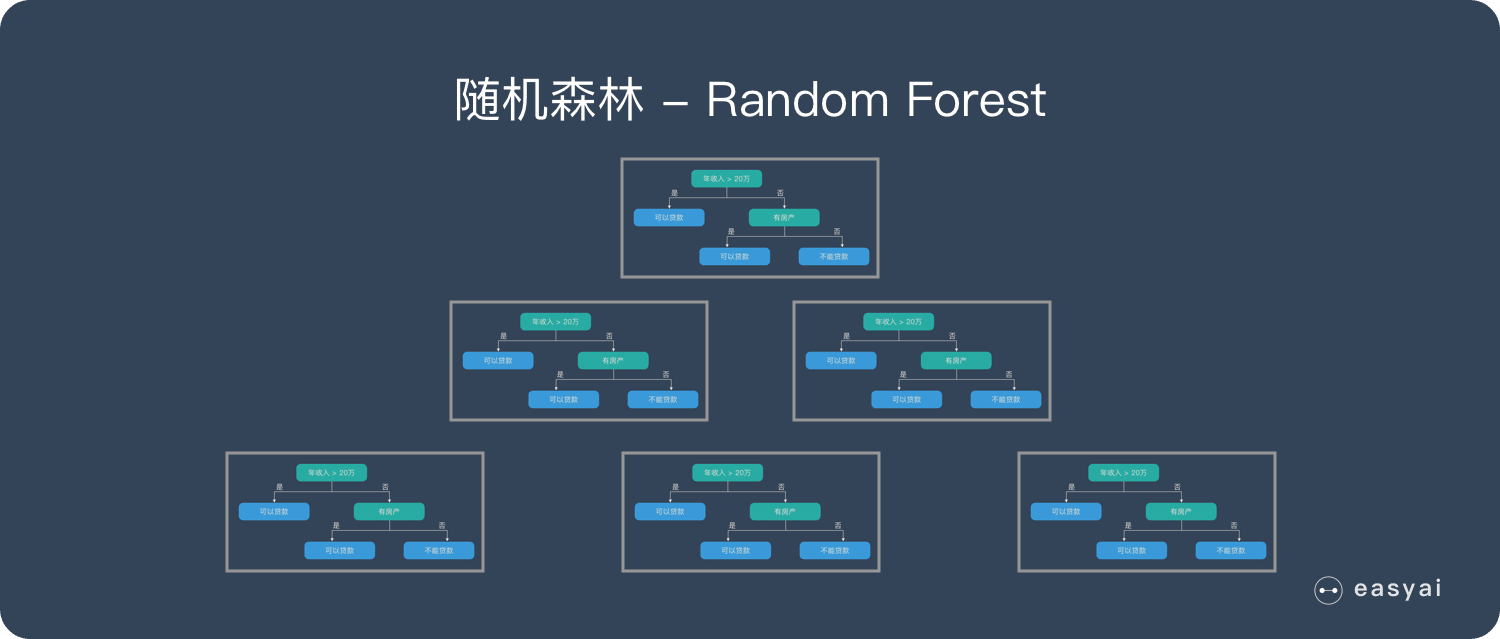
随机森林是由很多决策树构成的,不同决策树之间没有关联。
当我们进行分类任务时,新的输入样本进入,就让森林中的每一棵决策树分别进行判断和分类,每个决策树会得到一个自己的分类结果,决策树的分类结果中哪一个分类最多,那么随机森林就会把这个结果当做最终的结果。
构造随机森林的 4 个步骤

- 一个样本容量为N的样本,有放回的抽取N次,每次抽取1个,最终形成了N个样本。这选择好了的N个样本用来训练一个决策树,作为决策树根节点处的样本。
- 当每个样本有M个属性时,在决策树的每个节点需要分裂时,随机从这M个属性中选取出m个属性,满足条件m << M。然后从这m个属性中采用某种策略(比如说信息增益)来选择1个属性作为该节点的分裂属性。
- 决策树形成过程中每个节点都要按照步骤2来分裂(很容易理解,如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性,则该节点已经达到了叶子节点,无须继续分裂了)。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
- 按照步骤1~3建立大量的决策树,这样就构成了随机森林了。
随机森林的优缺点
优点
- 它可以出来很高维度(特征很多)的数据,并且不用降维,无需做特征选择
- 它可以判断特征的重要程度
- 可以判断出不同特征之间的相互影响
- 不容易过拟合
- 训练速度比较快,容易做成并行方法
- 实现起来比较简单
- 对于不平衡的数据集来说,它可以平衡误差。
- 如果有很大一部分的特征遗失,仍可以维持准确度。
缺点
- 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合。
- 对于有不同取值的属性的数据,取值划分较多的属性会对随机森林产生更大的影响,所以随机森林在这种数据上产出的属性权值是不可信的
随机森林 4 种实现方法对比测试
随机森林是常用的机器学习算法,既可以用于分类问题,也可用于回归问题。本文对 scikit-learn、Spark MLlib、DolphinDB、XGBoost 四个平台的随机森林算法实现进行对比测试。评价指标包括内存占用、运行速度和分类准确性。
测试结果如下:
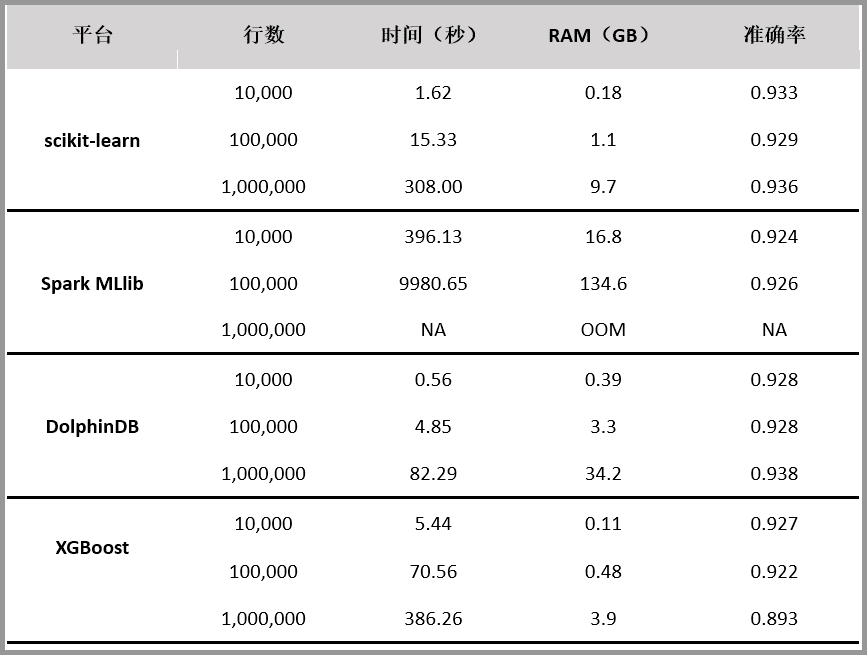
测试过程及说明忽略,感兴趣的可以查看原文《随机森林算法 4 种实现方法对比测试:DolphinDB 速度最快,XGBoost 表现最差》
随机森林的 4 个应用方向

随机森林可以在很多地方使用:
- 对离散值的分类
- 对连续值的回归
- 无监督学习聚类
- 异常点检测
百度百科+维基百科
在机器学习中,随机森林是一个包含多个决策树的分类器, 并且其输出的类别是由个别树输出的类别的众数而定。 Leo Breiman和Adele Cutler发展出推论出随机森林的算法。
随机森林或随机决策森林是用于分类,回归和其他任务的集成学习方法,其通过在训练时构建多个决策树并输出作为类的模式(分类)或平均预测(回归)的类来操作。个别树木。随机决策森林纠正决策树过度拟合其训练集的习惯。
扩展阅读
学习向量量化 – Learning vector quantization | LVQ
什么是学习向量量化?
K邻近算法的缺点是你需要坚持整个训练数据集。学习向量量化算法(或简称LVQ)是一种人工神经网络算法,允许您选择要挂起的训练实例数量,并准确了解这些实例应该是什么样子。
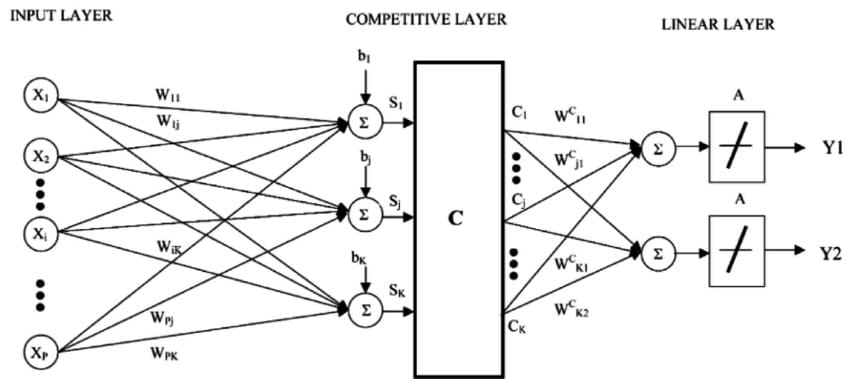
LVQ的表示是码本向量的集合。这些是在开始时随机选择的,并且适于在学习算法的多次迭代中最佳地总结训练数据集。在学习之后,可以使用码本向量来进行与K-Nearest Neighbors类似的预测。通过计算每个码本矢量和新数据实例之间的距离来找到最相似的邻居(最佳匹配码本矢量)。然后返回最佳匹配单元的类值或(回归情况下的实际值)作为预测。如果将数据重新缩放到相同范围(例如0到1之间),则可获得最佳结果。
如果您发现KNN在您的数据集上提供了良好的结果,请尝试使用LVQ来降低存储整个训练数据集的内存要求。
百度百科版本
学习向量量化(Learning Vector Quantization,简称LVQ)属于原型聚类,即试图找到一组原型向量来聚类,每个原型向量代表一个簇,将空间划分为若干个簇,从而对于任意的样本,可以将它划入到它距离最近的簇中,不同的是LVQ假设数据样本带有类别标记,因此可以利用这些类别标记来辅助聚类。
维基百科版本
LVQ可以被理解为人工神经网络的一个特例,更确切地说,它应用了一种赢家通吃的 Hebbian学习方法。它是自组织图(SOM)的前体,与神经气体有关,也与k-最近邻算法(k-NN)有关。LVQ由Teuvo Kohonen发明。
K邻近 – k-nearest neighbors | KNN
什么是 K邻近算法?
KNN算法非常简单且非常有效。KNN的模型表示是整个训练数据集。简单吧?
通过搜索K个最相似的实例(邻居)的整个训练集并总结那些K个实例的输出变量,对新数据点进行预测。对于回归问题,这可能是平均输出变量,对于分类问题,这可能是模式(或最常见)类值。
诀窍在于如何确定数据实例之间的相似性。如果您的属性具有相同的比例(例如,以英寸为单位),则最简单的技术是使用欧几里德距离,您可以根据每个输入变量之间的差异直接计算该数字。

KNN可能需要大量内存或空间来存储所有数据,但仅在需要预测时才进行计算(或学习),及时。您还可以随着时间的推移更新和策划您的训练实例,以保持预测准确。
距离或接近度的概念可以在非常高的维度(许多输入变量)中分解,这会对算法在您的问题上的性能产生负面影响。这被称为维度的诅咒。它建议您仅使用与预测输出变量最相关的输入变量。
K邻近算法的优缺点
优点
- 理论成熟,思想简单,既可以用来做分类也可以用来做回归;
- 可用于非线性分类;
- 训练时间复杂度为O(n);
- 对数据没有假设,准确度高,对outlier不敏感;
- KNN是一种在线技术,新数据可以直接加入数据集而不必进行重新训练;
- KNN理论简单,容易实现;
缺点
- 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少)效果差;
- 需要大量内存;
- 对于样本容量大的数据集计算量比较大(体现在距离计算上);
- 样本不平衡时,预测偏差比较大。如:某一类的样本比较少,而其它类样本比较多;
- KNN每一次分类都会重新进行一次全局运算;
- k值大小的选择没有理论选择最优,往往是结合K-折交叉验证得到最优k值选择;
百度百科版本
邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时,只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
维基百科版本
在模式识别中,k-最近邻算法(k -NN)是用于分类和回归的非参数方法。在这两种情况下,输入都包含特征空间中最近的k个训练样例。输出取决于k -NN是用于分类还是回归:
- 在k-NN分类中,输出是类成员资格。对象通过其邻居的多个投票进行分类,其中对象被分配给其k个最近邻居中最常见的类(k是正整数,通常是小整数)。如果k = 1,则简单地将对象分配给该单个最近邻居的类。
- 在k-NN回归中,输出是对象的属性值。该值是其k个最近邻居的值的平均值。
k -NN是一种基于实例的学习或懒惰学习,其中函数仅在本地近似,并且所有计算都推迟到分类。该ķ -NN算法是最简单的所有中机器学习算法。
线性判别分析 – Linear Discriminant Analysis | LDA
什么是线性判别分析?
逻辑回归是一种传统上仅限于两类分类问题的分类算法。如果您有两个以上的类,则线性判别分析算法是首选的线性分类技术。
LDA的代表非常简单。它包含数据的统计属性,为每个类计算。对于单个输入变量,这包括:
- 每个分类的平均值。
- 在所有类别中计算的方差。

通过计算每个类的判别值并对具有最大值的类进行预测来进行预测。该技术假设数据具有高斯分布(钟形曲线),因此最好事先从数据中删除异常值。它是分类预测建模问题的一种简单而强大的方法。
百度百科版本
线性判别分析(linear discriminant analysis,LDA)是对费舍尔的线性鉴别方法的归纳,这种方法使用统计学,模式识别和机器学习方法,试图找到两类物体或事件的特征的一个线性组合,以能够特征化或区分它们。所得的组合可用来作为一个线性分类器,或者,更常见的是,为后续的分类做降维处理。
维基百科版本
线性判别分析(LDA),正态判别分析(NDA)或判别函数分析是Fisher线性判别式的推广,这是一种用于统计,模式识别和机器学习的方法,用于找出表征或分离两个或两个特征的线性特征组合。更多类的对象或事件。得到的组合可以用作线性分类器,或者更常见地,用于在稍后分类之前降低维数。
人工智能和数据科学的十大角色
应用数据科学是一项高度跨学科的团队运动。透视的多样性很重要!事实上,观点和态度至少与教育和经验一样重要。如果您希望通过决策智能工程方法使数据变得有用,那么这就是我对团队发展的顺序的看法。
关于 TensorFlow,你应该知道的 9 个重点
TensorFlow 是一个强大的机器学习框架,本文介绍关于 TensorFlow 的9个特点,主要针对想要了解 TensorFlow 的技术人员和非技术人员。同时本文还包含了大量有用的资源,可以帮助大家更全面的了解和学习。
TF-IDF
什么是 TF-IDF 算法?
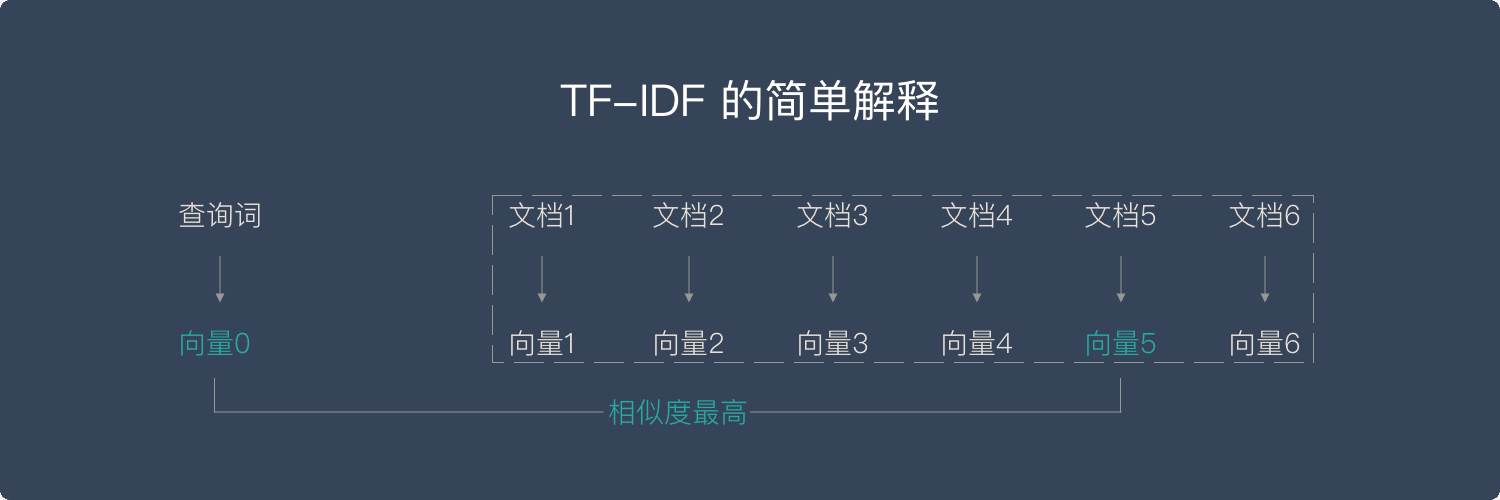
简单来说,向量空间模型就是希望把查询关键字和文档都表达成向量,然后利用向量之间的运算来进一步表达向量间的关系。比如,一个比较常用的运算就是计算查询关键字所对应的向量和文档所对应的向量之间的 “相关度”。
TF (Term Frequency)—— “单词频率”
意思就是说,我们计算一个查询关键字中某一个单词在目标文档中出现的次数。举例说来,如果我们要查询 “Car Insurance”,那么对于每一个文档,我们都计算“Car” 这个单词在其中出现了多少次,“Insurance”这个单词在其中出现了多少次。这个就是 TF 的计算方法。
TF 背后的隐含的假设是,查询关键字中的单词应该相对于其他单词更加重要,而文档的重要程度,也就是相关度,与单词在文档中出现的次数成正比。比如,“Car” 这个单词在文档 A 里出现了 5 次,而在文档 B 里出现了 20 次,那么 TF 计算就认为文档 B 可能更相关。
然而,信息检索工作者很快就发现,仅有 TF 不能比较完整地描述文档的相关度。因为语言的因素,有一些单词可能会比较自然地在很多文档中反复出现,比如英语中的 “The”、“An”、“But” 等等。这些词大多起到了链接语句的作用,是保持语言连贯不可或缺的部分。然而,如果我们要搜索 “How to Build A Car” 这个关键词,其中的 “How”、“To” 以及 “A” 都极可能在绝大多数的文档中出现,这个时候 TF 就无法帮助我们区分文档的相关度了。
IDF(Inverse Document Frequency)—— “逆文档频率”
就在这样的情况下应运而生。这里面的思路其实很简单,那就是我们需要去 “惩罚”(Penalize)那些出现在太多文档中的单词。
也就是说,真正携带 “相关” 信息的单词仅仅出现在相对比较少,有时候可能是极少数的文档里。这个信息,很容易用 “文档频率” 来计算,也就是,有多少文档涵盖了这个单词。很明显,如果有太多文档都涵盖了某个单词,这个单词也就越不重要,或者说是这个单词就越没有信息量。因此,我们需要对 TF 的值进行修正,而 IDF 的想法是用 DF 的倒数来进行修正。倒数的应用正好表达了这样的思想,DF 值越大越不重要。
TF-IDF 算法主要适用于英文,中文首先要分词,分词后要解决多词一义,以及一词多义问题,这两个问题通过简单的tf-idf方法不能很好的解决。于是就有了后来的词嵌入方法,用向量来表征一个词。
TF-IDF 的4个变种

变种1:通过对数函数避免 TF 线性增长
很多人注意到 TF 的值在原始的定义中没有任何上限。虽然我们一般认为一个文档包含查询关键词多次相对来说表达了某种相关度,但这样的关系很难说是线性的。拿我们刚才举过的关于 “Car Insurance” 的例子来说,文档 A 可能包含 “Car” 这个词 100 次,而文档 B 可能包含 200 次,是不是说文档 B 的相关度就是文档 A 的 2 倍呢?其实,很多人意识到,超过了某个阈值之后,这个 TF 也就没那么有区分度了。
用 Log,也就是对数函数,对 TF 进行变换,就是一个不让 TF 线性增长的技巧。具体来说,人们常常用 1+Log(TF) 这个值来代替原来的 TF 取值。在这样新的计算下,假设 “Car” 出现一次,新的值是 1,出现 100 次,新的值是 5.6,而出现 200 次,新的值是 6.3。很明显,这样的计算保持了一个平衡,既有区分度,但也不至于完全线性增长。
变种2:标准化解决长文档、短文档问题
经典的计算并没有考虑 “长文档” 和“短文档”的区别。一个文档 A 有 3,000 个单词,一个文档 B 有 250 个单词,很明显,即便 “Car” 在这两个文档中都同样出现过 20 次,也不能说这两个文档都同等相关。对 TF 进行 “标准化”(Normalization),特别是根据文档的最大 TF 值进行的标准化,成了另外一个比较常用的技巧。
变种3:对数函数处理 IDF
第三个常用的技巧,也是利用了对数函数进行变换的,是对 IDF 进行处理。相对于直接使用 IDF 来作为 “惩罚因素”,我们可以使用 N+1 然后除以 DF 作为一个新的 DF 的倒数,并且再在这个基础上通过一个对数变化。这里的 N 是所有文档的总数。这样做的好处就是,第一,使用了文档总数来做标准化,很类似上面提到的标准化的思路;第二,利用对数来达到非线性增长的目的。
变种4:查询词及文档向量标准化
还有一个重要的 TF-IDF 变种,则是对查询关键字向量,以及文档向量进行标准化,使得这些向量能够不受向量里有效元素多少的影响,也就是不同的文档可能有不同的长度。在线性代数里,可以把向量都标准化为一个单位向量的长度。这个时候再进行点积运算,就相当于在原来的向量上进行余弦相似度的运算。所以,另外一个角度利用这个规则就是直接在多数时候进行余弦相似度运算,以代替点积运算。
TF-IDF 的历史
把查询关键字(Query)和文档(Document)都转换成 “向量”,并且尝试用线性代数等数学工具来解决信息检索问题,这样的努力至少可以追溯到 20 世纪 70 年代。
1971 年,美国康奈尔大学教授杰拉德 · 索尔顿(Gerard Salton)发表了《SMART 检索系统:自动文档处理实验》(The SMART Retrieval System—Experiments in Automatic Document Processing)一文,文中首次提到了把查询关键字和文档都转换成 “向量”,并且给这些向量中的元素赋予不同的值。这篇论文中描述的 SMART 检索系统,特别是其中对 TF-IDF 及其变种的描述成了后续很多工业级系统的重要参考。
1972 年,英国的计算机科学家卡伦 · 琼斯(Karen Spärck Jones)在《从统计的观点看词的特殊性及其在文档检索中的应用》(A Statistical Interpretation of Term Specificity and Its Application in Retrieval) 一文中第一次详细地阐述了 IDF 的应用。其后卡伦又在《检索目录中的词赋值权重》(Index Term Weighting)一文中对 TF 和 IDF 的结合进行了论述。可以说,卡伦是第一位从理论上对 TF-IDF 进行完整论证的计算机科学家,因此后世也有很多人把 TF-IDF 的发明归结于卡伦。
杰拉德本人被认为是 “信息检索之父”。他 1927 年出生于德国的纽伦堡,并与 1950 年和 1952 年先后从纽约的布鲁克林学院获得数学学士和硕士学位,1958 年从哈佛大学获得应用数学博士学位,之后来到康奈尔大学参与组建计算机系。为了致敬杰拉德本人对现代信息检索技术的卓越贡献,现在,美国计算机协会 ACM(Association of Computing Machinery)每三年颁发一次“杰拉德 · 索尔顿奖”(Gerard Salton Award),用于表彰对信息检索技术有突出贡献的研究人员。卡伦 · 琼斯在 1988 年获得了第二届“杰拉德 · 索尔顿奖” 的殊荣。
备注:上面大部分内容摘抄自付费课程——《AI 技术内参》
百度百科+维基百科
TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。TF-IDF加权的各种形式常被搜索引擎应用,作为文件与用户查询之间相关程度的度量或评级。
除了TF-IDF以外,因特网上的搜索引擎还会使用基于链接分析的评级方法,以确定文件在搜寻结果中出现的顺序。
在信息检索中,tf-idf或TFIDF(术语频率 – 逆文档频率的缩写)是一种数字统计,旨在反映单词对集合或语料库中的文档的重要程度。它经常被用作搜索信息检索,文本挖掘和用户建模的加权因子。tf-idf值按比例增加一个单词出现在文档中的次数,并被包含该单词的语料库中的文档数量所抵消,这有助于调整某些单词在一般情况下更频繁出现的事实。Tf-idf是当今最受欢迎的术语加权方案之一; 数字图书馆中83%的基于文本的推荐系统使用tf-idf。
搜索引擎经常使用tf-idf加权方案的变体作为在给定用户查询的情况下对文档的相关性进行评分和排序的中心工具。tf-idf可以成功地用于各种主题领域的停用词过滤,包括文本摘要和分类。
