Author Archive

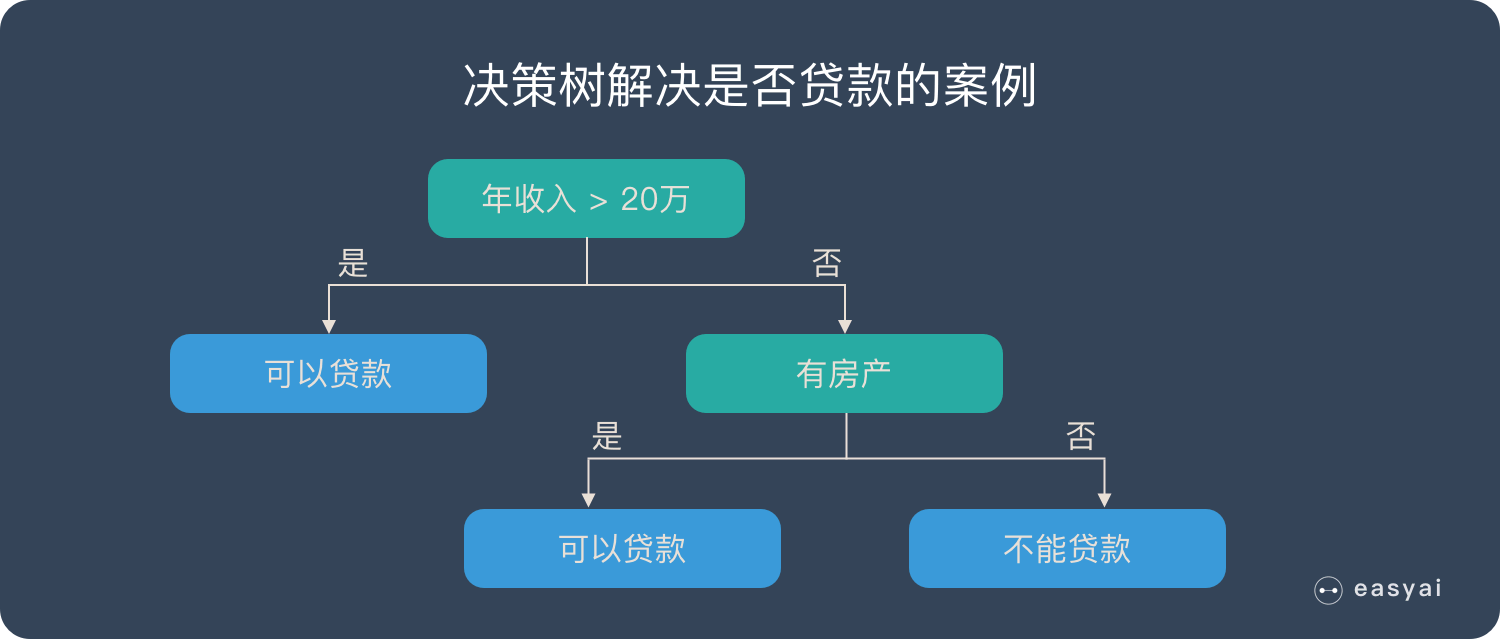
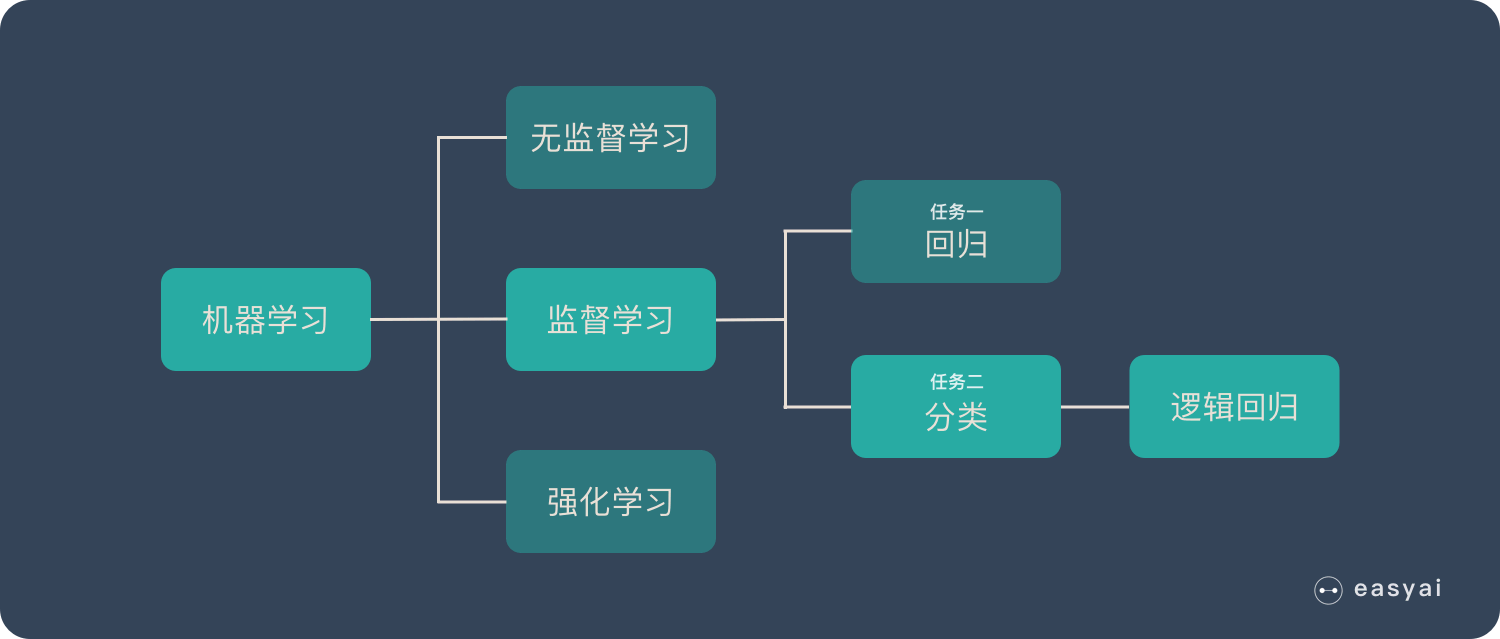
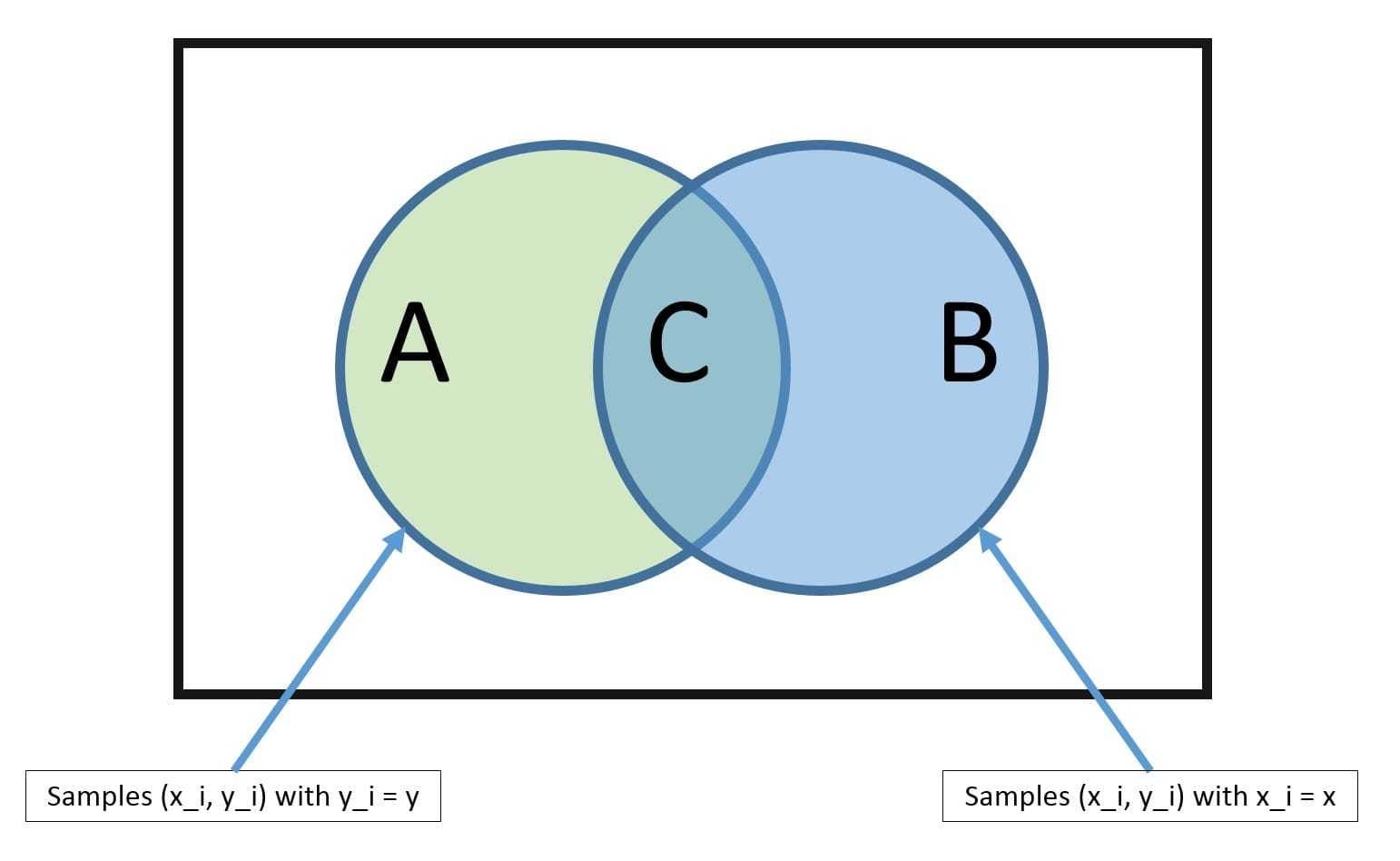
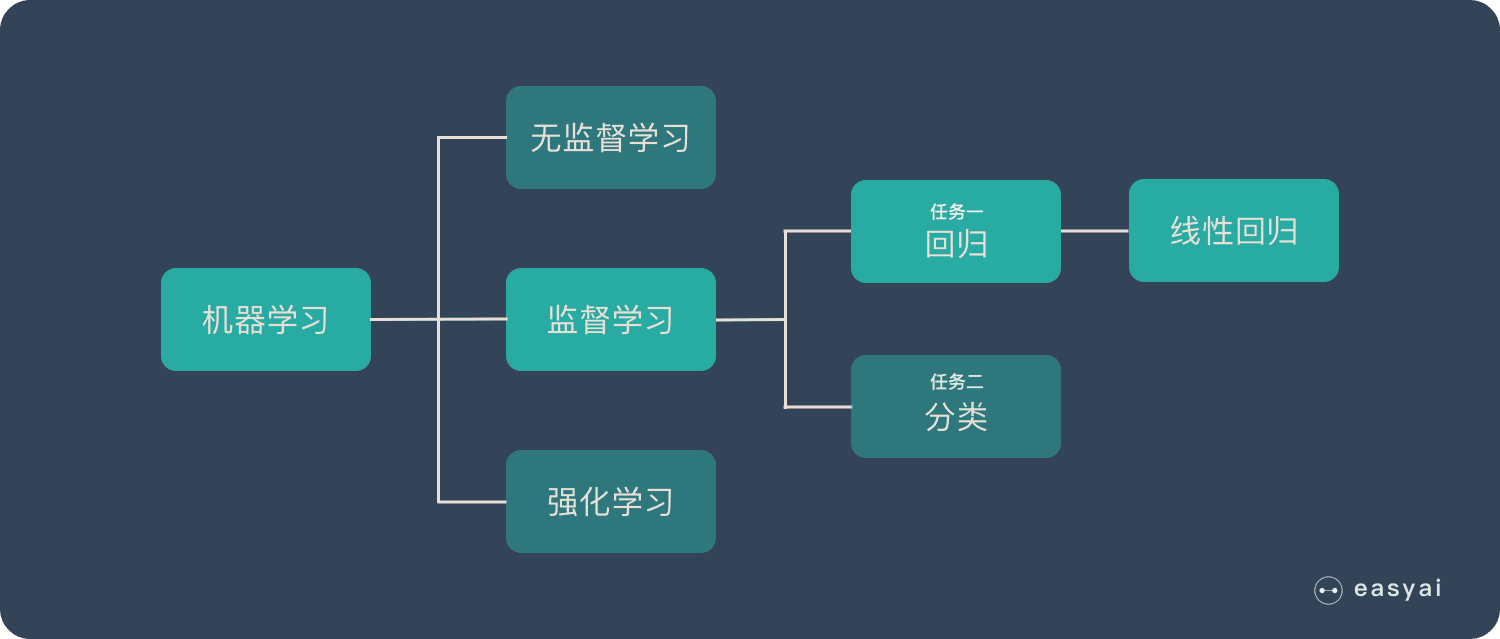
在机器学习中，我们讲了很多不同的算法。那些算法都是单打独斗的英雄。而集成学习就是将这些英雄组成团队。实现“3 个臭皮匠顶个诸葛亮”的效果。

本文将介绍集成学习的 2 种主要思路：bagging、boosting。

什么是集成学习？

集成学习归属于机器学习，他是一种「训练思路」，并不是某种具体的方法或者算法。

现实生活中，大家都知道「人多力量大」，「3 个臭皮匠顶个诸葛亮」。而集成学习的核心思路就是「人多力量大」，它并没有创造出新的算法，而是把已有的算法进行结合，从而得到更好的效果。

集成学习会挑选一些简单的基础模型进行组装，组装这些基础模型的思路主要有 2 种方法：

1. bagging（bootstrap aggregating的缩写，也称作“套袋法”）
2. boosting

Bagging

Bagging 的核心思路是——民主。

Bagging 的思路是所有基础模型都一致对待，每个基础模型手里都只有一票。然后使用民主投票的方式得到最终的结果。

大部分情况下，经过 bagging 得到的结果方差（variance）更小。

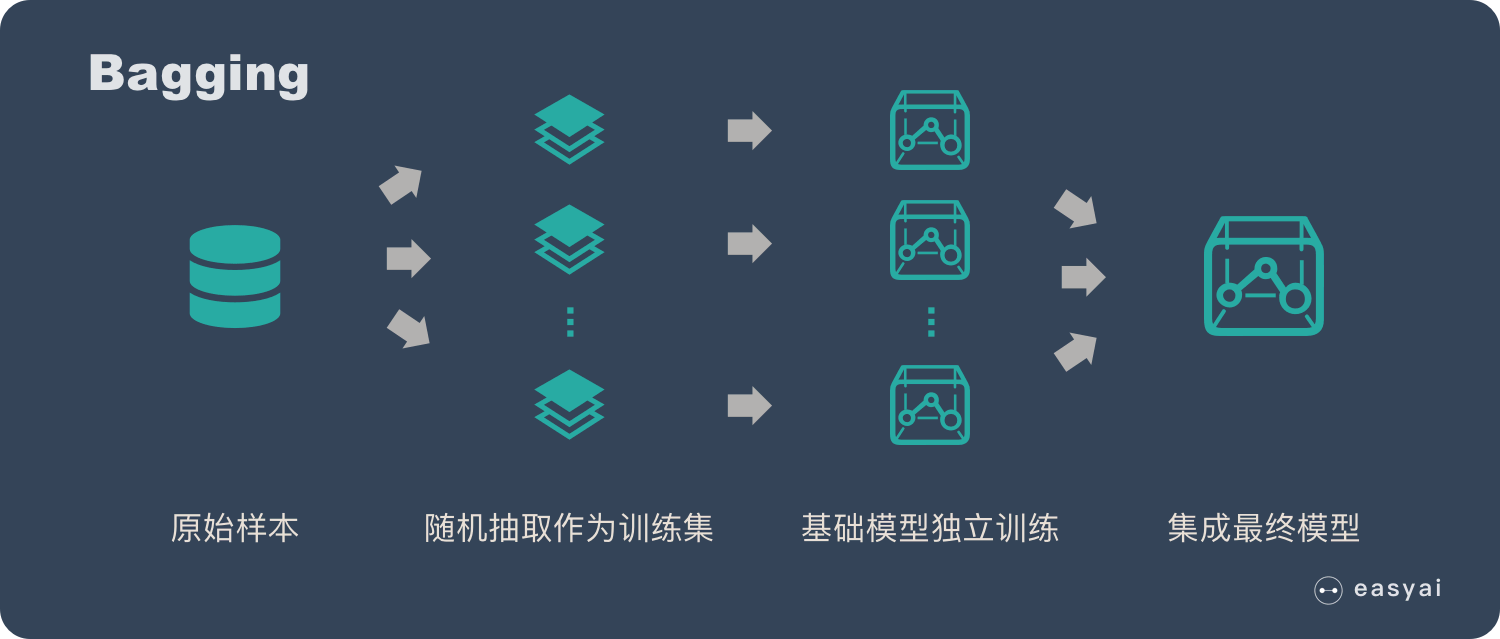
具体过程：

1. 从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）
2. 每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）
3. 对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

举例：

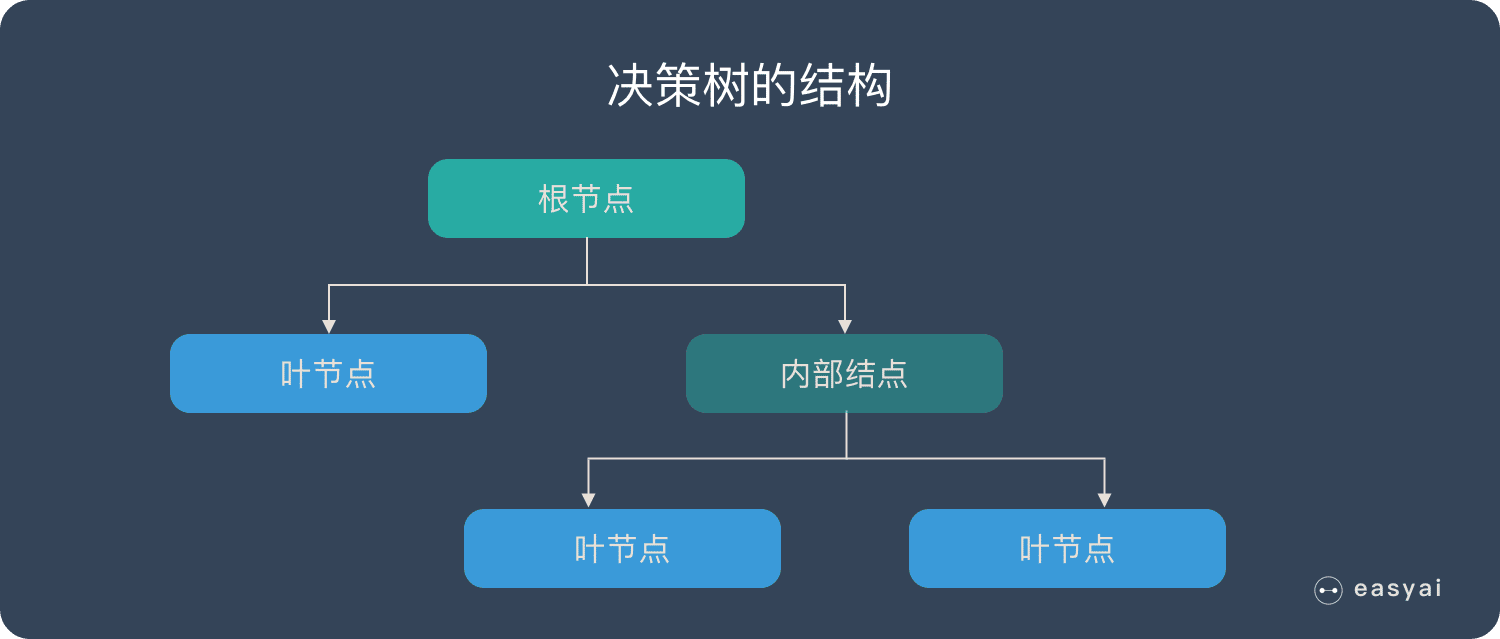
在 bagging 的方法中，最广为熟知的就是随机森林了：bagging + 决策树 = 随机森林

《一文看懂决策树（3个步骤+3种典型算法+10个优缺点）》

《一文看懂随机森林（4个步骤+4种方式评测+10个优缺点）》

Boosting

Boosting 的核心思路是——挑选精英。

Boosting 和 bagging 最本质的差别在于他对基础模型不是一致对待的，而是经过不停的考验和筛选来挑选出「精英」，然后给精英更多的投票权，表现不好的基础模型则给较少的投票权，然后综合所有人的投票得到最终结果。

大部分情况下，经过 boosting 得到的结果偏差（bias）更小。

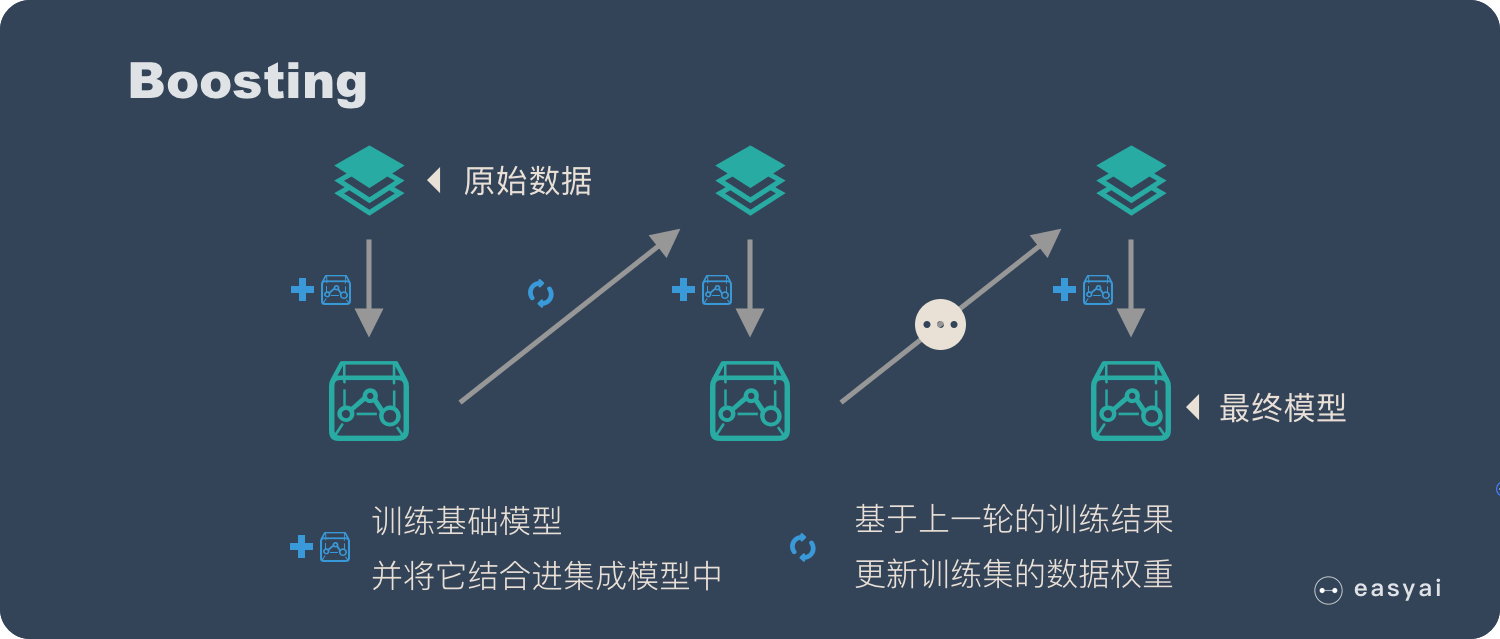
具体过程：

1. 通过加法模型将基础模型进行线性的组合。
2. 每一轮训练都提升那些错误率小的基础模型权重，同时减小错误率高的模型权重。
3. 在每一轮改变训练数据的权值或概率分布，通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。

举例：

在 boosting 的方法中，比较主流的有 Adaboost 和 Gradient boosting 。

《一文看懂 Adaboost 以及它的优缺点》

Bagging 和 Boosting 的4 点差别

样本选择上：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

样例权重：

Bagging：使用均匀取样，每个样例的权重相等

Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

预测函数：

Bagging：所有预测函数的权重相等。

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

并行计算：

Bagging：各个预测函数可以并行生成

Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

差别部分内容转自《Bagging和Boosting 概念及区别》

百度百科和维基百科

扩展阅读

【实践】5个集成学习最常用的方法