Author Archive

在機器學習中，我們講了很多不同的演算法。那些演算法都是單打獨鬥的英雄。而集成學習就是將這些英雄組成團隊。實現「3 個臭皮匠頂個諸葛亮」的效果。

本文將介紹集成學習的 2 種主要思路：bagging、boosting。

什麼是集成學習？

集成學習歸屬於機器學習，他是一種「訓練思路」，並不是某種具體的方法或者演算法。

現實生活中，大家都知道「人多力量大」，「3 個臭皮匠頂個諸葛亮」。而集成學習的核心思路就是「人多力量大」，它並沒有創造出新的演算法，而是把已有的演算法進行結合，從而得到更好的效果。

集成學習會挑選一些簡單的基礎模型進行組裝，組裝這些基礎模型的思路主要有 2 種方法：

1. bagging（bootstrap aggregating的縮寫，也稱作「套袋法」）
2. boosting

Bagging

Bagging 的核心思路是——民主。

Bagging 的思路是所有基礎模型都一致對待，每個基礎模型手裡都只有一票。然後使用民主投票的方式得到最終的結果。

大部分情況下，經過 bagging 得到的結果方差（variance）更小。

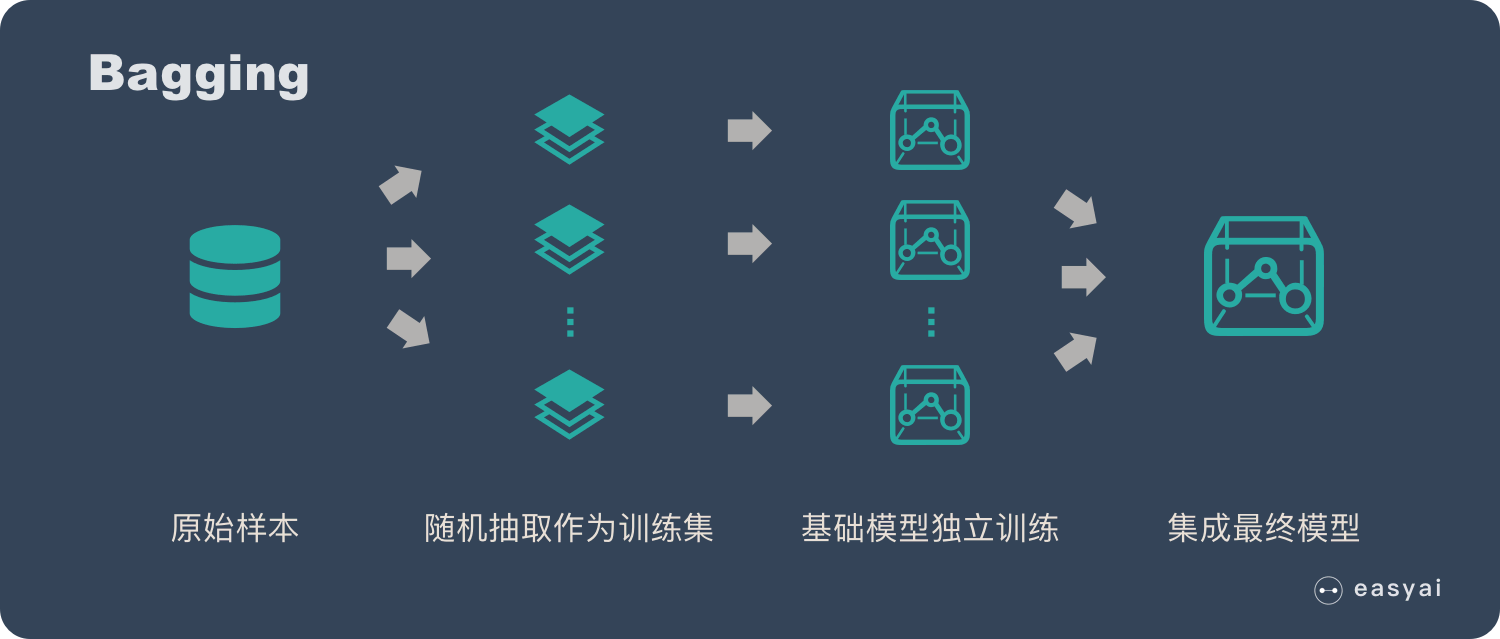
具體過程：

1. 從原始樣本集中抽取訓練集。每輪從原始樣本集中使用Bootstraping的方法抽取n個訓練樣本（在訓練集中，有些樣本可能被多次抽取到，而有些樣本可能一次都沒有被抽中）。共進行k輪抽取，得到k個訓練集。（k個訓練集之間是相互獨立的）
2. 每次使用一個訓練集得到一個模型，k個訓練集共得到k個模型。（註：這裡並沒有具體的分類演算法或回歸方法，我們可以根據具體問題採用不同的分類或回歸方法，如決策樹、感知器等）
3. 對分類問題：將上步得到的k個模型採用投票的方式得到分類結果；對回歸問題，計算上述模型的均值作為最後的結果。（所有模型的重要性相同）

舉例：

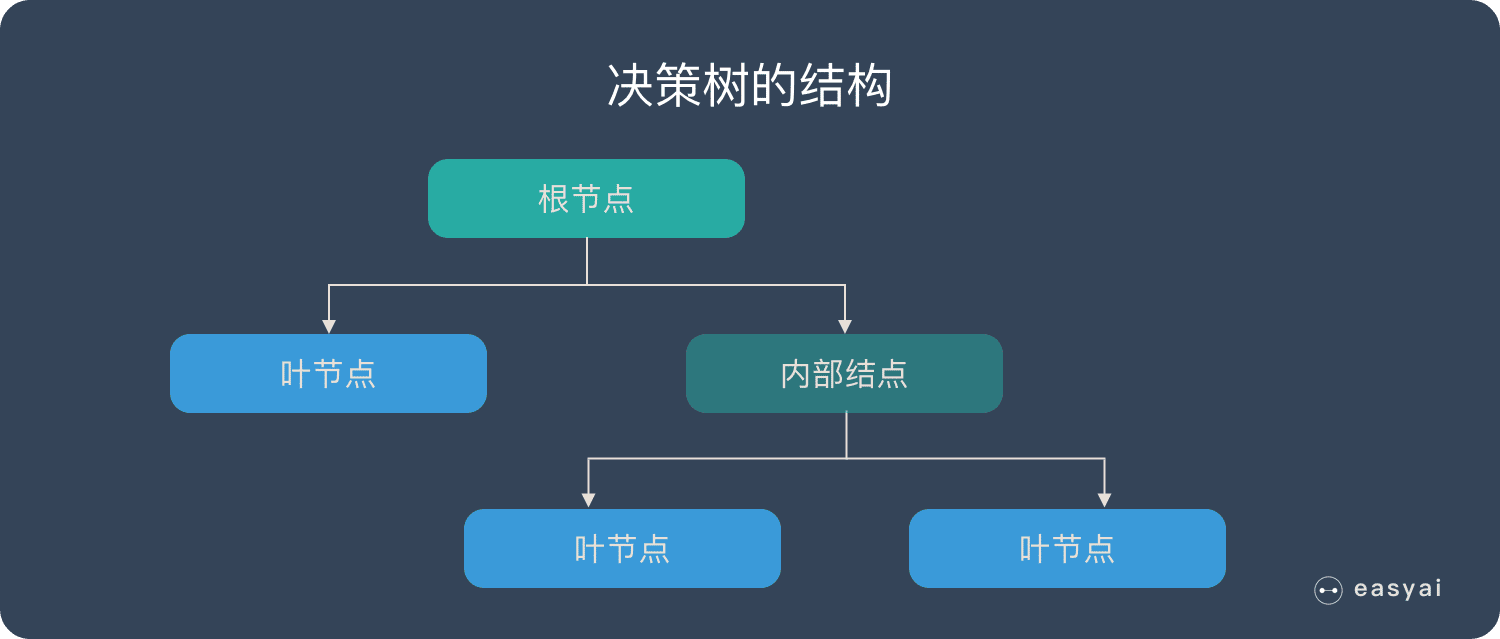
在 bagging 的方法中，最廣為熟知的就是隨機森林了：bagging + 決策樹 = 隨機森林

《一文看懂決策樹（3個步驟+3種典型演算法+10個優缺點）》

《一文看懂隨機森林（4個步驟+4種方式評測+10個優缺點）》

Boosting

Boosting 的核心思路是——挑選精英。

Boosting 和 bagging 最本質的差別在於他對基礎模型不是一致對待的，而是經過不停的考驗和篩選來挑選出「精英」，然後給精英更多的投票權，表現不好的基礎模型則給較少的投票權，然後綜合所有人的投票得到最終結果。

大部分情況下，經過 boosting 得到的結果偏差（bias）更小。

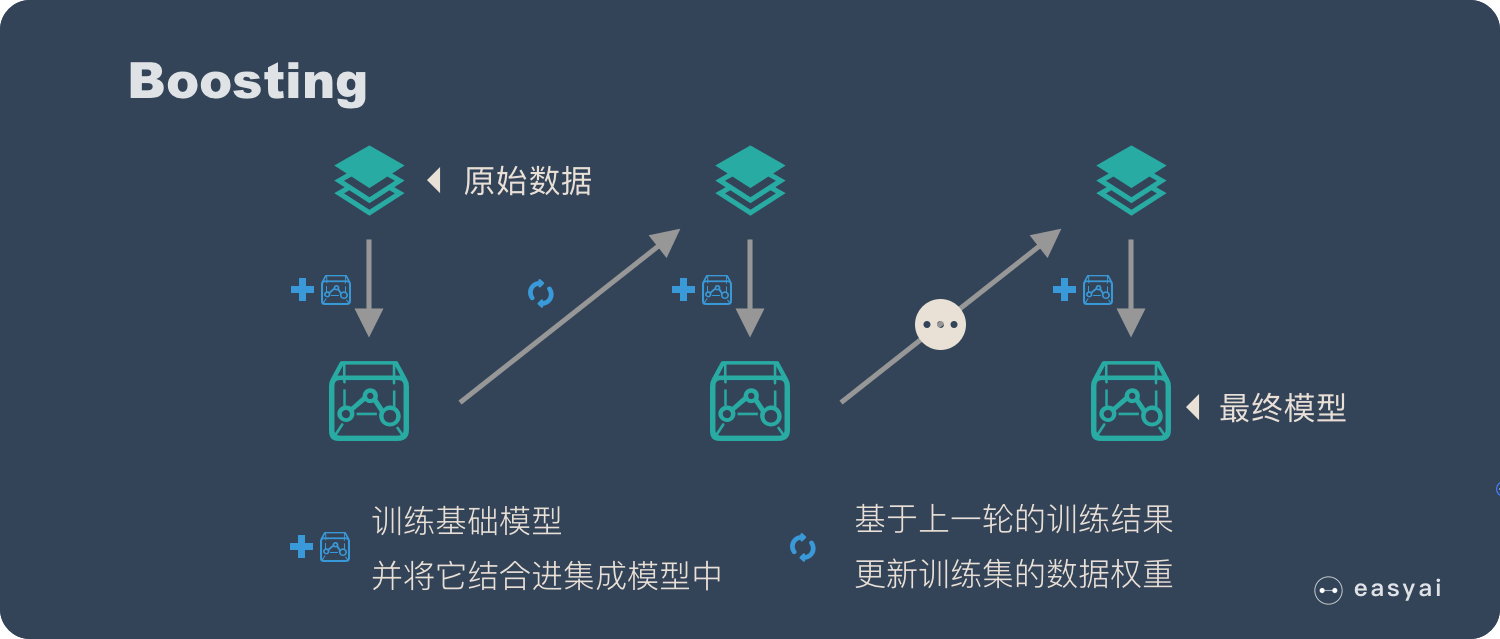
具體過程：

1. 通過加法模型將基礎模型進行線性的組合。
2. 每一輪訓練都提升那些錯誤率小的基礎模型權重，同時減小錯誤率高的模型權重。
3. 在每一輪改變訓練數據的權值或概率分布，通過提高那些在前一輪被弱分類器分錯樣例的權值，減小前一輪分對樣例的權值，來使得分類器對誤分的數據有較好的效果。

舉例：

在 boosting 的方法中，比較主流的有 Adaboost 和 Gradient boosting 。

《一文看懂 Adaboost 以及它的優缺點》

Bagging 和 Boosting 的4 點差別

樣本選擇上：

Bagging：訓練集是在原始集中有放回選取的，從原始集中選出的各輪訓練集之間是獨立的。

Boosting：每一輪的訓練集不變，只是訓練集中每個樣例在分類器中的權重發生變化。而權值是根據上一輪的分類結果進行調整。

樣例權重：

Bagging：使用均勻取樣，每個樣例的權重相等

Boosting：根據錯誤率不斷調整樣例的權值，錯誤率越大則權重越大。

預測函數：

Bagging：所有預測函數的權重相等。

Boosting：每個弱分類器都有相應的權重，對於分類誤差小的分類器會有更大的權重。

並行計算：

Bagging：各個預測函數可以並行生成

Boosting：各個預測函數只能順序生成，因為後一個模型參數需要前一輪模型的結果。

差別部分內容轉自《Bagging和Boosting 概念及區別》

百度百科和維基百科

擴展閱讀

【實踐】5個集成學習最常用的方法