想要快速區分標記的數據時,我們很容易忽略無監督學習。無監督的機器學習本身就非常強大,而聚類是迄今為止這類問題中最常見的方式。
這是三種最流行的聚類方法的快速破解,以及哪種類型的情況最適合。聚類與監督問題有一點共同點就是沒有銀彈; 每個演算法都有其時間和地點,具體取決於您要完成的任務。這應該給你一些直覺,就像何時使用它們一樣,只有一點點數學。
分層聚類
想像一下,你有集群的一些數量ķ你有興趣在尋找。您所知道的是,您可以將數據集分解為頂級的許多不同組,但您可能也對組內的組或這些組內的組感興趣。為了獲得這種結構,我們使用層次聚類。
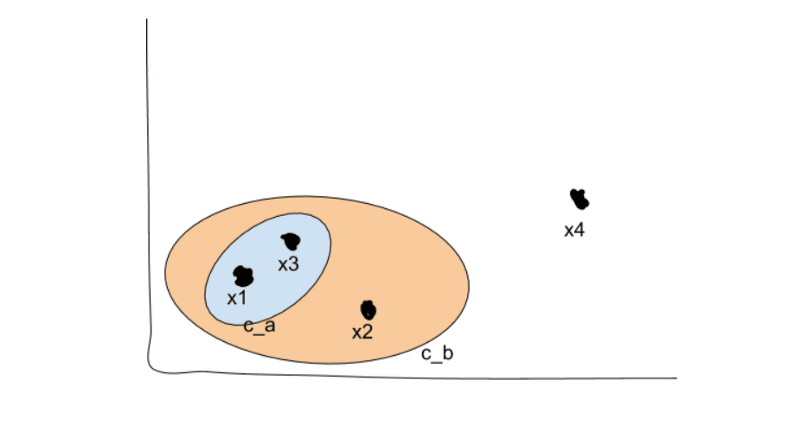
我們從n個不同的點和我們想要發現的k個不同的簇開始; 就我們而言,n = 4,k = 2。
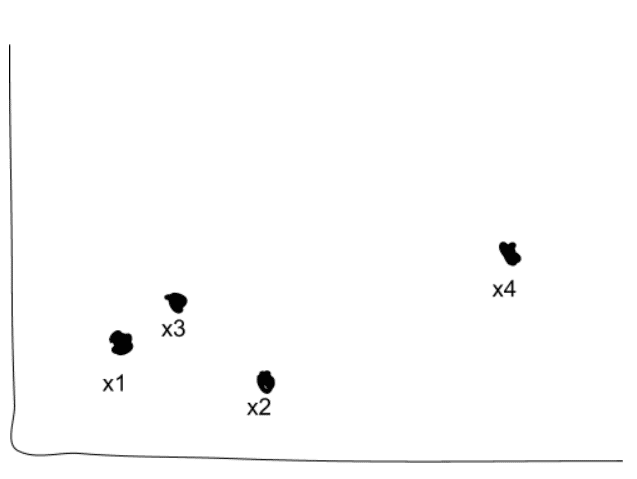
首先將每個點視為自己的集群。

然後,我們開始將每個單點集群合併為更大的集群,使用最接近的集群。我們找到距離成對距離矩陣的最小距離 – 這只是每個群集與其他群集距離的表格。
這被初始化為每個點之間的歐幾里德距離,但在此之後,我們切換到測量簇距離的各種不同方式之一。如果您有興趣了解有關這些技術的更多信息,請查看單鏈路聚類,完整鏈路聚類,clique邊距和Ward’s方法。
無論如何,我們開始合併最接近的集群。假設我們知道x1和x3最接近。然後我們將這兩個合併到一個新的集群中,ca。
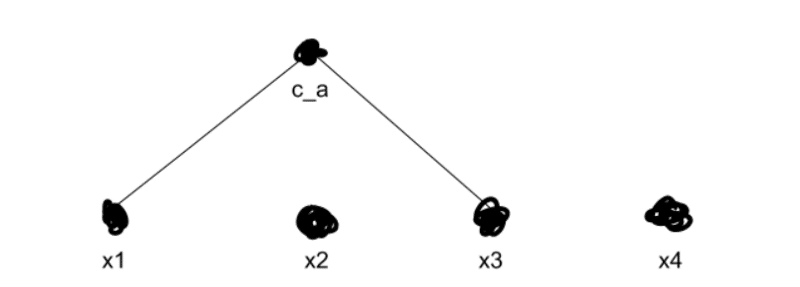
我們現在使用我們偏愛上述抓鬥的方法重新計算每個其他群集的距離。然後我們重複,一遍又一遍地合併我們的聚類,直到我們得到k個頂級聚類 – 在我們的例子中,兩個聚類。假設我們發現x2更接近於ca而不是x4。
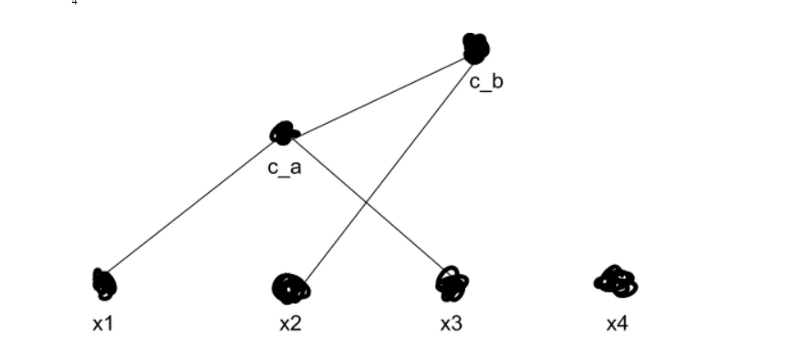
我們現在有兩個頂級集群,cb和x4(請記住,每個點都作為自己的集群開始)。我們現在可以搜索我們創建的樹結構來搜索子集群,在我們原來的2-D視圖中看起來像這樣:
基於密度的聚類
分層聚類有助於理解數據中的任何隱藏結構,但它有一個主要的缺陷。在上面顯示的版本中,我們假設每個數據點都是相關的 – 在現實世界中幾乎不是這種情況。
基於密度的聚類方法提供安全閥。我們不會假設每個點都是某個集群的一部分,而是只關注緊密堆積的點並假設其他所有點都是雜訊。
該方法需要兩個參數:半徑ε和鄰域密度Σ。對於每個點,我們計算Neps(x) – 距離x最多ε的點數。如果Neps(x)≥Σ,不計算x,那麼x被認為是核心點。如果一個點不是核心點,但它是核心點鄰域的成員,那麼它被認為是邊界點。其他一切都被認為是噪音。
基於密度的聚類的最常見且實際上是表演性實現之一是基於密度的具有雜訊的應用的空間聚類,更好地稱為DBSCAN。DBSCAN的工作原理是跨不同的核心點運行連接組件演算法。如果兩個核心點共享邊界點,或者核心點是另一個核心點鄰域中的邊界點,那麼它們就是相同連通組件的一部分,這組成了一個集群。
假設我們有一個相對較小的ε和一個相當大的Σ。我們可能會結束這樣的集群:
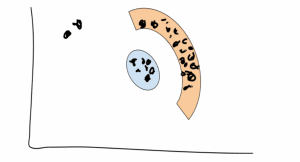
看到?那兩個孤獨的點距離兩個星團很遠,而且他們真的沒有什麼意義 – 所以它們只是噪音。
請注意,我們也能夠以這種方式發現非凸簇(參見橙色弧)。很簡約!
我們不需要為基於密度的聚類指定一些我們感興趣的聚類 – 它將根據您的ε和Σ自動發現一些聚類。當您希望所有群集具有相似的密度時,這尤其有用。
K-Means聚類
分層聚類擅長於發現數據中的嵌入式結構,而基於密度的方法在尋找具有相似密度的未知數量的聚類方面表現優異。但是,兩者都無法在整個數據集中找到「共識」。分層聚類可以將看起來很接近的聚類放在一起,但不考慮其他點的信息。基於密度的方法僅查看附近點的小鄰域,同樣無法考慮完整數據集。
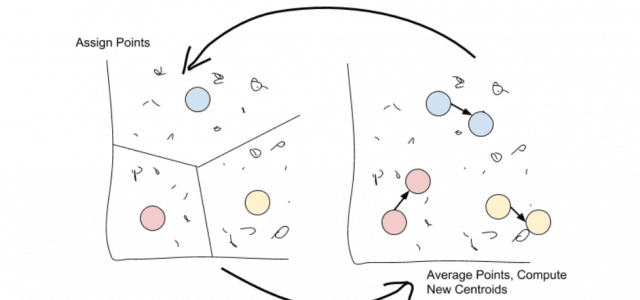
這就是K-means聚類的用武之地。從某種意義上說,K-means考慮數據集中的每個點,並使用該信息在一系列迭代中進化聚類。
K-means通過選擇k個中心點或裝置來工作,因此選擇K-Means。然後將這些均值用作其群集的質心:任何最接近給定均值的點都將分配給該均值的群集。
分配完所有點後,移動每個群集並獲取其包含的所有點的平均值。這個新的「平均」點是集群的新均值。
只需重複這兩個步驟,直到點分配停止變化!
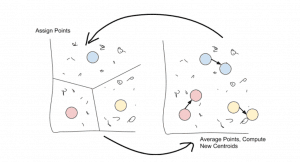
一旦點分配停止改變,該演算法就會被收斂。
我們現在將擁有k個不同的簇,每個簇的質心更接近其簇中的每個點,而不是任何其他質心。再次計算質心不會改變分配,所以我們停下來。這就是K-means的全部內容,但它是一種非常強大的方法,可以在考慮整個數據集時查找已知數量的聚類。
有很多方法可以初始化你的資金。Forgy方法從數據中隨機選擇k個隨機觀測值並將其作為起點。隨機分區方法將數據集中的每個點分配給隨機簇,然後根據這些點計算質心並恢復演算法。
雖然K-means是一個NP難問題,但是啟發式方法能夠在多項式時間內找到對全局最優的適當近似,並且能夠有效地處理大數據集,在某些情況下使其成為層次聚類的可靠選擇。
聚類是一個奇怪的世界,擁有更奇怪的技術集合。這三種方法只是最流行的一些方法,但它們可以幫助您在數據中發現未知分組。集群在探索性數據分析,查找其他分析的初始化點以及部署非常簡單方面非常有用。明智地使用群集可以為您的數據提供令人驚訝的見解。考慮一下你腰帶上的另一個缺口。
本文轉自medium,原文地址



Comments