機器學習全靠調參?這個思路已經過時了。
谷歌大腦團隊發布了一項新研究:
只靠神經網路架構搜索出的網路,不訓練,不調參,就能直接執行任務。
這樣的網路叫做WANN,權重不可知神經網路。
它在MNIST數字分類任務上,未經訓練和權重調整,就達到了92%的準確率,和訓練後的線性分類器表現相當。
除了監督學習,WANN還能勝任許多強化學習任務。
團隊成員之一的大佬David Ha,把成果發上了推特,已經獲得了1300多贊:
那麼,先來看看效果吧。
效果
谷歌大腦用WANN處理了3種強化學習任務。
(給每一組神經元,共享同一個權重。)
第一項任務,Cart-Pole Swing-Up。
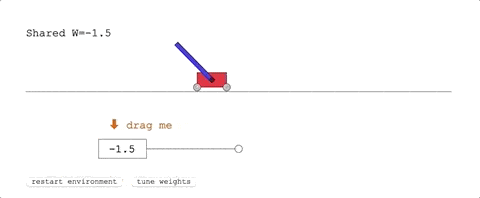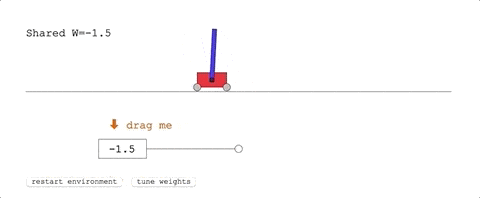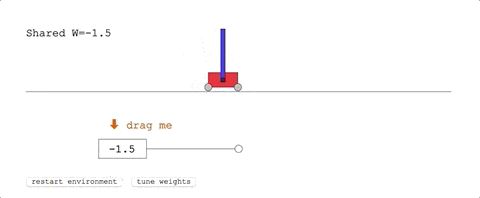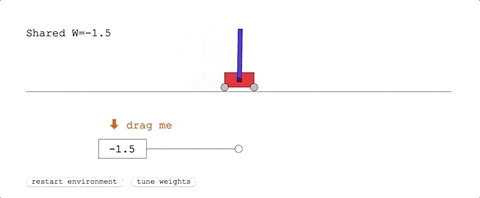
這是經典的控制任務,一條滑軌,一台小車,車上一根杆子。
小車在滑軌的範圍里跑,要把杆子從自然下垂的狀態搖上來,保持在直立的位置不掉下來。
(這個任務比單純的Cart-Pole要難一些:
Cart-Pole杆子的初始位置就是向上直立,不需要小車把它搖上來,只要保持就可以。)
難度體現在,沒有辦法用線性控制器 (Linear Controller) 來解決。每一個時間步的獎勵,都是基於小車到滑軌一頭的距離,以及杆子擺動的角度。
WANN的最佳網路 (Champion Network) 長這樣:
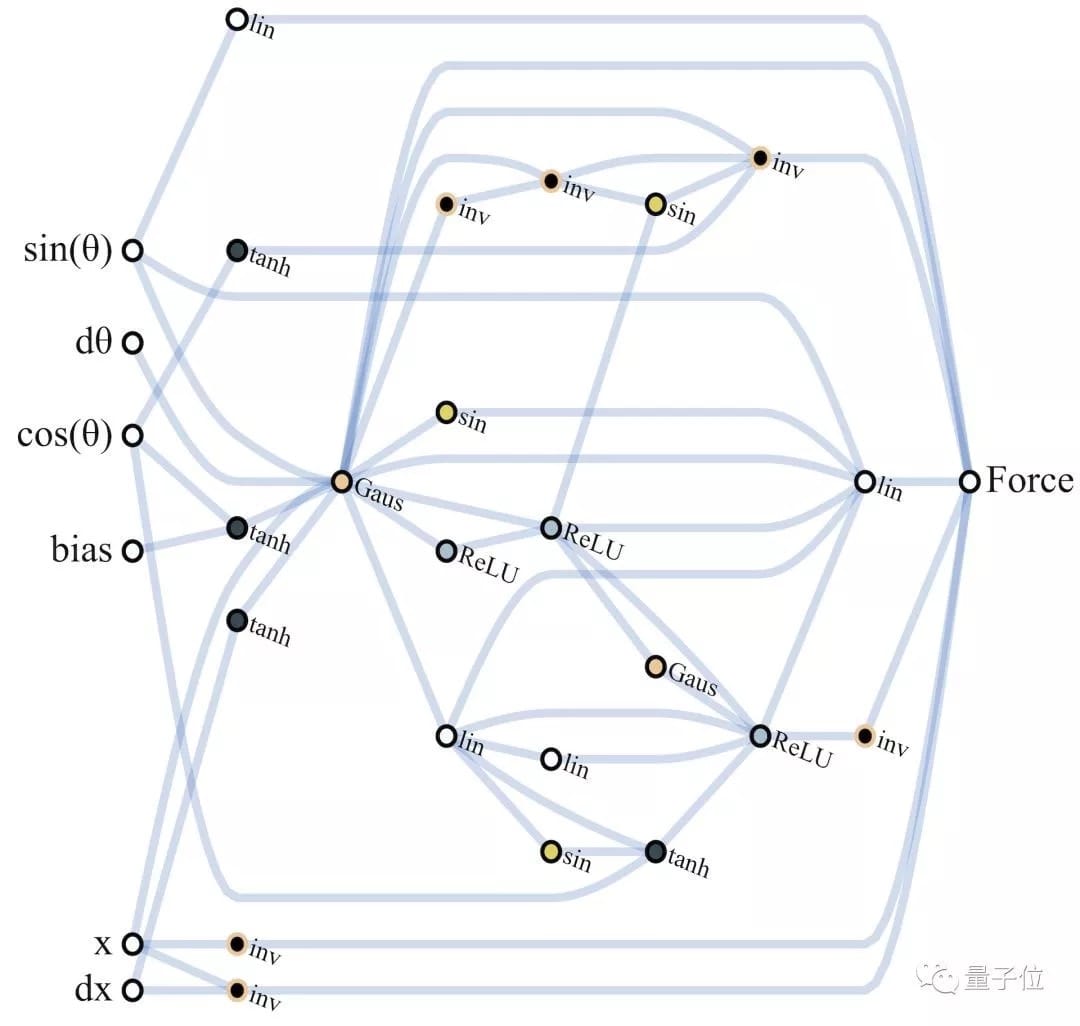
它在沒有訓練的狀態下,已經表現優異:

表現最好的共享權重,給了團隊十分滿意的結果:只用幾次擺動便達到了平衡狀態。
第二項任務,Bipedal Waker-v2。

一隻兩足「生物」,要在隨機生成的道路上往前走,越過凸起,跨過陷坑。獎勵多少,就看它從出發到掛掉走了多長的路,以及電機扭矩的成本 (為了鼓勵高效運動) 。
每條腿的運動,都是由一個髖關節、和一個膝關節來控制的。有24個輸入,會指導它的運動:包括「激光雷達」探測的前方地形數據,本體感受到的關節運動速度等等。
比起第一項任務中的低維輸入,這裡可能的網路連接就更多樣了:
所以,需要WANN對從輸入到輸出的布線方式,有所選擇。
這個高維任務,WANN也優質完成了。
你看,這是搜索出的最佳架構,比剛才的低維任務複雜了許多:
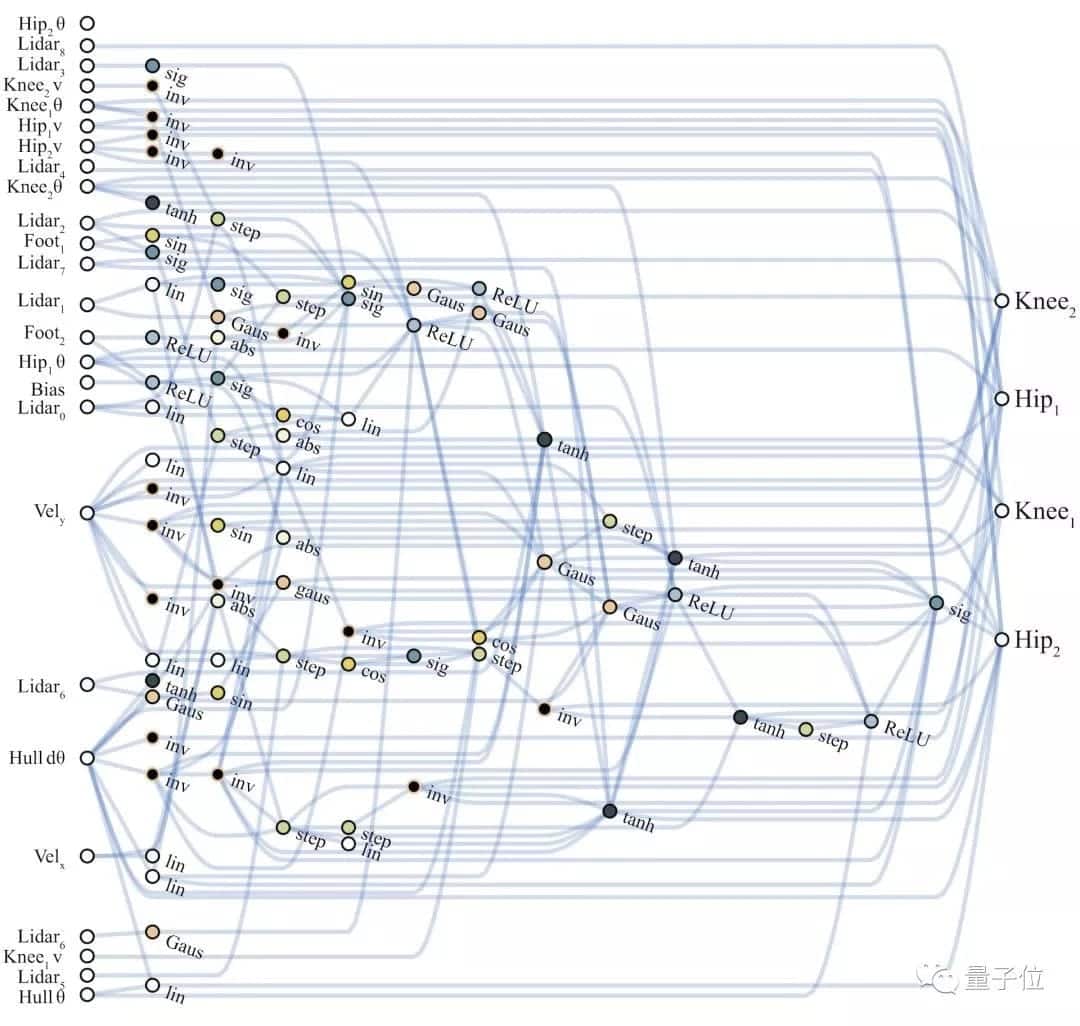
它在-1.5的權重下奔跑,長這樣:

第三項任務,CarRacing-v0。
這是一個自上而下的 (Top-Down) 、像素環境里的賽車遊戲。
一輛車,由三個連續命令來控制:油門、轉向、制動。目標是在規定的時間裡,經過儘可能多的磚塊。賽道是隨機生成的。
研究人員把解釋每個像素 (Pixel Interpretation) 的工作交給了一個預訓練的變分自編碼器 (VAE) ,它可以把像素表徵壓縮到16個潛在維度。
這16維就是網路輸入的維度。學到的特徵是用來檢測WANN學習抽象關聯 (Abstract Associations) 的能力,而不是編碼不同輸入之間顯式的幾何關係。
這是WANN最佳網路,在-1.4共享權重下、未經訓練的賽車成果:

雖然路走得有些蜿蜒,但很少偏離跑到。
而把最佳網路微調一下,不用訓練,便更加順滑了:

總結一下,在簡單程度和模塊化程度上,第二、三項任務都表現得優秀,兩足控制器只用了25個可能輸入中的17個,忽略了許多LIDAR感測器和膝關節的速度。
WANN架構不止能在不訓練單個權重的情況下完成任務,而且只用了210個網路連接 (Connections) ,比當前State-of-the-Art模型用到的2804個連接,少了一個數量級。
做完強化學習,團隊又瞄準了MNIST,把WANN拓展到了監督學習的分類任務上。
一個普通的網路,在參數隨機初始化的情況下,MNIST上面的準確率可能只有10%左右。
而新方法搜索到的網路架構WANN,用隨機權重去跑,準確率已經超過了80%;
如果像剛剛提到的那樣,餵給它多個權值的合集,準確率就達到了91.6%。
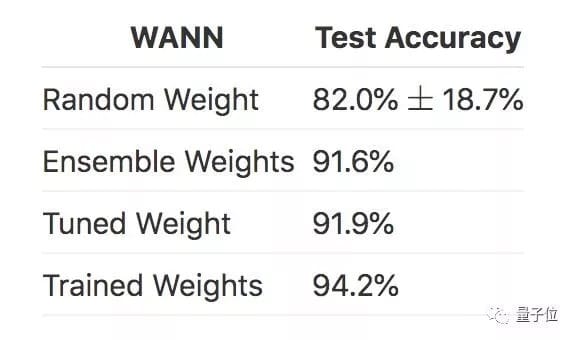
對比一下,經過微調的權重,帶來的準確率是91.9%,訓練過的權重,可以帶來94.2%的準確率。
再對比一下,擁有幾千個權重的線性分類器:

也只是和WANN完全沒訓練、沒微調、僅僅餵食了一些隨機權重時的準確率相當。
論文里強調,MINST手寫數字分類是高維分類任務。WANN表現得非常出色。
並且沒有哪個權值,顯得比其他值更優秀,大家表現得十分均衡:所以隨機權重是可行的。

不過,每個不同的權重形成的不同網路,有各自擅長分辨的數字,所以可以把一個擁有多個權值的WANN,用作一個自給自足的合集 (Self-Contained Ensemble) 。
實現原理
不訓練權重參數獲得極高準確度,WANN是如何做到的呢?
神經網路不僅有權重偏置這些參數,網路的拓撲結構、激活函數的選擇都會影響最終結果。

谷歌大腦的研究人員在論文開頭就提出質疑:神經網路的權重參數與其架構相比有多重要?在沒有學習任何權重參數的情況下,神經網路架構可以在多大程度上影響給定任務的解決方案。
為此,研究人員提出了一種神經網路架構的搜索方法,無需訓練權重找到執行強化學習任務的最小神經網路架構。
谷歌研究人員還把這種方法用在監督學習領域,僅使用隨機權重,就能在MNIST上實現就比隨機猜測高得多的準確率。
論文從架構搜索、貝葉斯神經網路、演算法資訊理論、網路剪枝、神經科學這些理論中獲得啟發。
為了生成WANN,必須將權重對網路的影響最小化,用權重隨機採樣可以保證最終的網路是架構優化的產物,但是在高維空間進行權重隨機採樣的難度太大。
研究人員採取了「簡單粗暴」的方法,對所有權重強制進行權重共享(weight-sharing),讓權重值的數量減少到一個。這種高效的近似可以推動對更好架構的搜索。
操作步驟
解決了權重初始化的問題,接下來的問題就是如何收搜索權重不可知神經網路。它分為四個步驟:

1、創建初始的最小神經網路拓撲群。
2、通過多個rollout評估每個網路,並對每個rollout分配不同的共享權重值。
3、根據性能和複雜程度對網路進行排序。
4、根據排名最高的網路拓撲來創建新的群,通過競爭結果進行概率性的選擇。
然後,演算法從第2步開始重複,在連續迭代中,產生複雜度逐漸增加的權重不可知拓撲(weight agnostic topologies )。
拓撲搜索
用於搜索神經網路拓撲的操作受到神經進化演算法(NEAT)的啟發。在NEAT中,拓撲和權重值同時優化,研究人員忽略權重,只進行拓撲搜索操作。

上圖展示了網路拓撲空間搜索的具體操作:
一開始網路上是最左側的最小拓撲結構,僅有部分輸入和輸出是相連的。
然後,網路按以下三種方式進行更改:
1、插入節點:拆分現有連接插入新節點。
2、添加連接:連接兩個之前未連接的節點,添加新連接。
3、更改激活函數:重新分配隱藏節點的激活函數。
圖的最右側展示了權重在[2,2]取值範圍內可能的激活函數,如線性函數、階躍函數、正弦餘弦函數、ReLU等等。
權重依然重要
WANN與傳統的固定拓撲網路相比,可以使用單個的隨機共享權重也能獲得更好的結果。

雖然WANN在多項任務中取得了最佳結果,但WANN並不完全獨立於權重值,當隨機分配單個權重值時,有時也會失敗。
WANN通過編碼輸入和輸出之間的關係起作用,雖然權重的大小的重要性並不高,但它們的一致性,尤其是符號的一致性才是關鍵。
隨機共享權重的另一個好處是,調整單個參數的影響變得不重要,無需使用基於梯度的方法。
強化學習任務中的結果讓作者考慮推廣WANN方法的應用範圍。他們又測試了WANN在圖像分類基礎任務MNIST上的表現,結果在權重接近0時效果不佳。

有Reddit網友質疑WANN的結果,對於隨機權重接近於0的情況,該網路的性能並不好,先強化學習實驗中的具體表現就是,小車會跑出限定範圍。

對此,作者給出解釋,在權重趨於0的情況下,網路的輸出也會趨於0,所以後期的優化很難達到較好的性能。
傳送門
源代碼:
https://github.com/weightagnostic/weightagnostic.github.io
本文轉載於公眾號 人工智慧學家,原文地址



Comments