在之前的文章中，無監督學習是作為一組統計工具引入的，其中有一組特徵，但沒有目標。因此，本教程將與其他教程不同，因為我們無法進行預測。

相反，我們將使用k-means聚類來對圖像執行顏色量化。

然後，我們將使用PCA來減少維度和數據集的可視化。

完整的筆記本電腦，請點擊這裡。

旋轉你的Jupyter筆記本，讓我們走吧！

建立

在開始任何實現之前，我們將導入一些稍後將變得方便的庫：

與以前的教程不同，我們不會導入數據集。相反，我們將使用scikit-learn庫提供的數據。

顏色量化 – k均值聚類

很快，顏色量化是減少圖像中使用的不同顏色數量的技術。這對於壓縮圖像同時保持圖像的完整性特別有用。

首先，我們導入以下庫：

請注意，我們導入了一個名為load_sample_image的示例數據集。這隻包含兩個圖像。我們將使用其中一個來執行顏色量化。

所以，讓我們展示一下我們將用於此練習的圖像：

你應該看到：

原始圖像

現在，對於顏色量化，必須遵循不同的步驟。

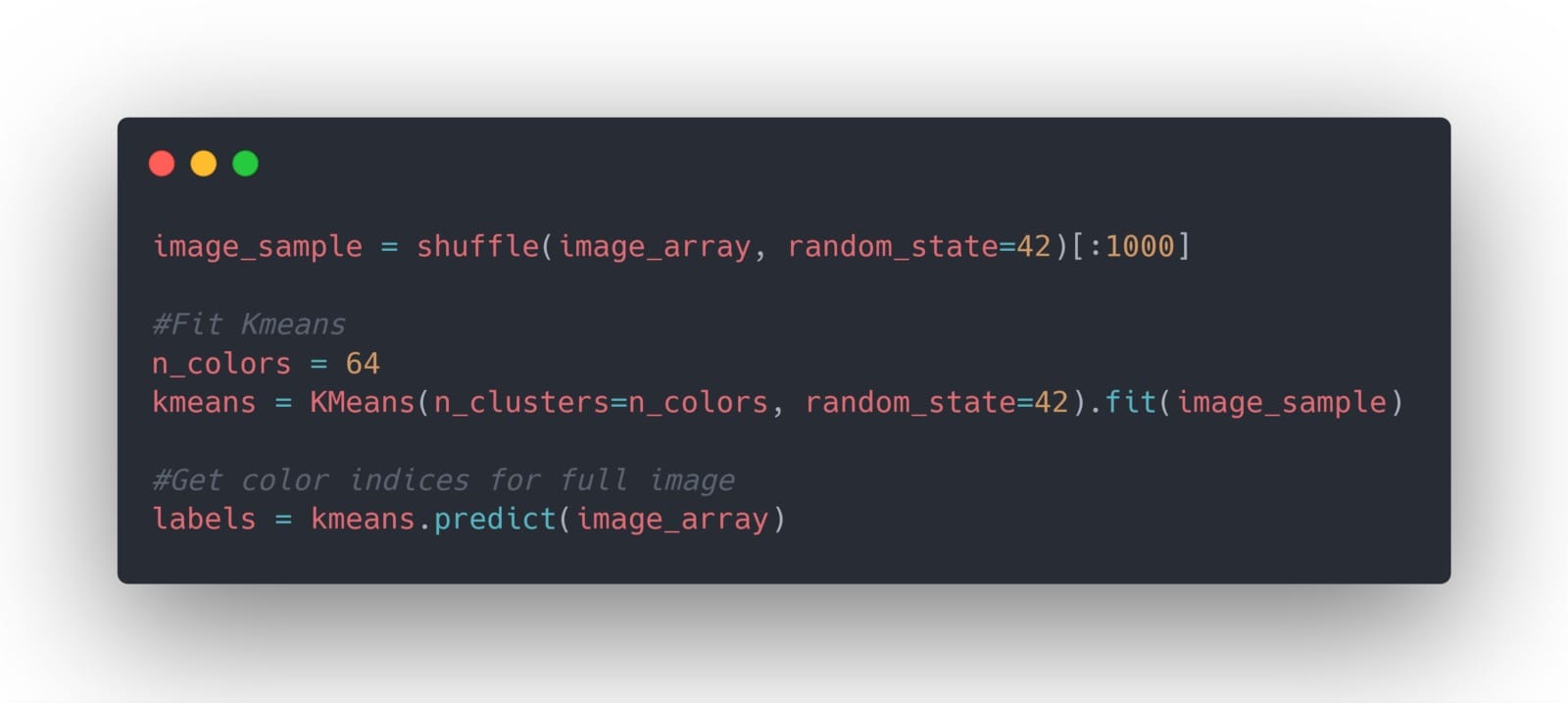
首先，我們需要將圖像更改為2D矩陣以進行操作：

然後，我們訓練我們的模型聚合顏色，以便在圖像中有64種不同的顏色：

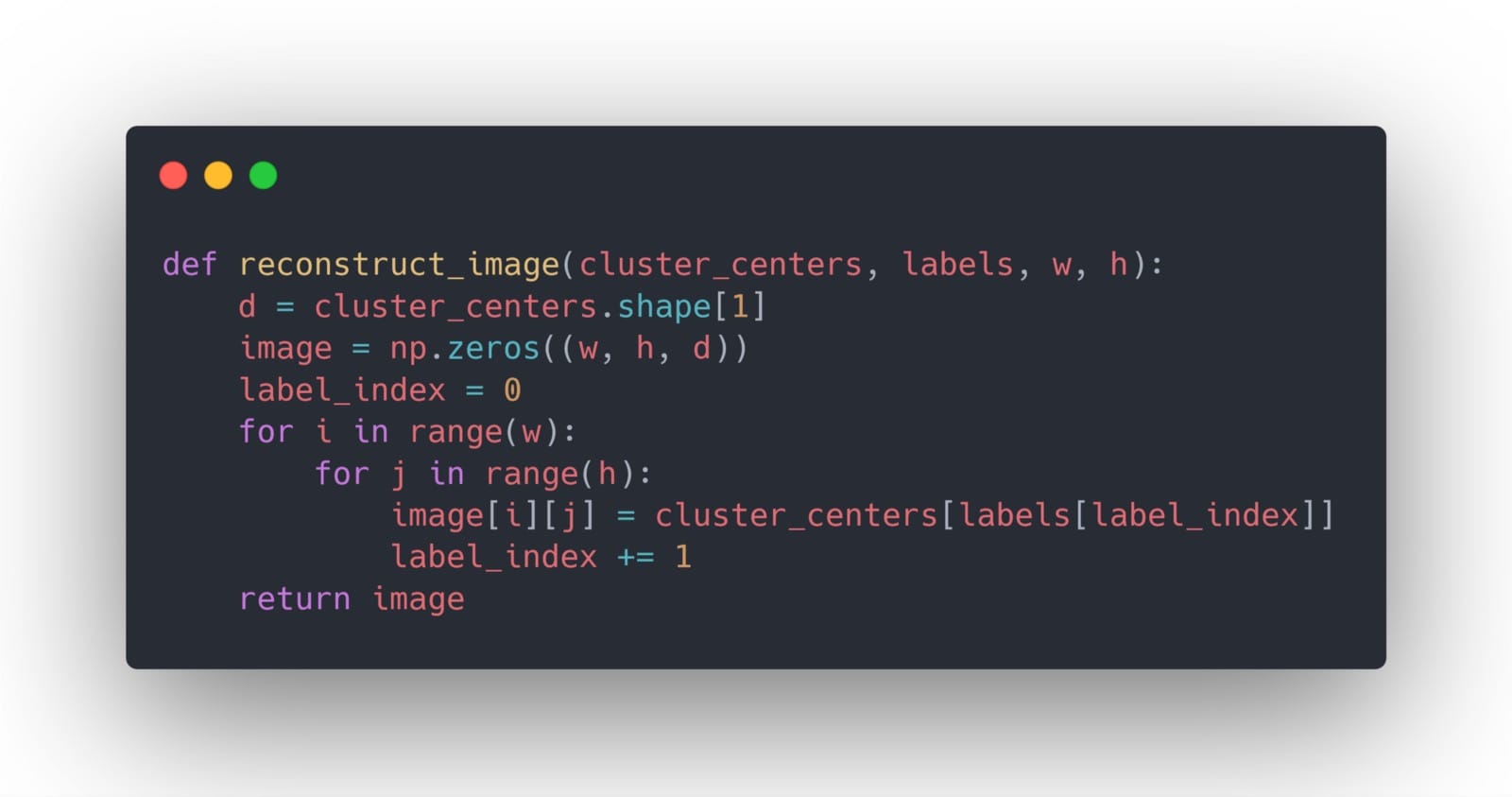
然後，我們構建一個輔助函數來幫助我們使用指定顏色的數量重建圖像：

最後，我們現在可以使用64種顏色可視化圖像的外觀，以及它與原始圖像的比較方式：

96 615色的原始圖像
64色重建圖像

當然，我們可以看到一些差異，但總體而言，圖像的完整性得到了保護！探索不同數量的集群！例如，如果指定10種顏色，可以使用以下內容：

10種顏色的重建圖像

維度降低 – PCA

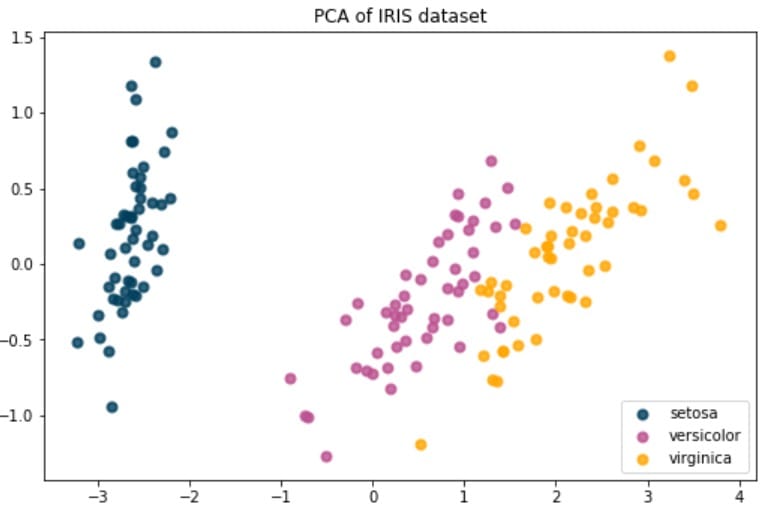
在本練習中，我們將使用PCA來減少數據集的維度，以便我們可以輕鬆地將其可視化。

因此，讓我們從scikit-learn導入虹膜數據集：

現在，我們將計算前兩個主要組件，並查看每個組件可以解釋的方差比例：

從上面的代碼塊中，您應該看到第一個主成分包含92％的方差，而第二個主成分包含5％的方差。因此，這意味著只有兩個特徵足以解釋數據集中97％的方差！

現在，我們可以使用它來輕鬆地在兩個維度上繪製數據：

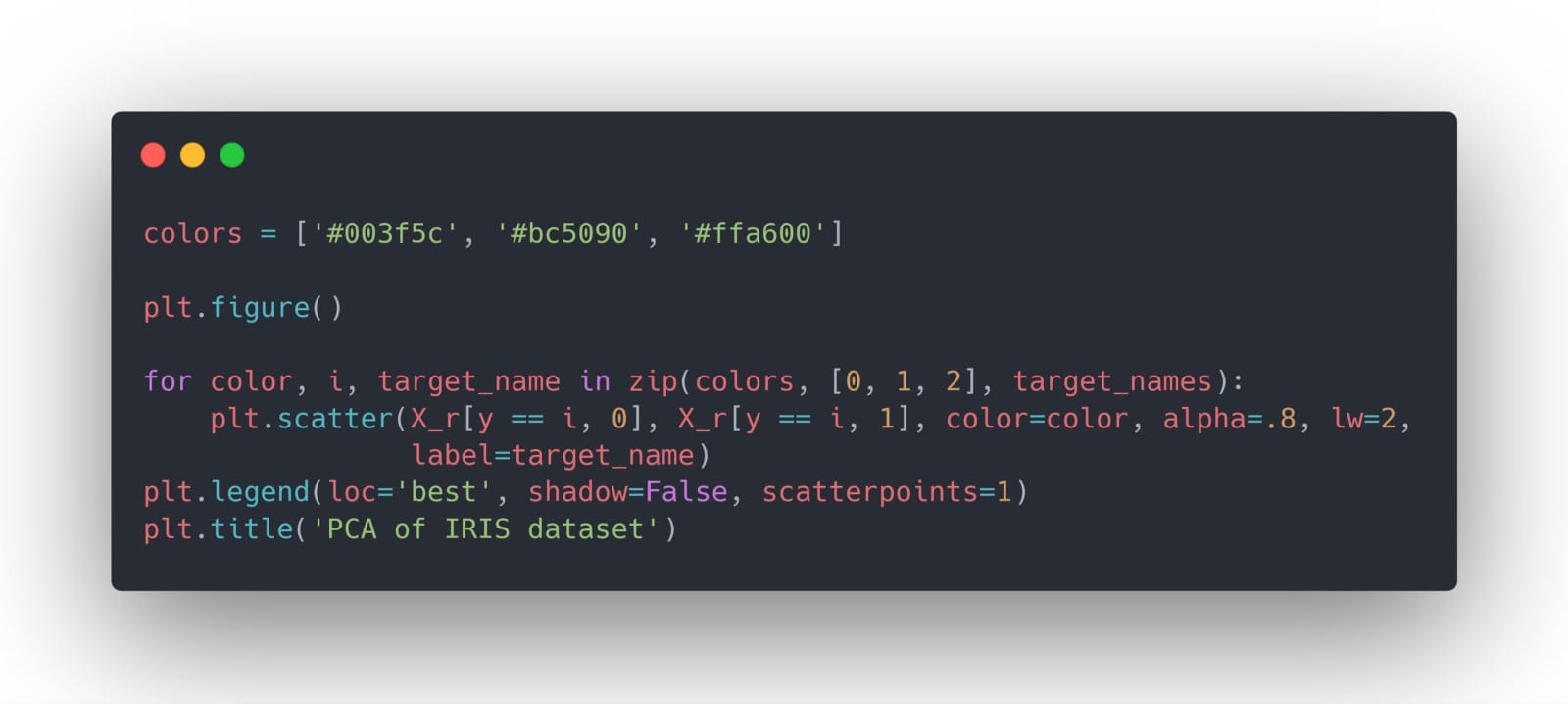
你得到：

而已！您現在知道如何實現k-means和PCA！同樣，請記住，無監督學習很難，因為沒有誤差指標來評估演算法的執行情況。而且，這些技術通常在進行監督學習之前用於探索性數據分析。

本文轉自towardsdatascience，原文地址