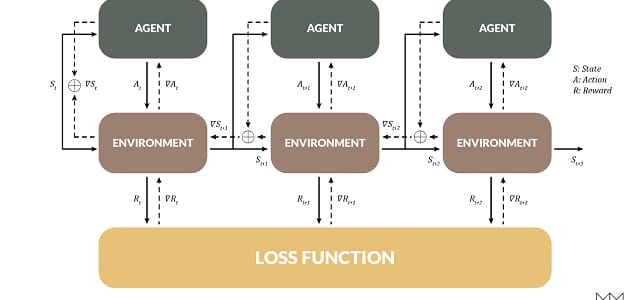
我們討論了可區分編程的概念,我們將現有程序整合到深度學習模型中。但是,如果你是一名研究人員,比如一輛自動駕駛汽車,那麼可區分編程在實踐中意味着什麼呢?它如何影響我們表達問題的方式,訓練我們的模型,策劃我們的數據集,以及最終我們實現的結果?
本文展示了DP可以為一些簡單但經典的控制問題帶來什麼,我們通常會使用強化學習(RL)。基於DP的模型不僅學習了比RL更有效的控制策略,而且還能更快地訓練數量級。該代碼是所有可用來為自己運行的-他們會在幾秒鐘內大部分列車上的任何筆記本電腦。
跟隨漸變
差異化是深度學習的關鍵; 給定函數y = f(x)y = f(x)我們使用gradient \ frac {dy} {dx} dxdy來計算xx的變化將如何影響yy。儘管有數學服裝,但漸變實際上是一個非常通用和直觀的概念。忘掉你在學校必須盯着的公式; 讓我們做一些更有趣的事情,比如扔東西。

當我們用投石機扔東西時,我們的xx代表一個設置(比如,配重的大小,或釋放角度),而yy是射彈在着陸前行進的距離。如果你想瞄準,漸變會告訴你一些非常有用的東西 – 目標的改變是增加還是減少距離。要最大化距離,只需按照漸變。
好吧,但我們怎麼能得到這個神奇的數字呢?訣竅是一個稱為算法區分的過程,它不僅可以區分你在學校學到的簡單公式,還可以區分任何複雜程序 – 比如我們的投石機模擬器。結果是我們可以採用一個簡單的模擬器,用Julia和DiffEq編寫,沒有深入學習,並在單個函數調用中獲得漸變。
# what you did in school
gradient(x -> 3x^2 + 2x + 1, 5) # (32,)
# something a little more advanced
gradient((wind, angle, weight) -> Trebuchet.shoot(wind, angle, weight),
-2, 45, 200) # (4.02, -0.99, 0.051)現在我們有了它,讓我們用它做一些有趣的事情。
扔東西
使用它的一種簡單方法是將投石機對準目標,使用漸變來微調釋放角度; 這種事情在參數估計的名義下很常見,我們之前已經介紹了類似的例子。我們可以通過meta來使事情變得更有趣:不是在給定單個目標的情況下瞄準投石機,我們將優化可以針對任何目標瞄準它的神經網絡。以下是它的工作原理:神經網絡有兩個輸入,目標距離(米)和當前風速。網絡吐出投入設置的投石機設置(配重的質量和釋放角度),模擬器計算實現的距離。然後我們與目標進行比較,並在整個鏈中反向傳播,端到端,調整網絡的權重。我們的“數據集”是一組隨機選擇的目標和風速。
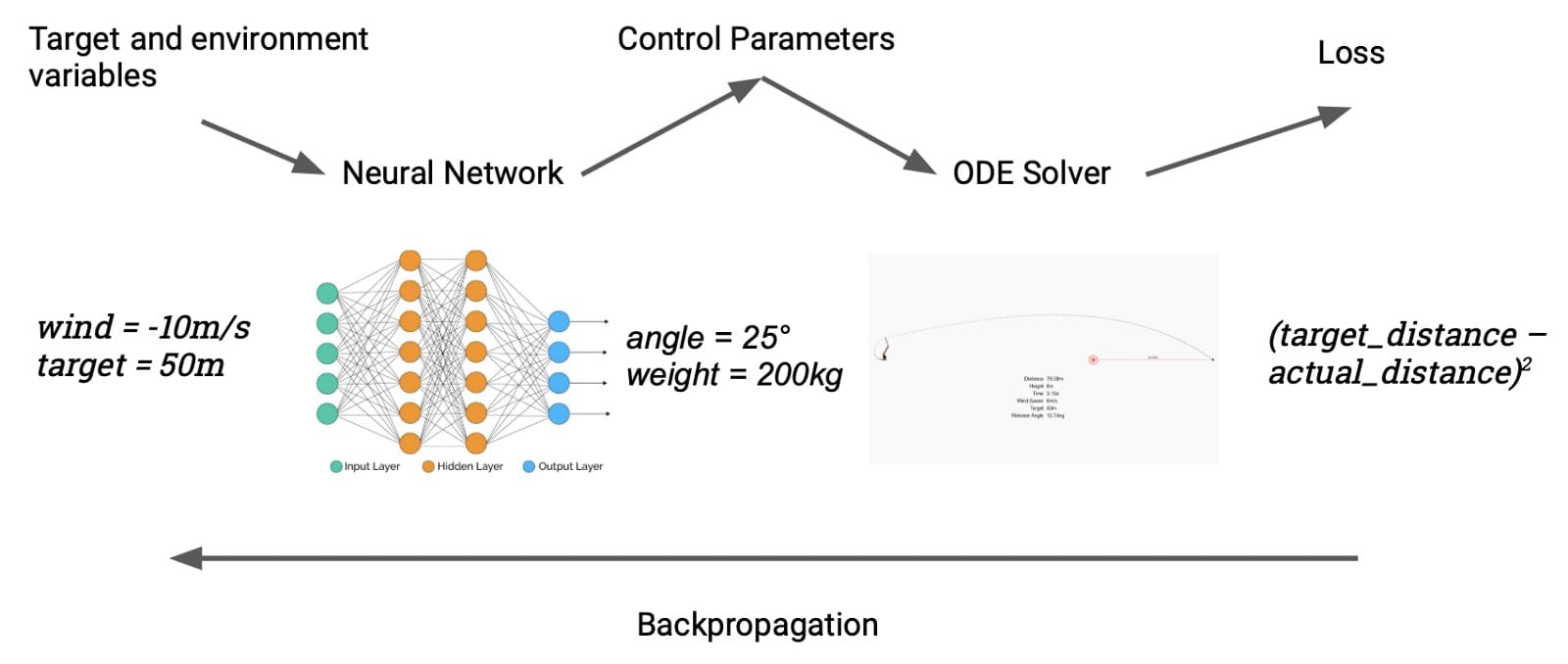
這個簡單模型的一個很好的特性就是訓練它很快,因為我們已經完全以可微分的方式表達了我們對模型的要求。最初,它看起來像這樣:

經過大約五分鐘的培訓(在我的筆記本電腦CPU的單核上),它看起來像這樣:

如果你想嘗試推動它,請調高風速:

它只有16厘米,或約0.3%。
這是關於最簡單的控制問題,我們主要用於說明目的。但是,我們可以以更高級的方式將相同的技術應用於經典的RL問題。
購物車,遇見波蘭人
一個更容易識別的控制問題是CartPole,這是強化學習的“你好世界”。任務是通過向左或向右推動其基座來學習平衡直立桿。我們的設置大致類似於投石機案:Julia實施意味着我們可以直接將環境產生的獎勵視為損失。DP允許我們從無模型轉換為基於模型的RL無縫切換。
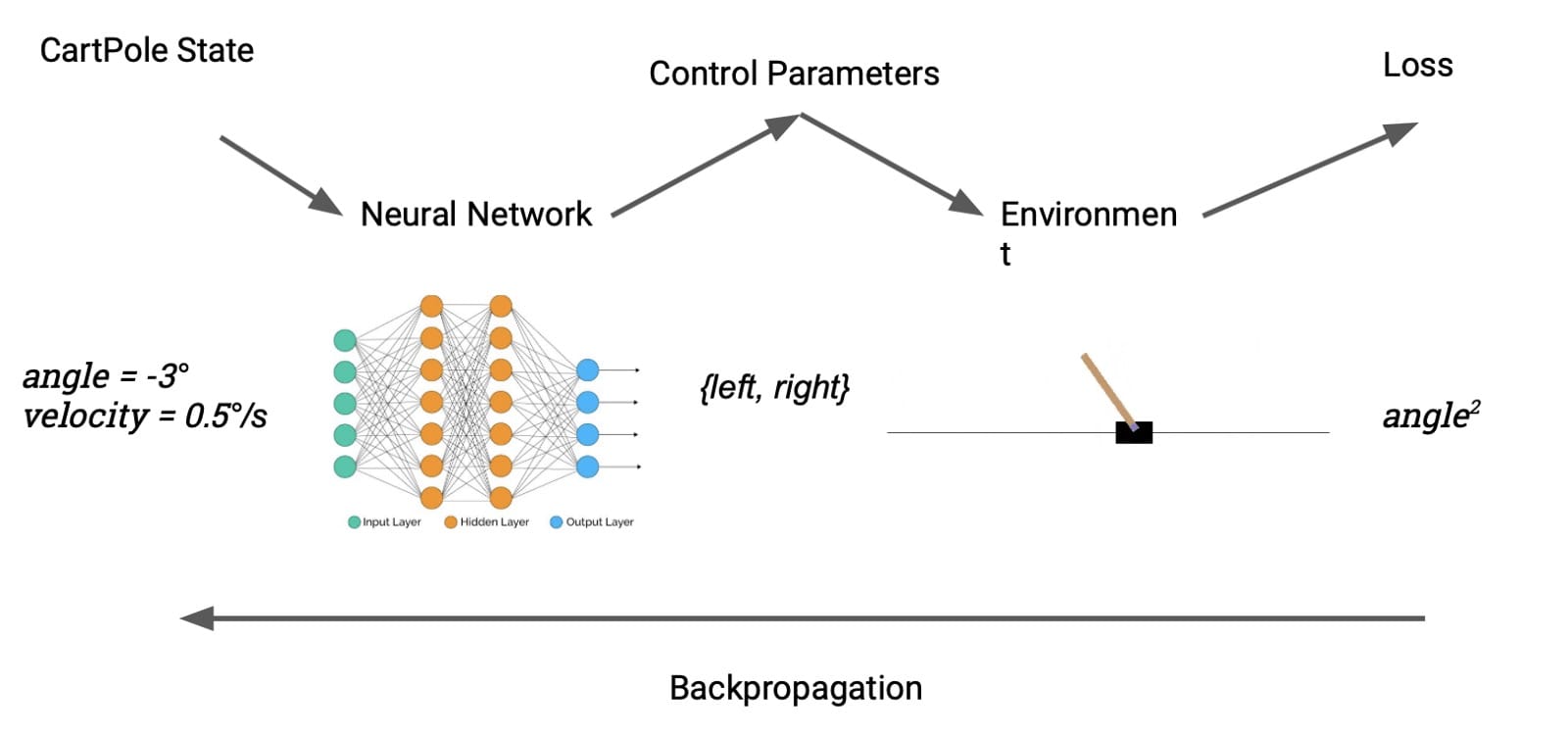
精明的讀者可能會注意到一個障礙。cartpole的動作空間 – 向左或向右輕推 – 是離散的,因此不可區分。我們通過引入可區分的離散化來解決這個問題,定義如下:
\ begin {aligned} f(x)&amp; = \ begin {cases} 1&amp; x \ ge 0 \\ -1&amp; x&lt; 0 \ end {cases} \\ \ frac {df} {dx}&amp; = 1 \ end {aligned} f(x)dxdf = {1-1x≥0x<0 = 1
換句話說,我們強制漸變表現得好像ff是身份函數。鑒於可分性的數學概念已經在ML中濫用了多少,我們可以在這裡作弊也許並不奇怪; 對於訓練我們需要的是一個信號來通知參數空間的偽隨機遊走,其餘的是細節。
結果不言自明。在解決問題之前,RL方法需要訓練數百集,DP模型只需要大約5集才能最終獲勝。

通過時間的鐘擺和Backprop
RL的一個重要目標是處理延遲獎勵,當一個行動在將來的幾個步驟之前幫助我們時。DP也允許這樣做,並且以一種非常熟悉的方式:當環境可以區分時,我們實際上可以使用反向傳播來訓練代理,就像一個經常性的網絡!在這種情況下,環境狀態變為在時間步長之間變化的“隱藏狀態”。
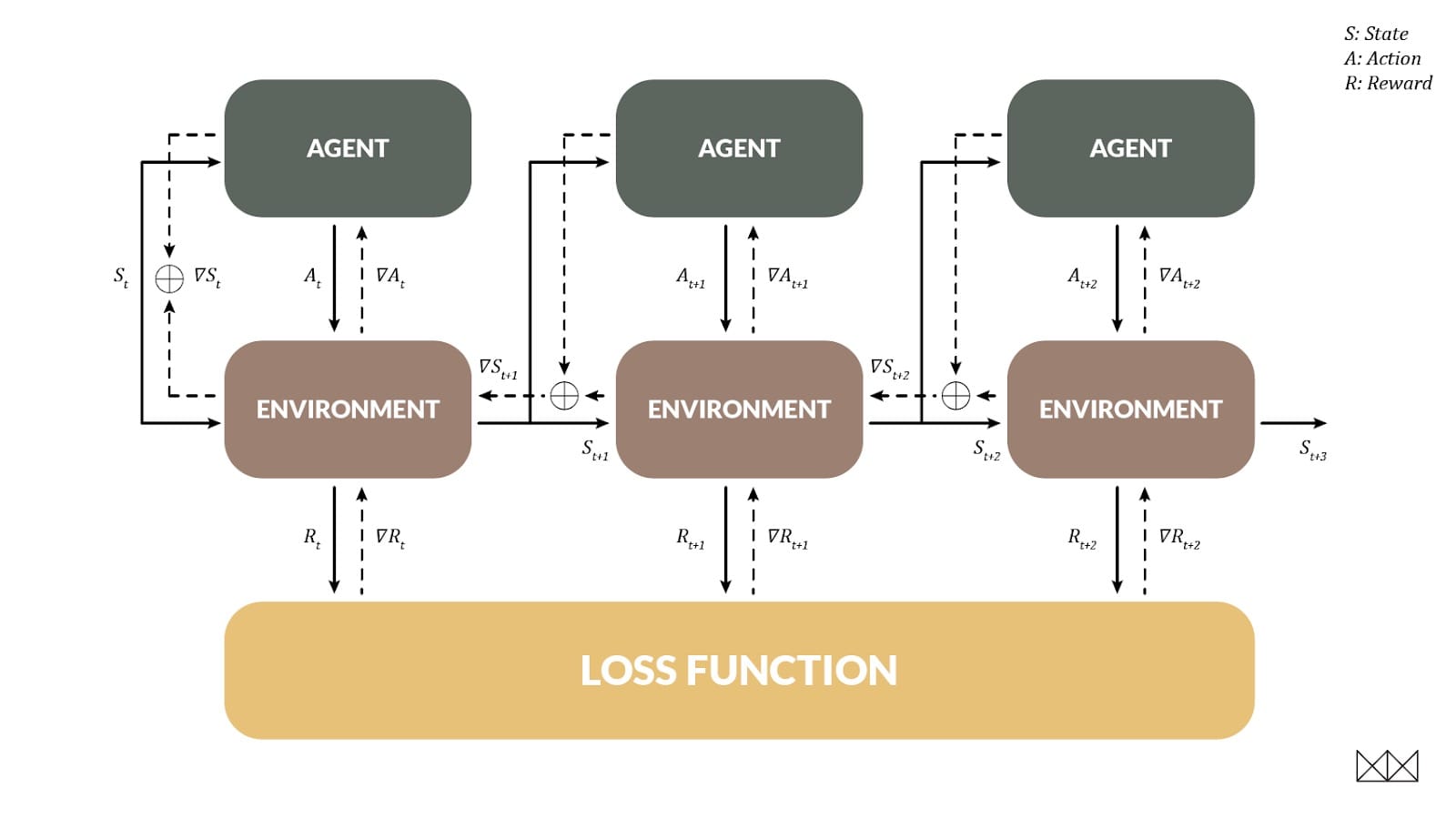
為了展示這種技術,我們研究了擺錘環境,其任務是擺錘直到它直立,以最小的努力保持平衡。這對RL型號來說很難; 在大約20次訓練之後,問題得以解決,但通常解決方案的路徑明顯不是最佳的。相比之下,BPTT可以在一集訓練中擊敗RL排行榜。實際觀看這一集展開是有益的; 在記錄開始時,策略是隨機的,並且模型隨着時間的推移而改進。學習的速度幾乎令人擔憂。

儘管只是經歷了一集,但該模型很好地處理了任何初始角度,並且具有非常接近最優策略的東西。重新啟動時,模型看起來更像這樣。

這僅僅是個開始; 我們將獲得真正的勝利,將DP應用於對RL來說太難以使用的環境。
地圖不是領土
這些玩具模型的局限在於它們將模擬的訓練環境與測試環境等同起來; 當然,現實世界並不是可以區分的。在一個更現實的模型中,模擬為我們提供了一個粗略的行為概述,並用數據進行了細化。該數據通知(比如說)風的模擬效果,進而改善模擬器傳遞給控制器的梯度質量。模型甚至可以構成控制器前向傳遞的一部分,使其能夠優化其預測,而無需從頭開始學習系統動態。探索這些新架構將有助於激發未來的工作。
結尾
核心思想是可區分編程,我們只需編寫任意數字程序並通過漸變進行優化,這是一種提供更好的深度學習模型和體系結構的強大方法 – 特別是當我們擁有一個可識別的大型代碼庫時手。所描述的玩具模型實際上只是預覽,但我們希望他們能夠直觀地了解如何以更現實的方式應用這些想法。
正如函數式編程涉及使用函數模式推理和表達算法一樣,可微分編程涉及使用可微分模式表達算法。許多這樣的設計模式已經由深度學習社區開發,例如用於處理控制問題或序列和ttree結構化數據。這篇文章介紹了幾個新的,隨着領域的成熟,將會發明更多。由此產生的程序可能會使最先進的當前深度學習架構看起來相形見絀。
本文轉自medium,原文地址



Comments