循环神经网络产生动机
假设我们现在使用传统的语言模型来做一个简单的预测任务,存在这样一个句子:
读芯术是一个优秀的公众号,里面有着很多有用的信息,我经常在___中寻找信息、获取知识。
如果我们采用n-gram模型去预测空格的内容,比如2-gram,模型会给出“在”之后出现概率最高的词。虽然在我们看来,“读芯术”是高概率的选项,但在训练了很多资料后,“读芯术”出现在“在”的后面概率必然是极低的,因为我们一般会说“在家”等常用词。当然,我们可以将模型看到的范围继续扩大,直到在前文中看到读芯术这个名称,但是这样的思路在实践中并不可行,N越大,马尔可夫链就越长,数据稀疏严重,计算困难,更重要的是,我们需要将这个N设定为一个固定的值,这样就无法处理任意长度的句子。
带有循环结构的网络都可以被叫做循环神经网络(recurrent neural network),RNN可以非常有效的解决这个问题,从简单的理论上来说,它可以处理任意长度的序列,并且不需要提前将N固定住,灵活性更高。
卷积神经网络也可以处理时间序列的问题,尤其是在我们关心某些特征是否出现,而不是它具体位置的时候,CNN具有一定的优势。但在处理自然语言类型的数据时,比如在情感分类问题中,我们将文本分成正面和负面,CNN在可能会处理成某些词语的出现就意味着正面情感,比如“喜欢”,“美”,如果这样一个句子:
我不是不喜欢这部电影,这部电影不能说不美,但是……
我们能很快的知道,这个评价是一个负面评价。那么如果只提取特征,而忽略了词与词之间的关系,CNN可能会发现文本存在“喜欢”就将其归为正面,看到“不喜欢”就归为负面,再看到“不是不喜欢”就又将其归为正面,显然是不合理的。这时就需要我们采用语言模型来理解这句话的意思。
理解循环神经网络
我们经常会在学习资料中见到RNN的图示:

这幅图对于初学者来说是不友好的,而且非常容易产生更多的误解,虽然我们能从中看到时间序列的依赖性,从st-1到st中添加了传播的箭头,表示有信息从前面的神经元直接流向后面的神经元,但关于更多问题是这张图无法告诉我们的,比如:
- 数据是同时进入的吗?
- 在最开始的时候,第一个单元是否也会接受前一个神经元的输入?如果是,第一个神经元没有前一个神经元,那么这个输入来源于哪里?
- 在同一层的隐藏单元中进行传播的权值矩阵W,以及输入到隐层的权值矩阵U,隐层到输出的权值矩阵V,为什么是相同的?
虽然上图是一个使用广泛的示意图,事实上,更好理解循环结构的方式并非如此。
为了更好的帮助大家理解循环结构,我画了几幅草图。设想一个简单的前馈神经网络,输入、输出、隐层均只有一个神经元,如下图。这里的圆圈没有任何抽象的含义,一个圆圈就是一个神经元:
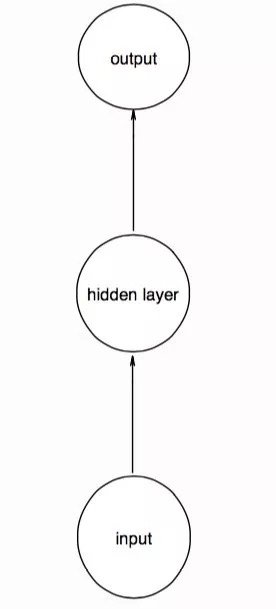
当我们输入时间序列的第一个数据点后,就把这时隐层的值用一个记忆单元存起来,这个记忆单元并不是一个实体,而是一个用来存取东西的结构:
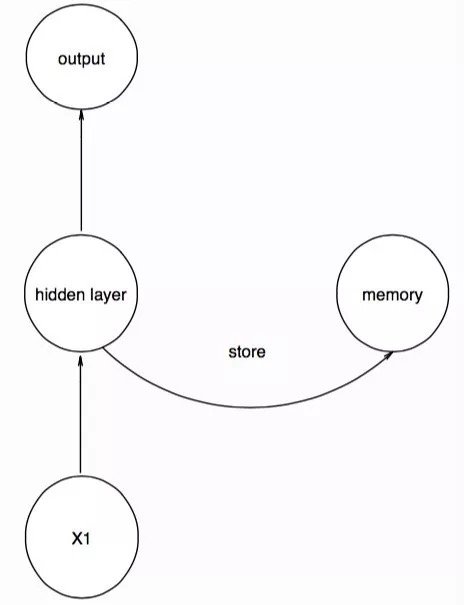
我们存入的memory单元的作用就存取了X1的特征,当我们输入时间序列的第二个数据点时,要注意,网络的结构保持不变,只是我们将memory中的信息也输入到隐层中,相当于,第二个数据点的隐层接受了数据和第一个数据点的特征进行输出,同时将此时隐层的信息返回到memory,再次存起来:
在第三个数据点输入的时候,memory单元所操作就是前一步得到的信息,并将得到的信息存起来,供下一个时间步的输入:

这样依次进行下去,我们就得到了与大家喜闻乐见的那幅图类似的结构,为了表达先前的信息对现在的影响,我们在输入memory单元时,采用一个权值矩阵W参数化记忆单元,那么一一对应关系就变成了:
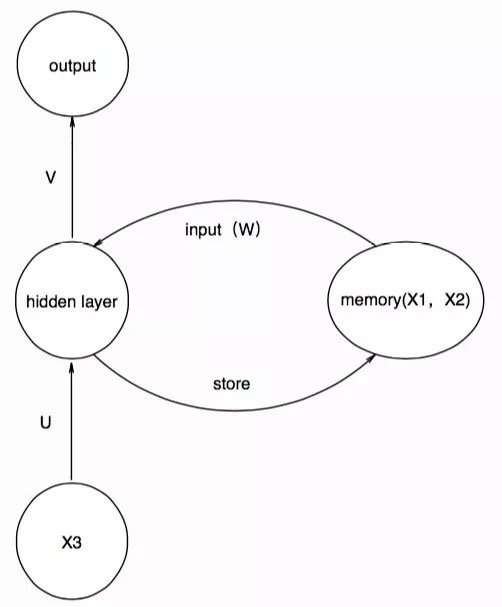
在这里,我们将每个圆圈都理解为一个神经元,但如果我们将一个圆圈理解为一层神经元,也就是将其抽象成结构,输入,隐层,输出都是多维的,并将其按照时间展开,就会得到:
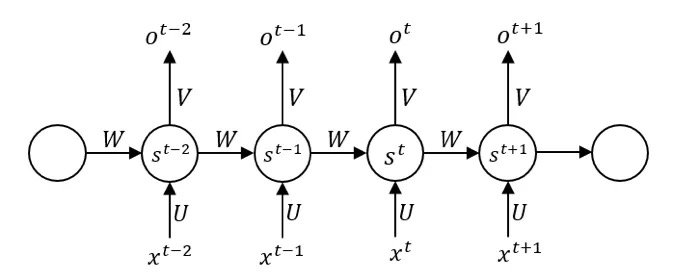
在此基础上,我们解释上述的问题:
- 数据是同时进入的吗?显然不是,数据是按照顺序进入,我们在处理序列化的数据时,往往会在用滑动窗口的办法来调整不同的结构。
- 在最开始的时候,第一个单元是否也会接受前一个神经元的输入?如果是,但第一个神经元没有前一个神经元,那么这个输入来源于哪里?
我们在第一个数据点进入时,需要对memory单元设置初始值,这个初始值可以作为一个参数,也可以将其简单的设置为零,表示前面没有任何信息。 - 在同一层的隐藏单元中进行传播的权值矩阵W,以及输入到隐层的权值矩阵U,隐层到输出的权值矩阵V,为什么是相同的?
这是一个非常重要的问题,也是我们无法从图中推断的知识。大大减少参数数量是一个原因,但不是本质上的。我们先不考虑矩阵W,只考虑普通的神经网络,因为在序列上不同数据,都是采用相同的神经网络。CNN用参数共享的卷积核来提取相同的特征,在RNN中,使用参数共享的U,V来确保相同的输入产生的输出是一样,比如一段文本中,可能会出现大量的“小狗”,参数共享使得神经网络在输入“小狗”的时候,产生一样的隐层和输出。
此时,我们讨论矩阵W,参数共享的矩阵W确保了对于相同的上文,产生相同的下文。




Comments