目前,我们在构建和优化机器学习模型方面已经做了大量的工作,但是在所有这些艰苦工作之后,我们不免生出这样一个疑问:如何比较我们已经构建的模型呢? 若要在模型A和模型B之间做比较,哪个是赢家,为什么? 又或者,能否将两个模型组合起来以实现性能的最优化?
一个非常肤浅的方法是比较测试集的总精确度,例如,模型A的精确度是94%,而模型B的精确度是95%,然后轻率地得出结论:模型B更胜一筹。事实上,若对两模型进行比较,需要考虑的方面很多,绝不仅仅是总精确度。
本文将用浅显易懂的语言来解释统计学,所以这篇文章对于那些不是很擅长统计数据,但是想多学一点的人来说是一个很好的读物。
1. “了解”数据
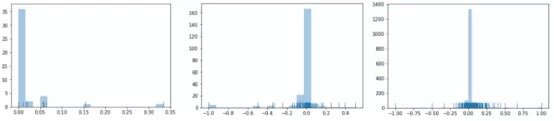
若可能的话,想出一些能反映实际情况的图是个好主意。要绘出这方面的图虽奇怪,但却能为我们提供一些数字所不能提供的见解。
在一个项目中,基于同一测试集,对两个机器学习模型在预测用户对其文档所承担的税额的准确性方面进行比较。一般认为,通过用户id进行数据整合,并计算每个模型能够准确预测税额的比例是一种好办法。
假设数据集很大,故将数据解析分解成不同区域,并将重点放在较小的数据子集上,每个子集的准确性可能有所不同。在处理异常庞大的数据集时,通常采取上述方法,因为一次性处理大量的数据是不现实的,更不用说得出可靠的结论(稍后会讨论关于样本大小的问题)。大数据集的巨大优势之一在于,不仅可获得大量的可用信息,而且可放大数据并对某个像素子集上的情况进行研究。
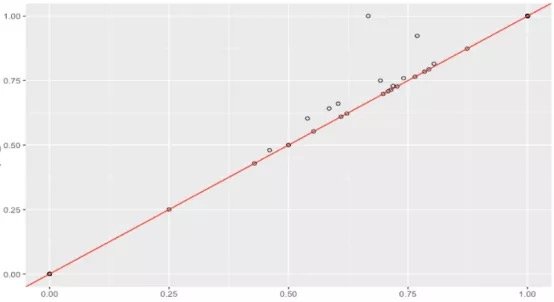
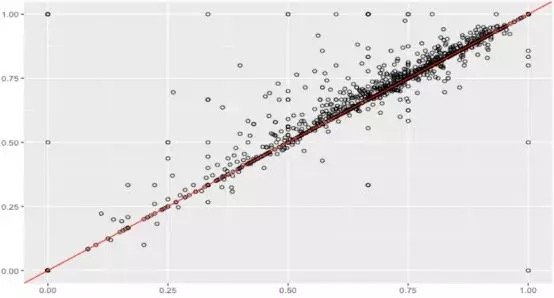
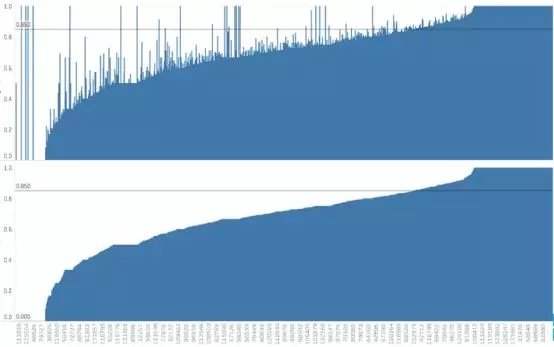
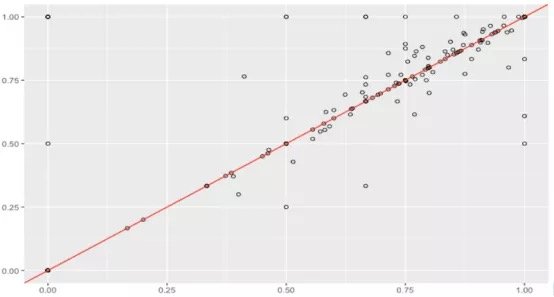
据此,我们有理由怀疑其中一个模型在某些子集上的表现很出色,但在其他子集上的表现却相当一致。这是我们从仅仅比较模型的总精准度向前迈出的一大步。但这种怀疑可通过假设检验作进一步调查。假设检验比人眼能更好地发现差异——我们在测试集中拥有的数据有限,若比较不同测试集上的模型,我们可能会好奇其准确性将如何改变。遗憾的是,我们并不总是能够想出一个不同的测试集,因此,了解目前已有的一些统计数据可能有助于对模型准确性的研究。
2. 假设检验:现在就开始!
这乍一看似乎微不足道,你可能以前见过:
1. 建立H0和H1
2. 给出一个检验统计量,假设其为正态分布
3. 计算p值
4. 若p < = 0.05则排除H0,那么就完成了!
在实践中,假设检验比较复杂和棘手。然而,人们在假设检验中却总是不太谨慎,以致于曲解结果。让我们一步一步来:
步骤1: 建立H0: 原假设/零假设为,即两个模型之间没有统计学上的显著差异;H1:备择假设/对立假设,即两个模型在其准确性上存在统计学上的显著差异。 由你来确定模型A ! = B (双侧检验) 或模型A < 模型B或模型A>模型B(单侧检验)
步骤2:提出一种检验统计量,可在观测数据中对将零假设从备择假设中区分开来的行为进行量化处理。这有多种选择,即使是最好的统计学家也可能对数量未知的统计检验毫无头绪,别担心! 因为要考虑很多假设和事实,所以一旦数据已知,就可以从中选择合适的方法。关键是要理解假设检验是如何工作的,而实际的检验统计量只是一种利用软件简化计算的工具。
切记,在进行任何统计检验之前,还需要满足诸多假设。你可以查找每一个检验所需的假设; 然而,现实生活中的绝大多数数据并不能完全满足所有条件,所以你可以适当放宽条件! 但如果数据严重偏离正态分布该怎么办呢?
统计检验有两大类: 参数检验和非参数检验。简言之,这两类统计检验之间的主要区别是,参数检验需要对总体分布作出一些假设,而非参数检验则更稳健一些 (请不要使用参数)。
在上面那个项目的分析中,如果你想采用配对样本t检验(https://www.statisticssolutions.com/manova-analysis-paired-sample-t-test/),但由于数据不是正态分布的,所以可以选择威氏符号秩次检验(https://www.statisticssolutions.com/how-to-conduct-the-wilcox-sign-test/)(配对样本的非参数检验)。你可以自行决定在分析中使用哪种检验统计量,但一定要确保满足假设。
步骤3: 确定p值。p值的概念有点抽象: p值只是一个用来衡量否定原假设的理由的数字,若否定原假设的理由越充分,p值就越小。若p值足够小,我们就有充分的理由来否定原假设。
幸运的是,p值在Python的R中很容易找到,所以无需自己动手。可以选择在R中进行假设检验,因为其有更多可用选项。以下是一段代码。可以看到在子集2上,我们得到了一个小的p值,但是该置信区间是无用的。
> wilcox.test(data1, data2, conf.int = TRUE, alternative=”greater”, paired=TRUE, conf.level = .95, exact = FALSE)
V = 1061.5, p-value = 0.008576
alternative hypothesis: true location shift is less than 0
95 percent confidence interval:
-Inf -0.008297017
sample estimates:
(pseudo)median
-0.02717335
步骤4:该步骤很简单,如果p值小于给定的alpha(通常为0.05),则有理由否定原假设,接受备择假设。否则,就没有充分的理由否定原假设, 但这并不意味着原假设正确。事实上,原假设可能仍然是错误的,只是没有充足的数据作为拒否定该假设的证据。若alpha的值为0.05=5%,这意味着得出存在差异这一错误结论的风险只有5% (即第一类错误)。
你可能会问自己:为什么我们不能将alapha的值取为1%而是5%呢?因为那会使分析更加保守,将增加否定原假设的难度(而我们的目标是否定原假设)。
最常用的alpha值是5%,10%和1%,不过你可以选择任何你想要的alpha值。这取决于你愿意承担多大的风险。
alpha值能为0%吗?即不存在犯第一类错误的可能性。这是不可能的,事实上,你总会犯错误,所以选择0%是没有意义的。我们需要给自己的小差错留点余地。
若想避免“p值被篡改”(p-hack),可增加alpha值,否定原假设,但需降低置信度(随着alpha值的增加,置信度下降,两者只能取其一)。
3. 因果分析:统计学意义 vs. 现实意义
若所得p值非常小,那当然意味着这两个模型的准确性在统计学上有显著的差异。之前的例子中,我们确实得到了一个很小的p值,所以从数学上来说,模型当然是不同的,但是“有意义”并不意味着“重要”。这种差异真的有什么意义吗? 这种微小的差异与业务问题相关吗?
统计学意义是指样本中所观测到的均值差异不可能是由于抽样误差造成的。给定一个足够大的样本,尽管总体差异看起来并不显著,但我们仍然可以发现其统计学意义。另一方面,现实意义则着眼于差异是否大到足以具有现实价值。统计学意义是严格定义的,而现实意义则更加直观、主观。

在这一点上,你可能已经意识到p值并不像你所想的那样强大。我们还需要进行更多调查,同时也要考虑效应大小(effect size)。效应大小衡量的是差异的大小,若存在统计学上显著的差异,我们可能会对其大小感兴趣。效应大小强调的是差异的大小,而不是样本大小,切记不要将两者混淆。
> abs(qnorm(p-value))/sqrt(n)
0.14
# the effect size is small
什么是低效应、中等效应、高效应? 传统的临界值分别是0.1、0.3和0.5,但这实际上取决于你的业务问题。
样本容量又是什么情况呢? 如果样本数太小,结果就不可靠了,不过这无关紧要。那如果样本量太大怎么办? 这似乎很不错——但是在这种情况下,即使是非常小的差异也可以通过假设检验检测出来。在数据这么多的情形下,即使是微小的偏差也可被认为是显著的。这就是效应量的有用之处。
还有更多的事情要做,我们还可以尝试确定检验以及最优样本容量。不过现在用不着。
若假设检验很成功,其在模型比较中会非常有用。一般步骤包括建立原假设(H0)和备择假设(H1),对统计数据进行计算并找到p值,但是解释结果还需要直觉、创造力和对业务问题的更加深入理解。
请记住,如果检验是基于一个非常大的测试集,那么所发现的具有统计学意义的关系可能没有太多现实意义。不要盲目相信那些神奇的p值: 放大数据并进行因果分析是个不错的方法。



Comments