目前,我們在構建和優化機器學習模型方面已經做了大量的工作,但是在所有這些艱苦工作之後,我們不免生出這樣一個疑問:如何比較我們已經構建的模型呢? 若要在模型A和模型B之間做比較,哪個是贏家,為什麼? 又或者,能否將兩個模型組合起來以實現性能的最優化?
一個非常膚淺的方法是比較測試集的總精確度,例如,模型A的精確度是94%,而模型B的精確度是95%,然後輕率地得出結論:模型B更勝一籌。事實上,若對兩模型進行比較,需要考慮的方面很多,絕不僅僅是總精確度。
本文將用淺顯易懂的語言來解釋統計學,所以這篇文章對於那些不是很擅長統計數據,但是想多學一點的人來說是一個很好的讀物。
1. 「了解」數據
若可能的話,想出一些能反映實際情況的圖是個好主意。要繪出這方面的圖雖奇怪,但卻能為我們提供一些數字所不能提供的見解。
在一個項目中,基於同一測試集,對兩個機器學習模型在預測用戶對其文檔所承擔的稅額的準確性方面進行比較。一般認為,通過用戶id進行數據整合,並計算每個模型能夠準確預測稅額的比例是一種好辦法。
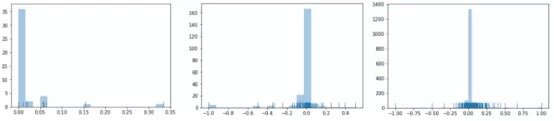
假設數據集很大,故將數據解析分解成不同區域,並將重點放在較小的數據子集上,每個子集的準確性可能有所不同。在處理異常龐大的數據集時,通常採取上述方法,因為一次性處理大量的數據是不現實的,更不用說得出可靠的結論(稍後會討論關於樣本大小的問題)。大數據集的巨大優勢之一在於,不僅可獲得大量的可用信息,而且可放大數據並對某個像素子集上的情況進行研究。
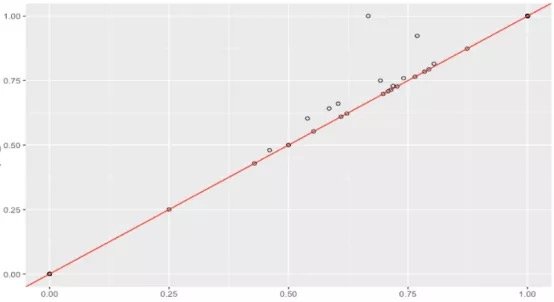
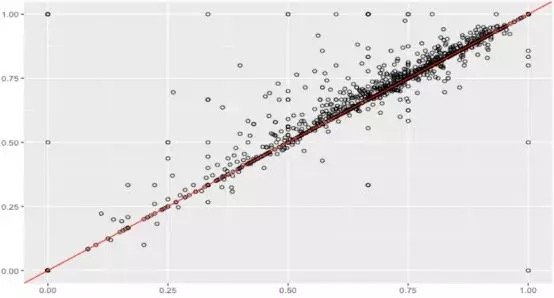
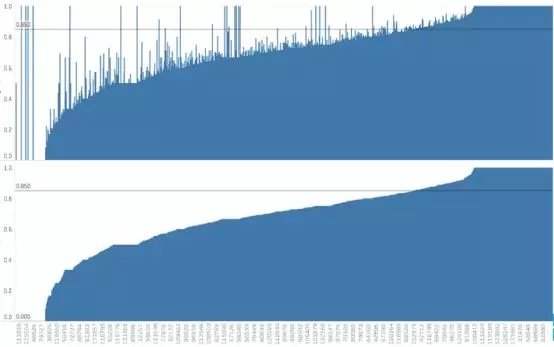
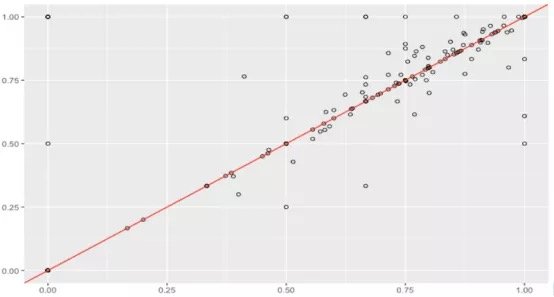
據此,我們有理由懷疑其中一個模型在某些子集上的表現很出色,但在其他子集上的表現卻相當一致。這是我們從僅僅比較模型的總精準度向前邁出的一大步。但這種懷疑可通過假設檢驗作進一步調查。假設檢驗比人眼能更好地發現差異——我們在測試集中擁有的數據有限,若比較不同測試集上的模型,我們可能會好奇其準確性將如何改變。遺憾的是,我們並不總是能夠想出一個不同的測試集,因此,了解目前已有的一些統計數據可能有助於對模型準確性的研究。
2. 假設檢驗:現在就開始!
這乍一看似乎微不足道,你可能以前見過:
1. 建立H0和H1
2. 給出一個檢驗統計量,假設其為正態分佈
3. 計算p值
4. 若p < = 0.05則排除H0,那麼就完成了!
在實踐中,假設檢驗比較複雜和棘手。然而,人們在假設檢驗中卻總是不太謹慎,以致於曲解結果。讓我們一步一步來:
步驟1: 建立H0: 原假設/零假設為,即兩個模型之間沒有統計學上的顯著差異;H1:備擇假設/對立假設,即兩個模型在其準確性上存在統計學上的顯著差異。 由你來確定模型A ! = B (雙側檢驗) 或模型A < 模型B或模型A>模型B(單側檢驗)
步驟2:提出一種檢驗統計量,可在觀測數據中對將零假設從備擇假設中區分開來的行為進行量化處理。這有多種選擇,即使是最好的統計學家也可能對數量未知的統計檢驗毫無頭緒,別擔心! 因為要考慮很多假設和事實,所以一旦數據已知,就可以從中選擇合適的方法。關鍵是要理解假設檢驗是如何工作的,而實際的檢驗統計量只是一種利用軟件簡化計算的工具。
切記,在進行任何統計檢驗之前,還需要滿足諸多假設。你可以查找每一個檢驗所需的假設; 然而,現實生活中的絕大多數數據並不能完全滿足所有條件,所以你可以適當放寬條件! 但如果數據嚴重偏離正態分佈該怎麼辦呢?
統計檢驗有兩大類: 參數檢驗和非參數檢驗。簡言之,這兩類統計檢驗之間的主要區別是,參數檢驗需要對總體分佈作出一些假設,而非參數檢驗則更穩健一些 (請不要使用參數)。
在上面那個項目的分析中,如果你想採用配對樣本t檢驗(https://www.statisticssolutions.com/manova-analysis-paired-sample-t-test/),但由於數據不是正態分佈的,所以可以選擇威氏符號秩次檢驗(https://www.statisticssolutions.com/how-to-conduct-the-wilcox-sign-test/)(配對樣本的非參數檢驗)。你可以自行決定在分析中使用哪種檢驗統計量,但一定要確保滿足假設。
步驟3: 確定p值。p值的概念有點抽象: p值只是一個用來衡量否定原假設的理由的數字,若否定原假設的理由越充分,p值就越小。若p值足夠小,我們就有充分的理由來否定原假設。
幸運的是,p值在Python的R中很容易找到,所以無需自己動手。可以選擇在R中進行假設檢驗,因為其有更多可用選項。以下是一段代碼。可以看到在子集2上,我們得到了一個小的p值,但是該置信區間是無用的。
> wilcox.test(data1, data2, conf.int = TRUE, alternative=”greater”, paired=TRUE, conf.level = .95, exact = FALSE)
V = 1061.5, p-value = 0.008576
alternative hypothesis: true location shift is less than 0
95 percent confidence interval:
-Inf -0.008297017
sample estimates:
(pseudo)median
-0.02717335
步驟4:該步驟很簡單,如果p值小於給定的alpha(通常為0.05),則有理由否定原假設,接受備擇假設。否則,就沒有充分的理由否定原假設, 但這並不意味着原假設正確。事實上,原假設可能仍然是錯誤的,只是沒有充足的數據作為拒否定該假設的證據。若alpha的值為0.05=5%,這意味着得出存在差異這一錯誤結論的風險只有5% (即第一類錯誤)。
你可能會問自己:為什麼我們不能將alapha的值取為1%而是5%呢?因為那會使分析更加保守,將增加否定原假設的難度(而我們的目標是否定原假設)。
最常用的alpha值是5%,10%和1%,不過你可以選擇任何你想要的alpha值。這取決於你願意承擔多大的風險。
alpha值能為0%嗎?即不存在犯第一類錯誤的可能性。這是不可能的,事實上,你總會犯錯誤,所以選擇0%是沒有意義的。我們需要給自己的小差錯留點餘地。
若想避免「p值被篡改」(p-hack),可增加alpha值,否定原假設,但需降低置信度(隨着alpha值的增加,置信度下降,兩者只能取其一)。
3. 因果分析:統計學意義 vs. 現實意義
若所得p值非常小,那當然意味着這兩個模型的準確性在統計學上有顯著的差異。之前的例子中,我們確實得到了一個很小的p值,所以從數學上來說,模型當然是不同的,但是「有意義」並不意味着「重要」。這種差異真的有什麼意義嗎? 這種微小的差異與業務問題相關嗎?
統計學意義是指樣本中所觀測到的均值差異不可能是由於抽樣誤差造成的。給定一個足夠大的樣本,儘管總體差異看起來並不顯著,但我們仍然可以發現其統計學意義。另一方面,現實意義則着眼於差異是否大到足以具有現實價值。統計學意義是嚴格定義的,而現實意義則更加直觀、主觀。

在這一點上,你可能已經意識到p值並不像你所想的那樣強大。我們還需要進行更多調查,同時也要考慮效應大小(effect size)。效應大小衡量的是差異的大小,若存在統計學上顯著的差異,我們可能會對其大小感興趣。效應大小強調的是差異的大小,而不是樣本大小,切記不要將兩者混淆。
> abs(qnorm(p-value))/sqrt(n)
0.14
# the effect size is small
什麼是低效應、中等效應、高效應? 傳統的臨界值分別是0.1、0.3和0.5,但這實際上取決於你的業務問題。
樣本容量又是什麼情況呢? 如果樣本數太小,結果就不可靠了,不過這無關緊要。那如果樣本量太大怎麼辦? 這似乎很不錯——但是在這種情況下,即使是非常小的差異也可以通過假設檢驗檢測出來。在數據這麼多的情形下,即使是微小的偏差也可被認為是顯著的。這就是效應量的有用之處。
還有更多的事情要做,我們還可以嘗試確定檢驗以及最優樣本容量。不過現在用不着。
若假設檢驗很成功,其在模型比較中會非常有用。一般步驟包括建立原假設(H0)和備擇假設(H1),對統計數據進行計算並找到p值,但是解釋結果還需要直覺、創造力和對業務問題的更加深入理解。
請記住,如果檢驗是基於一個非常大的測試集,那麼所發現的具有統計學意義的關係可能沒有太多現實意義。不要盲目相信那些神奇的p值: 放大數據並進行因果分析是個不錯的方法。



Comments