最近,圖神經網絡 (GNN) 在各個領域越來越受到歡迎,包括社交網絡、知識圖譜、推薦系統,甚至生命科學。
GNN 在對圖形中節點間的依賴關係進行建模方面能力強大,使得圖分析相關的研究領域取得了突破性進展。本文旨在介紹圖神經網絡的基本知識,以及兩種更高級的算法:DeepWalk 和 GraphSage。
圖 (Graph)
在討論 GNN 之前,讓我們先了解一下什麼是圖 (Graph)。在計算機科學中,圖是由兩個部件組成的一種數據結構:頂點 (vertices) 和邊 (edges)。一個圖 G 可以用它包含的頂點 V 和邊 E 的集合來描述。
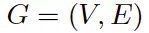
邊可以是有向的或無向的,這取決於頂點之間是否存在方向依賴關係。

頂點通常也被稱為節點 (nodes)。在本文中,這兩個術語是可以互換的。
圖神經網絡(GNN)
圖神經網絡是一種直接在圖結構上運行的神經網絡。GNN 的一個典型應用是節點分類。本質上,圖中的每個節點都與一個標籤相關聯,我們的目的是預測沒有 ground-truth 的節點的標籤。
本節將描述 The graph neural network model (Scarselli, F., et al., 2009) [1] 這篇論文中的算法,這是第一次提出 GNN 的論文,因此通常被認為是原始 GNN。
在節點分類問題設置中,每個節點 v 的特徵 x_v 與一個 ground-truth 標籤 t_v 相關聯。給定一個部分標記的 graph G,目標是利用這些標記的節點來預測未標記的節點的標籤。它學習用包含鄰域信息的 d 維向量 h_v 表示每個節點。即:
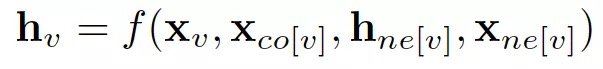
其中 x_co[v] 表示與 v 相連的邊的特徵,h_ne[v] 表示 v 相鄰節點的嵌入,x_ne[v] 表示v 相鄰節點的特徵。函數 f 是將這些輸入映射到 d 維空間上的過渡函數。由於我們要尋找 h_v 的唯一解,我們可以應用 Banach 不動點定理,將上面的方程重寫為一個迭代更新過程。
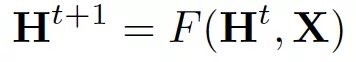
H 和 X 分別表示所有 h 和 x 的串聯。
通過將狀態 h_v 和特性 x_v 傳遞給輸出函數 g,從而計算 GNN 的輸出。

這裡的 f 和 g 都可以解釋為前饋全連接神經網絡。L1 loss 可以直接表述為:
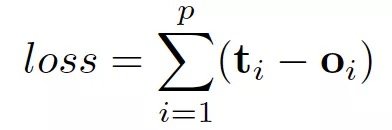
可以通過梯度下降進行優化。
然而,原始 GNN 存在三個主要局限性:
- 如果放寬 “不動點” (fixed point)的假設,那麼可以利用多層感知器學習更穩定的表示,並刪除迭代更新過程。這是因為,在原始論文中,不同的迭代使用轉換函數 f 的相同參數,而 MLP 的不同層中的不同參數允許分層特徵提取。
- 它不能處理邊緣信息 (例如,知識圖中的不同邊緣可能表示節點之間的不同關係)
- 不動點會阻礙節點分布的多樣性,不適合學習表示節點。
為了解決上述問題,研究人員已經提出了幾個 GNN 的變體。不過,它們不是本文的重點。
DeepWalk:第一個無監督學習節點嵌入的算法
DeepWalk [2] 是第一個提出以無監督的方式學習節點嵌入的算法。
它在訓練過程中非常類似於詞彙嵌入。其動機是 graph 中節點和語料庫中單詞的分布都遵循冪律,如下圖所示:
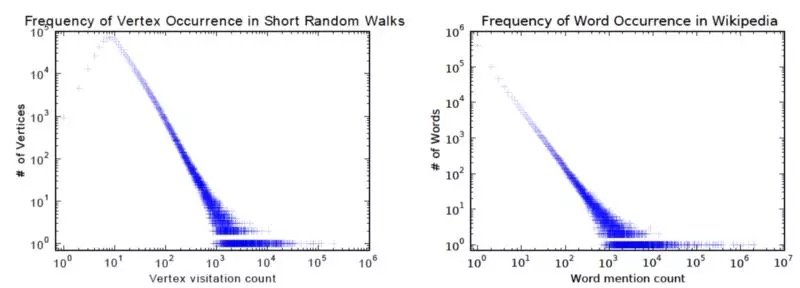
該算法包含兩個步驟:
- 在 graph 中的節點上執行 random walks,以生成節點序列
- 運行 skip-gram,根據步驟 1 中生成的節點序列,學習每個節點的嵌入
在 random walks 的每個時間步驟中,下一個節點從上一個節點的鄰節點均勻採樣。然後將每個序列截斷為長度為 2|w| + 1 的子序列,其中 w 表示 skip-gram 中的窗口大小。
本文採用 hierarchical softmax 來解決由於節點數量龐大而導致的 softmax 計算成本高昂的問題。為了計算每個單獨輸出元素的 softmax 值 , 我們必須計算元素 k 的所有 e ^ xk。

因此,原始 softmax 的計算時間為 O(|V|),其中 V 表示圖中頂點的集合。
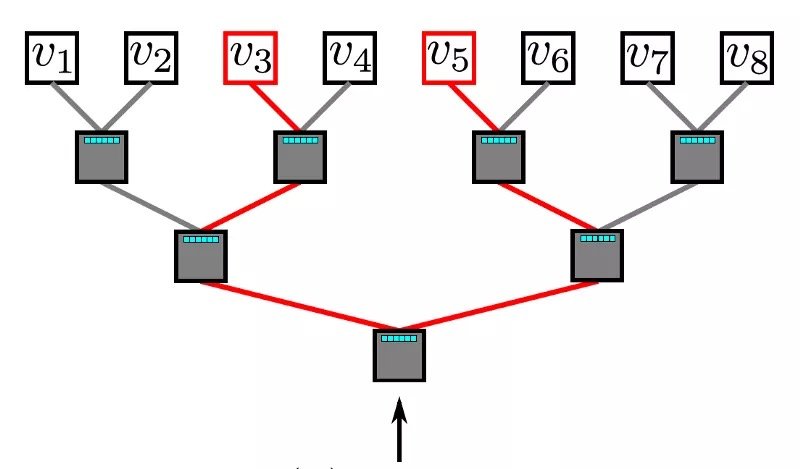
分層 softmax 利用二叉樹來處理這個問題。在這個二叉樹中,所有的葉子 (下圖中的 v1, v2,…v8) 都表示 graph 中的頂點。在每個內部節點中,都有一個二元分類器來決定選擇哪條路徑。要計算給定頂點 v_k 的概率,只需計算從根節點到葉節點 v_k 路徑上每一個子路徑的概率。由於每個節點的子節點的概率之和為 1,所以所有頂點的概率之和為 1的特性在分層 softmax 中仍然保持不變。由於二叉樹的最長路徑是 O(log(n)),其中 n表示葉節點的數量,因此一個元素的計算時間現在減少到 O(log|V|)。
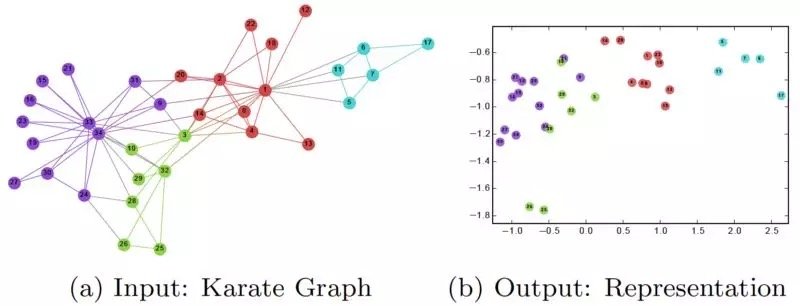
在訓練完 DeepWalk GNN 之後,模型已經學習了每個節點的良好表示,如下圖所示。不同的顏色表示輸入圖中的不同標籤。我們可以看到,在輸出圖 (2 維嵌入) 中,具有相同標籤的節點被聚集在一起,而具有不同標籤的大多數節點都被正確地分開了。
然而,DeepWalk 的主要問題是缺乏泛化能力。每當一個新節點出現時,它必須重新訓練模型以表示這個節點。因此,這種 GNN 不適用於圖中節點不斷變化的動態圖。
GraphSage:學習每個節點的嵌入
GraphSage 提供了解決上述問題的辦法,以一種歸納的方式學習每個節點的嵌入。
具體地說,GraphSage 每個節點由其鄰域的聚合 (aggregation) 表示。因此,即使圖中出現了在訓練過程中沒有看到的新節點,它仍然可以用它的鄰近節點來恰當地表示。
下面是 GraphSage算法:

外層循環表示更新迭代的數量,而 h ^ k_v 表示更新迭代 k 時節點 v 的潛在向量。在每次更新迭代時,h ^ k_v 的更新基於一個聚合函數、前一次迭代中 v 和 v 的鄰域的潛在向量,以及權重矩陣 W ^ k。
論文中提出了三種聚合函數:
1. Mean aggregator:
mean aggregator 取一個節點及其所有鄰域的潛在向量的平均值。
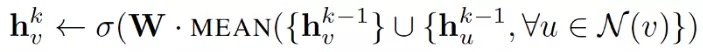
與原始方程相比,它刪除了上面偽代碼中第 5 行中的連接運算。這種運算可以看作是一種 “skip-connection”,在論文後面的部分中,證明了這在很大程度上可以提高模型的性能。
2. LSTM aggregator:
由於圖中的節點沒有任何順序,因此它們通過對這些節點進行排列來隨機分配順序。
3. Pooling aggregator:
這個運算符在相鄰集上執行一個 element-wise 的 pooling 函數。下面是一個 max-pooling 的示例:
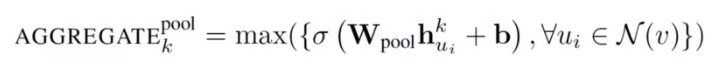
論文使用 max-pooling 作為默認的聚合函數。
損失函數定義如下:
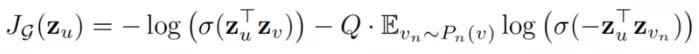
其中 u 和 v 在固定長度的 random walk 中共存,而 v_n 是不與 u 共存的負樣本。這種損失函數鼓勵距離較近的節點具有相似的嵌入,而距離較遠的節點則在投影空間中被分離。通過這種方法,節點將獲得越來越多的關於其鄰域的信息。
GraphSage 通過聚合其附近的節點,可以為看不見的節點生成可表示的嵌入。它允許將節點嵌入應用到涉及動態圖的域,其中圖的結構是不斷變化的。例如,Pinterest 採用了GraphSage 的擴展版本 PinSage 作為其內容發現系統的核心。
總結
本文中,我們學習了圖神經網絡、DeepWalk 和 GraphSage 的基礎知識。GNN 在複雜圖結構建模方面的強大功能確實令人驚嘆。鑒於其有效性,我相信在不久的將來,GNN將在 AI 的發展中發揮重要作用。
[1] Scarselli, Franco, et al. “The graph neural network model.”http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.7227&rep=rep1&type=pdf
[2] Perozzi, Bryan, Rami Al-Rfou, and Steven Skiena. “Deepwalk: Online learning of social representations.”http://www.perozzi.net/publications/14_kdd_deepwalk.pdf
[3] Hamilton, Will, Zhitao Ying, and Jure Leskovec. “Inductive representation learning on large graphs.”https://www-cs-faculty.stanford.edu/people/jure/pubs/graphsage-nips17.pdf
本文轉自公眾號 新智元,原文地址



Comments