循環神經網路產生動機
假設我們現在使用傳統的語言模型來做一個簡單的預測任務,存在這樣一個句子:
讀芯術是一個優秀的公眾號,裡面有著很多有用的信息,我經常在___中尋找信息、獲取知識。
如果我們採用n-gram模型去預測空格的內容,比如2-gram,模型會給出「在」之後出現概率最高的詞。雖然在我們看來,「讀芯術」是高概率的選項,但在訓練了很多資料後,「讀芯術」出現在「在」的後面概率必然是極低的,因為我們一般會說「在家」等常用詞。當然,我們可以將模型看到的範圍繼續擴大,直到在前文中看到讀芯術這個名稱,但是這樣的思路在實踐中並不可行,N越大,馬爾可夫鏈就越長,數據稀疏嚴重,計算困難,更重要的是,我們需要將這個N設定為一個固定的值,這樣就無法處理任意長度的句子。
帶有循環結構的網路都可以被叫做循環神經網路(recurrent neural network),RNN可以非常有效的解決這個問題,從簡單的理論上來說,它可以處理任意長度的序列,並且不需要提前將N固定住,靈活性更高。
卷積神經網路也可以處理時間序列的問題,尤其是在我們關心某些特徵是否出現,而不是它具體位置的時候,CNN具有一定的優勢。但在處理自然語言類型的數據時,比如在情感分類問題中,我們將文本分成正面和負面,CNN在可能會處理成某些詞語的出現就意味著正面情感,比如「喜歡」,「美」,如果這樣一個句子:
我不是不喜歡這部電影,這部電影不能說不美,但是……
我們能很快的知道,這個評價是一個負面評價。那麼如果只提取特徵,而忽略了詞與詞之間的關係,CNN可能會發現文本存在「喜歡」就將其歸為正面,看到「不喜歡」就歸為負面,再看到「不是不喜歡」就又將其歸為正面,顯然是不合理的。這時就需要我們採用語言模型來理解這句話的意思。
理解循環神經網路
我們經常會在學習資料中見到RNN的圖示:

這幅圖對於初學者來說是不友好的,而且非常容易產生更多的誤解,雖然我們能從中看到時間序列的依賴性,從st-1到st中添加了傳播的箭頭,表示有信息從前面的神經元直接流向後面的神經元,但關於更多問題是這張圖無法告訴我們的,比如:
- 數據是同時進入的嗎?
- 在最開始的時候,第一個單元是否也會接受前一個神經元的輸入?如果是,第一個神經元沒有前一個神經元,那麼這個輸入來源於哪裡?
- 在同一層的隱藏單元中進行傳播的權值矩陣W,以及輸入到隱層的權值矩陣U,隱層到輸出的權值矩陣V,為什麼是相同的?
雖然上圖是一個使用廣泛的示意圖,事實上,更好理解循環結構的方式並非如此。
為了更好的幫助大家理解循環結構,我畫了幾幅草圖。設想一個簡單的前饋神經網路,輸入、輸出、隱層均只有一個神經元,如下圖。這裡的圓圈沒有任何抽象的含義,一個圓圈就是一個神經元:
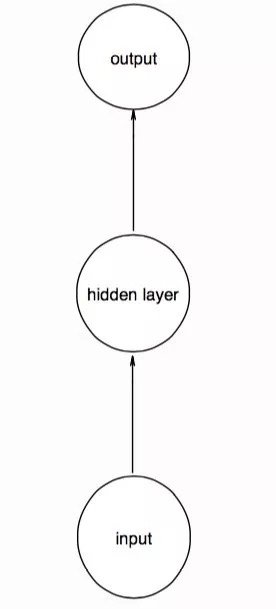
當我們輸入時間序列的第一個數據點後,就把這時隱層的值用一個記憶單元存起來,這個記憶單元並不是一個實體,而是一個用來存取東西的結構:
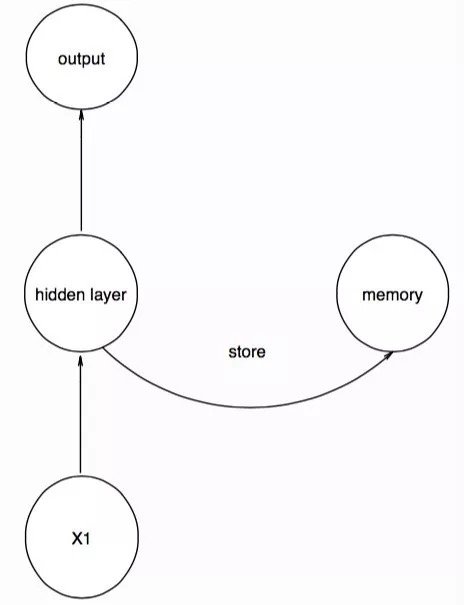
我們存入的memory單元的作用就存取了X1的特徵,當我們輸入時間序列的第二個數據點時,要注意,網路的結構保持不變,只是我們將memory中的信息也輸入到隱層中,相當於,第二個數據點的隱層接受了數據和第一個數據點的特徵進行輸出,同時將此時隱層的信息返回到memory,再次存起來:
在第三個數據點輸入的時候,memory單元所操作就是前一步得到的信息,並將得到的信息存起來,供下一個時間步的輸入:

這樣依次進行下去,我們就得到了與大家喜聞樂見的那幅圖類似的結構,為了表達先前的信息對現在的影響,我們在輸入memory單元時,採用一個權值矩陣W參數化記憶單元,那麼一一對應關係就變成了:
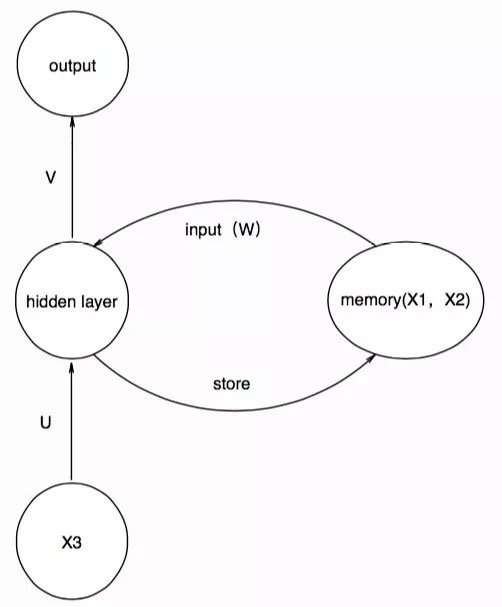
在這裡,我們將每個圓圈都理解為一個神經元,但如果我們將一個圓圈理解為一層神經元,也就是將其抽象成結構,輸入,隱層,輸出都是多維的,並將其按照時間展開,就會得到:
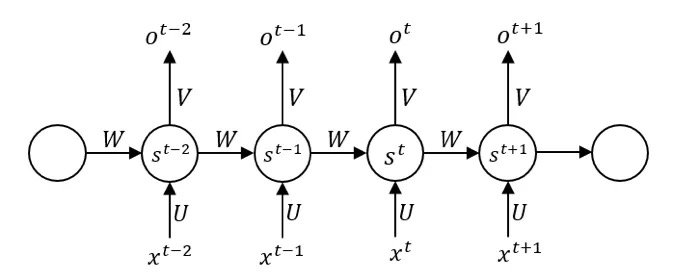
在此基礎上,我們解釋上述的問題:
- 數據是同時進入的嗎?顯然不是,數據是按照順序進入,我們在處理序列化的數據時,往往會在用滑動窗口的辦法來調整不同的結構。
- 在最開始的時候,第一個單元是否也會接受前一個神經元的輸入?如果是,但第一個神經元沒有前一個神經元,那麼這個輸入來源於哪裡?
我們在第一個數據點進入時,需要對memory單元設置初始值,這個初始值可以作為一個參數,也可以將其簡單的設置為零,表示前面沒有任何信息。 - 在同一層的隱藏單元中進行傳播的權值矩陣W,以及輸入到隱層的權值矩陣U,隱層到輸出的權值矩陣V,為什麼是相同的?
這是一個非常重要的問題,也是我們無法從圖中推斷的知識。大大減少參數數量是一個原因,但不是本質上的。我們先不考慮矩陣W,只考慮普通的神經網路,因為在序列上不同數據,都是採用相同的神經網路。CNN用參數共享的卷積核來提取相同的特徵,在RNN中,使用參數共享的U,V來確保相同的輸入產生的輸出是一樣,比如一段文本中,可能會出現大量的「小狗」,參數共享使得神經網路在輸入「小狗」的時候,產生一樣的隱層和輸出。
此時,我們討論矩陣W,參數共享的矩陣W確保了對於相同的上文,產生相同的下文。




Comments