本文轉載於公眾號 讀芯術,原文地址
在上一節(如何理解RNN?(理論篇))的課程我們介紹了循環神經網路的基本結構,同時這樣的循環結構也會給優化帶來一定的困難,本文主要介紹兩種較為簡單的方式來緩解RNN的優化問題:
- 正交初始化
- 激活函數的選擇
BPTT的兩個關鍵點
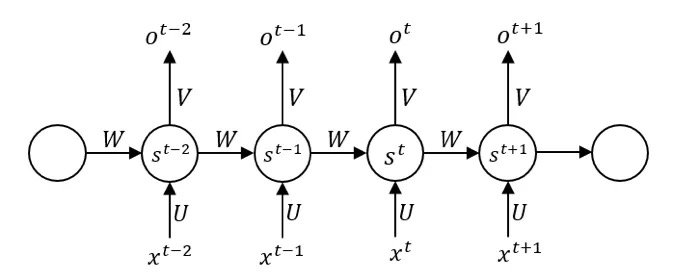
我們可以上圖寫出前向傳播的公式,使用f作為隱藏單元的激活函數,g作為輸出單元的激活函數,為了簡化問題,不使用偏置,也不在單元中使用閾值,一個圓圈只代表一個神經元,以St為例:
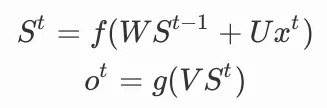
其中:
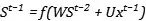
在反向傳播時,我們就不能採取原來逐層反向傳播的方法去更新參數,因為數據在使用時有著不同的進入順序,同時每個時間步共享參數,我們對單獨時間步的更新需要考慮整個序列上的信息。我們稱這樣的方式為沿時間的反向傳播(BP through time),但真正本質的機制只有兩個,參數共享和循環結構。
要理解這一點並不難,我們只需要考慮矩陣乘法,參數未被共享的情況下,從形式上來看,矩陣參數更新之間互不干擾,我們可以很方便對每個參數進行更新,但如果參數共享,那麼矩陣的元素需要綁定在一起更新,梯度的更新變為了參數共享的區域梯度之和。因為參數共享的區域是沿著時間共享,所以求和也需要按照時間。(在同樣具備參數共享的CNN的反向傳播中,求和是按照空間)
我們對參數V的更新,就要考慮不同時間步上的參數共享,我們可以把前向傳播寫成矩陣的形式:
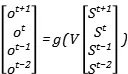
就有:
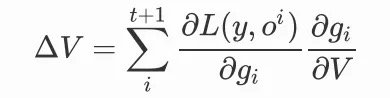
在此基礎上,我們對於參數U進行同樣的前向傳播操作:
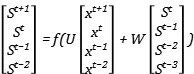
我們會發現,當前時間步的變數St會包含前一步的變數St-1,此時我們選擇對U或者W求梯度,就不能忽略掉前一步的變數,因為前一步的變數中也包含了參數U和W,那麼我們在對U進行更新時,就需要將前面的時間步遞歸展開:
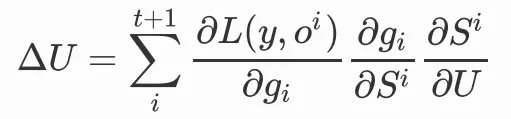
因為:
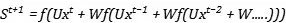
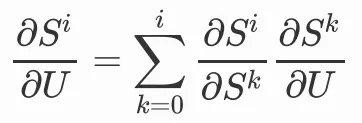
同理,我們對W做參數更新,也是同樣的結構:
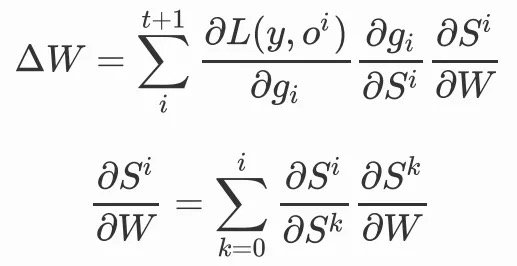
我們可以清晰的看到,權重共享機制使得我們需要對每個時間步梯度求和,循環結構使得我們需要遞歸地處理梯度,根據我們的展開式,每一個
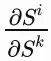
都會產生一個或多個W,比如:
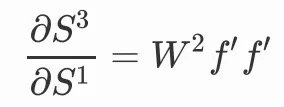
當我們鏈的越來越長的時候,整條鏈出現了W的連乘,這正是循環結構帶來的。
在普通的神經網路中,梯度消失往往來源於激活函數和層與層協調更新,但在RNN中,梯度消失和爆炸的來源之一就是共享參數W的連乘。在RNN中,循環層如果沒有梯度的流動,那麼就表示序列的信息並沒有傳達到下去,我們所謂的記憶單元就會喪失記憶能力,RNN相比傳統n-gram模型的優勢也就不復存在。
從理論上來說,我們希望儘可能保持W值保持在一定範圍內,使得網路可以被有效的訓練。
正交初始化
正交初始化的思路很簡單,就是利用了正交矩陣的性質,它的轉置矩陣就是它的逆矩陣,有:
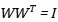
使得矩陣的連乘不會放大或者縮小W本身的值。
我們也可以從另外一個角度來理解,如果我們對矩陣做特徵值分解,分解為對角矩陣和正交矩陣的乘積:
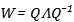
矩陣的連乘就會變成:
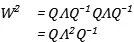
矩陣的連乘就會變為其特徵值的連乘,所以:
• 如果特徵值的絕對值都小於1,那麼參數梯度會越變越小。
• 如果特徵值近似都等於1,那麼參數梯度就可以保持正常範圍。
• 如果特徵值的絕對值都大於1,那麼參數梯度會越來越大。
正交矩陣的特徵值要麼是1、要麼是-1,雖然我們無法保證參數矩陣W永遠都是這樣的形式,但至少可以在初始化上做到這一點。
激活函數
我們很早就曾講過激活函數的重要性,sigmoid函數具有非中心化和廣泛的飽和性,ReLU以及它的各種變體可以很好的解決這個問題,但是在循環神經網路中,我們需要考慮參數的特徵值,ReLU在其右端是一個線性函數,雖然它的梯度恆定為1,但函數值卻可以無限的增長。
傳統的ReLU在RNN中則可能會帶來梯度爆炸的問題,但解決梯度爆炸我們一般會採用截斷(clipping)的方式,也就是如果梯度大於某值,就令其等於某值。另外,我們還可以在採用tanh激活函數,因為它的範圍在[-1,1],更好的適應參數連乘帶來的梯度爆炸,卻也在一定程度上無法避免梯度消失。
我們需要在這兩者之間做trade-off,因為我們既不想讓激活函數對權重求導的部分變得太大或者太小,也不希望函數本身的值變得太大或者太小。



Comments