在解释分类指标之前的一个关键概念是该过程如何工作。你有三个数据集。它们是训练集，验证集和测试集。

  1. 训练集：使用训练集中的数据构建模型。您，模型，从此数据集中的输入中学习。
  2. 验证集：有几种方法可以获得验证集。一种简单的方法是删除部分数据并将其作为验证集。因此，当您训练模型时，模型尚未从验证集中学习。验证集指示您的训练集的执行情况。您还可以使用验证集调整超参数，因为您知道正确的答案。
  3. 测试集：测试集通常远不及数据科学家。在此步骤中测试我们的模型表明我们的模型执行得有多好。

我在Jupyter Notebook中创建了一个随机数据帧。我们在验证集中。我们的客户将为我们提供一个新的数据集（测试集）。我们的目标是获得最佳表现。

你的表现是什么意思？

我将演示我们的分类模型如何衡量绩效。在决定如何衡量绩效时存在细微差别。但首先，让我们创建一个0和1的数据帧。

我们还需要知道这些定义：

  1. 真实肯定：准确预测的总数是“正面”。在我们的示例中，这是正确预测电子邮件为垃圾邮件的总数。
  2. 误报：“肯定”的不准确预测总数。在我们的示例中，这是错误地将电子邮件预测为垃圾邮件的总数。
  3. 真实否定：“否定”的准确预测总数。在我们的示例中，这是正确预测电子邮件为非垃圾邮件的总数。
  4. 错误否定：“否定”的不准确预测总数。在我们的示例中，这是错误地将电子邮件预测为非垃圾邮件的总数。

为了获得这些指标的出色视觉效果，我们将使用混淆矩阵。在Python中，sklearn库使得创建混淆矩阵非常容易。

如果我们回顾一下定义：

  1. 真实的积极因素：238
  2. 误报：19
  3. 真正的否定：219
  4. 假阴性：24

“这是伟大的亚历克斯，但还没有讨论过表现！”

正确。但我们现在有了继续进行的信息。我将解释准确度，精确度，召回率（灵敏度），F1分数，特异性，对数损失和ROC / AUC曲线。

准确性

式：

  • 正确/预测＃的数量
  • （TP + TN）/（TP + FP + TN + FN）

准确性似乎可能是最好的方法。在我们的例子中，我们的准确率为91.4％。得分很高。那么为什么不使用呢？

我的想法：

  • 准确性仅在两种可能的结果（电子邮件是否为垃圾邮件）相等时才有效。例如，如果我们有一个数据集，其中5％的电子邮件是垃圾邮件，那么我们可以遵循不太复杂的模型并获得更高的准确度分数。我们可以将每封电子邮件预测为非垃圾邮件，并获得95％的准确度分数。不平衡数据集可以提供准确性，而不是可靠的性能指标。解释的悖论是指“ 准确性悖论 ”，

精密/召回

这两个性能指标经常结合使用。

精确

式：

  • TP /（TP + FP）

精确地说，我们通过“积极”预测的表现来评估我们的数据。我们对电子邮件示例的精确度为92.61％！请记住，我们示例中的“正面”是预测电子邮件是垃圾邮件。

考虑精确积极预测的准确性。

召回（也称为灵敏度）

式：

  • TP /（TP + FN）

通过召回，我们通过其积极成果的基本事实的表现来评估我们的数据。意思是，当结果为正时，我们判断预测为正。我们对电子邮件示例的召回率为90.83％！

我的想法：

  • 你不可能拥有两全其美的优势。在我们的电子邮件示例中，我们具有高精度和召回分数。但是，需要权衡利弊。想一想。精度的分母是TP + FP。它不考虑FN。因此，如果我们只做了一个正面预测，并且是正确的，那么我们的精确分数将是1.尽管如此，我们可能错过了许多实际的积极观察。
  • 另一方面，Recall的分母是TP + FN。它没有看到我所做的所有自信预测。我们可以预测所有电子邮件都是垃圾邮件。因此，我们将Recall评分为1，因为我们预计每个例子都是正数，而我们的FN将为0（我们不预测非垃圾邮件）。

此外，它取决于你是否应该使用精确或召回的情况。在某些情况下，您最好采用高召回率。

  • 如果您将每封电子邮件标记为垃圾邮件，则会召回1.为什么？因为您预测电子邮件是垃圾邮件。由于您没有预测电子邮件是非垃圾邮件，因此您无法使用假阴性。但是，您也会错误地将垃圾邮件预测为非垃圾邮件。
  • 如果您预测一封电子邮件是垃圾邮件，并且您做得对，那么您的精确度将是1.为什么？因为没有误报。但是，你会遗漏很多预测。

还有一个不太常见的性能指标：特异性。

特异性与Sensitivity或Recall相反。因此，公式为TN /（TN + FP）。

F1-分数

“F 1 Score是Precision和Recall的加权平均值。因此，该分数考虑了误报和漏报。直觉上它并不像准确性那么容易理解，但F1通常比准确性更有用，特别是如果你有不均匀的类分布。“ – Renuka Joshi

式：

  • （2 *（精确*召回））/（精确+召回）

F1-Score是精确度和召回率的加权平均值（调和平均值）。我们的F1分数为91.71％。

ROC曲线 / AUC评分

的ROC曲线（ROC曲线）是示出分类模型中的所有分类的阈值的性能的曲线图。

AUC代表“ROC曲线下的面积”。也就是说，AUC测量从（0,0）到（1,1）的整个ROC曲线下面的整个二维区域（认为积分微积分）。

当我们评估模型时，ROC曲线/ AUC分数最有用。让我解释。我们的基本事实和预测是1和0。但是，我们的预测从不是1或0.相反，我们预测概率，然后评估它是1还是0.通常，分类阈值是.5（在中间）。但我们可以有更好的分类门槛。

我们的ROC曲线所关注的指标是TPR（真实正率）和FPR（误报率​​）。

  • 真阳性率：TP /（TP + FN）
  • 误报率：FP /（FP + TN）
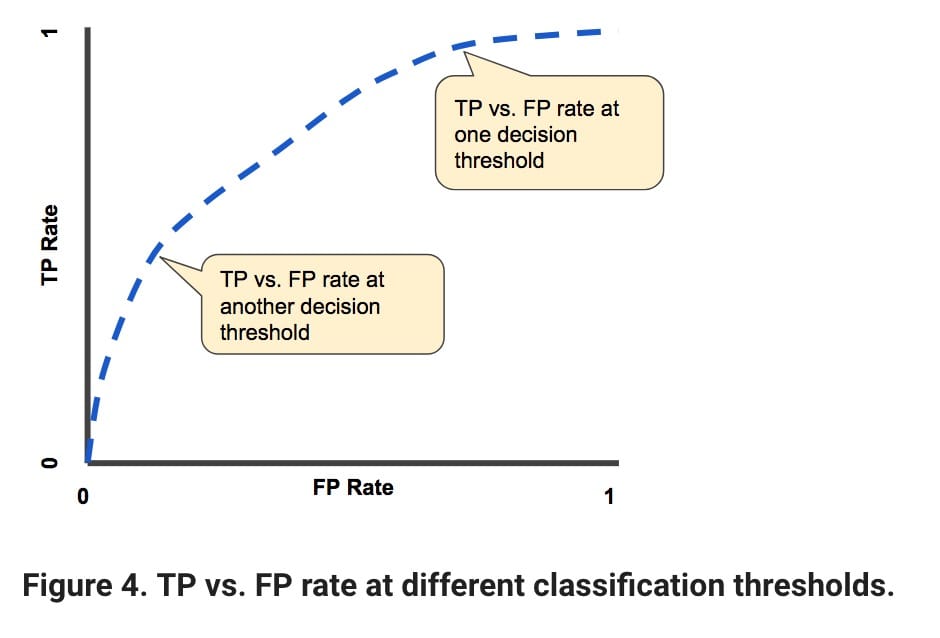
资料来源：https：//developers.google.com/machine-learning/crash-course/classification/roc-and-auc

我们对ROC的目标是使下图中的蓝线尽可能接近图的右上部分。另一方面，它越接近直线，我们的模型性能越差。红点代表了TPR和FPR之间的权衡。

  • 如果您正在与癌症患者打交道，那么获得高TPR比FPR更重要。您想要准确地检测尽可能多的癌症患者。你的假阳性率很高并不重要。
  • 如果您需要将误报率保持在较低水平，假设您不希望对某些人产生偏见，则还必须接受较低的真实正面率。

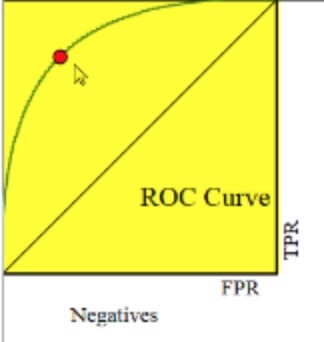
AUC是曲线下面积。因此，它将是一个介于0和1之间的数字。我们希望它能够接近1。

我知道这个例子在比较模型时没用，但重要的是要知道！

登入损失

对数损失根据与实际标签的差异程度来考虑预测的不确定性。这使我们对模型的性能有了更细致的了解。

式：

  • – （ylog（p）+（1-y）log（1-p））

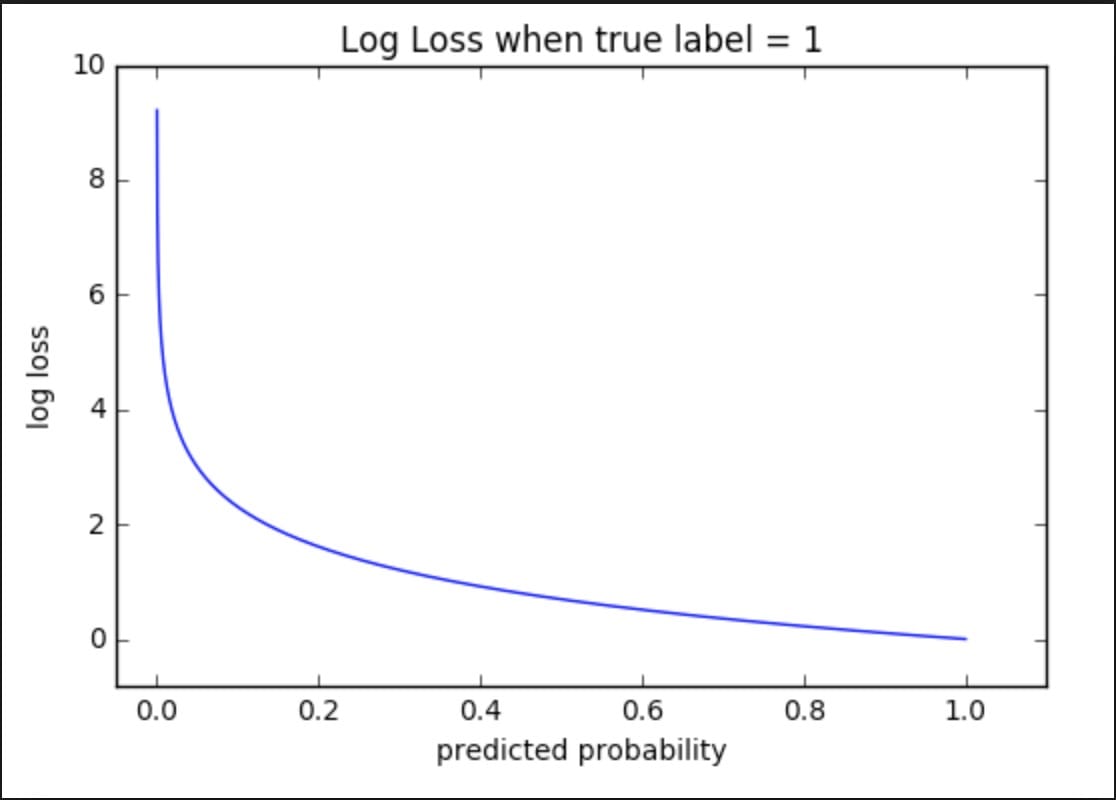
对于对数丢失，我们使用我们预测的概率。

我们来看看上面的图表。注意它是如何说明“真正的标签= 1”。那么，这表明了基本事实。此外，该数字的斜率是显着的。当预测概率接近0时，我们的对数损失呈指数增长。而在另一端，日志损失接近0。

直觉也适用于“真实标签= 0”，除了图表是水平反射，我们看到指数增长为1而不是0。

现在，它想评估每个分类标签（多类）和每个例子的性能，公式如下：

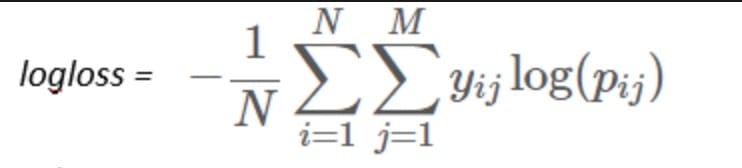
多级对数损失

结论

我希望您能够直观地了解这些不同的性能指标。只需在Kaggle从事数据科学项目以获得实际的理解！