本文轉載自公眾號 讀芯術，原文地址

RNN的訓練有別於普通前饋神經網路，反向傳播中會產生權重矩陣的連乘，使得長時間步下的微弱偏移得到放大，產生梯度消失和爆炸，上文介紹的正交初始化和激活函數的選擇，目的都是讓參數矩陣的特徵值盡量維持在1附近。我們本文介紹一種「曲線救國」的方式，它並不直接改變權重的特徵值，而是將神經元參數化，通過生成線性自循環的路徑，取消了原本RNN中的權重參數W，這就是長短時記憶單元LSTM（long short-term memory）。

這裡面有一個廣泛的誤解，這個單元並不是擁有長時記憶和短時記憶的單元，而是一個長的短時記憶單元，短時記憶在心理學上就表示著工作記憶，類似於內存。從英文名字可以看出來，是long short-term memory，而非long-short term memory。

我們在之前的《如何理解神經網路的循環結構》中曾經闡明了循環結構的本質，它對於不同時間步上的數據序列使用了同樣的網路結構，只是將某個或者幾個層存儲起來用作下一時間步的輸入，這個存儲的結構就是記憶單元：

如圖為RNN的簡單結構，我們依次輸入序列化數據，前一個時間步的隱層會將得到的數據存放到memory單元，然後再將memory單元乘以矩陣W進入到下一個時間步的隱層。

在上圖中，我們下一個時間步的memory單元的存儲的信息（Ct）就是：

我們取消權重參數W，並對這個memory單元做重參數化：

  • 由一個門（gate）來參數化存儲的步驟，當這個門打開時，我們才會將信息存放到memory單元，這個門叫做輸入門（Input Gate）。
  • memory單元要不要將信息流入到下一個時間步，也由一個門控制，只有當這個門打開時，我們才會將信息輸入到下一個時間步，這個門叫做輸出門（Output Gate）。

memory單元並非是一個實體，完全可以嵌入到隱藏層本身，我們在這個操作之上又增添了兩個門，用來控制輸入和輸出，就得到了一個基本結構： 

其中，輸入和輸出由sigmoid函數控制，sigmoid函數的輸出在[0,1]，可以很好的刻畫門的開啟或者關閉狀態，值的大小就可以表示門被開啟的程度。我們將輸入門的結果用一個函數Fi來表示，輸出門的結果用Fo來表示，為了保證輸入門的開啟和關閉狀態對輸入的影響，我們將其直接相乘再一起進入memory，memory的狀態我們用C來表示：

這樣存入到memory的值就受到了輸入門的調節，當其完全關閉時，就代表著信息沒有流入。接下來，在輸出的時候，我們再次相乘輸出門的結果，但是，如果我們希望輸入門和輸出門的儘可能獨立一些，因為直接相乘必然會導致當輸入門很小時，輸出門即便很大，也不會產生多少輸出，所以，我們使用一個函數g作用在memory的結果上，再進行輸出門的控制處理：

此時我們得到了一個較為複雜的神經元，輸入門控制了信息的流入，輸出門控制了信息的流出，那麼看起來我們的memory單元是不必要的，但是在RNN中，我們必然採用權重W來控制流通的信息，在LSTM中，我們並沒有使用權重，而只是採用簡單的相加：

隨著序列越來越長，時間步越來越大，前一步的memory會流入到我們下一步的memory，會使得後面的memory單元存儲的數值越來越大。此時，有兩種可能的後果：

  • 如果我們的函數g也是一個帶有擠壓性質的激活函數，那麼過大的值將會使得這個激活函數永遠處於激活狀態，失去了學習能力。
  • 如果我們的函數g是ReLU類型的函數，值變得非常巨大時，會使得輸出門失效，因為輸出門的值再小，當它乘以一個龐大的值時，也會變的非常大。

無論是哪種情況，都在表明我們需要在memory單元中丟棄一些信息，LSTM的解決辦法是在原本的單元中加入一個遺忘門（forget gate）,它的作用是重參數化記憶單元，將記憶單元輸入的信息乘以遺忘門的結果Ff，存入到記憶單元中作為信息，所以當前的信息就變為了：

可以寫出公式如下：

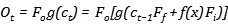
需要特別注意的是，如果我們使用sigmoid函數作為激活函數，那麼當遺忘門為1時，就代表著將前一步的信息原封不動的存入到當前，這與它的名字恰好相反，也就是說，當遺忘門關閉時，它會忘記，當遺忘門打開時，它才會回憶。（有點拗口）

整個流程就是，我們將當前時間步的數據乘以輸入門的結果，同時前一步的記憶單元乘以遺忘門的結果，兩者相加，一起乘以輸出門的結果，得到下一層的輸出，同時此時的記憶單元參與到下一時間步的運算。

這是一幅大家喜聞樂見的LSTM的示意圖，如果你看懂了前面的內容，那麼可以和我一起來走一遍，1代表著遺忘門，2代表著輸入門，3代表著輸出門，中間的符號有➕，✖️，就代表著兩種運算，從左到右，上一步的記憶單元C（t-1）與遺忘門相乘，再加上輸入門與輸入的相乘結果得到當前的記憶單元Ct，Ct沿箭頭參與到下一時間步的記憶運算。同時Ct與輸出門相乘得輸出Ht，Ht沿著箭頭參與到下一時間步的輸入運算。

在理解LSTM的工作流程之後，我們自然會問它是如何解決長期依賴的問題，有的人會認為這是因為它包含了短時記憶和長時記憶，有的人則會看圖說話，說這是因為上一層的信息無損的流入下一層。這兩種說法都是錯誤的。

真正的答案就在上文的取消權重W。在普通RNN中，隨著時間步，同一記憶單元存儲的信息會越來越多，就選擇使用一個權重參數W來學習到自己保留或者去除掉哪些信息，但卻會帶來長期依賴的問題。整個LSTM的最精華的部分是遺忘門的設計，它不通過權重W就可以解決掉信息冗餘的問題，由

變為了

當遺忘門打開時，接近於1，在反覆傳播中就以更小的幾率產生梯度消失。在實踐中，我們往往也要保證遺忘門在大多數時間上是被打開的。