上一篇:《為建模做好數據準備:特徵工程,特徵選擇,降維(第1部分》
一旦有了足夠的數據,就可以選擇特徵選擇或特徵提取(它們大部分都可以完成相同的工作,並且可以互換使用)。通常有兩種方法:
- 特徵提取/選擇
- 降維或特徵減少
讓我們一步一步地找出它們。
第2部分:特徵提取/選擇
那麼什麼是特徵選擇?特徵提取?他們的區別?
→在機器學習和統計中,特徵選擇(也稱為變量選擇)是選擇相關特徵子集(變量,預測變量)以用於模型構建的過程。
→特徵提取用於創建一組新的較小的特徵,這些特徵仍會捕獲大多數有用的信息。
→同樣,特徵選擇保留原始特徵的子集,而特徵提取則創建新特徵。
特徵選擇/提取的重要性
→當功能數量很大時,這一點變得尤為重要。
→您無需使用所有可用功能來創建算法。
→您可以通過僅提供真正重要的功能來輔助算法。
在哪裡使用功能選擇?
→它使機器學習算法的訓練速度更快,降低了複雜度並使其更易於解釋。
→如果選擇了正確的子集,則可以提高模型的準確性。
→這樣可以減少過度擬合的情況。
它可以大致分為兩種技術(儘管這不是「 那裡的唯一方法 」)
一世。單變量特徵選擇
ii。多元特徵選擇
ünivariate功能選擇:該技術涉及多個手工樣的工作的。訪問每個功能並與目標一起檢查其重要性。為了實施「單變量特徵選擇」 ,您應該掌握一些技巧。
→如果您具有適當的領域知識並信任您的判斷電話,則始終從此步驟開始。分析所有功能並刪除所有不需要的功能。是的,這是耗時費力的步驟,但是,嘿,您會更信任的人,「機器還是您自己」
→ 檢查所有功能的方差(是的,一直是令人困惑的偏差方差折衷:)。此處的經驗法則規則設置了一個閾值(例如,方差為0的特徵表示每個樣本具有相同的值,因此該特徵不會給模型帶來任何預測能力)相應地刪除特徵。
→ 皮爾遜相關係數的使用:這可能是三種方法中最適用的技術。如果您不了解或困惑,請先閱讀本文。
- 簡而言之,它為我們提供了目標變量和功能之間的相互依存關係。

- 使用Pearson相關的Thumb規則:
一世。只選擇與目標變量的中等至強關係。(請參見上圖)。
ii。當兩個要素本身與目標變量之間具有很強的關係時,則選擇它們中的任何一個(選擇兩者都不會增加任何值)。使用「 seaborn.heatmap() 」進行可視化和選擇,這很有幫助。
iii。這裡有個陷阱。它對線性數據最有效,而對非線性數據則效果較差(因此請避免使用)。
中號ultivariate功能選擇:當你有很多的功能(如他們的數百或數千個),那麼它真的成為不可能去和手動檢查他們中的每一個,或者如果你沒有足夠的領域知識,那麼你得相信以下技術。因此,用通俗易懂的術語講,就是一次選擇多個功能。
多元特徵選擇大致分為三類:

讓我們檢查一下(我們將討論每個類別中使用最廣泛的技術)
過濾方式:
→過濾方法通常用作預處理步驟。功能的選擇與任何機器學習算法無關。
→過濾器方法對功能進行一些排名。排名表示每個功能可能對分類有多「有用」。一旦計算出該排名,就創建了由最佳N個特徵組成的特徵集。
→在各種統計測試中,根據要素的得分選擇要素與結果變量的相關性。(此處的相關性是一個主觀術語)。

- 皮爾森的相關性:哦,是的!皮爾遜相關是過濾方法。我們已經討論過了。
- 差異 閾值:我們已經討論過了。
- 線性判別分析:目標是將數據集投影到具有良好類可分離性的低維空間上,以避免過度擬合(「 維數的詛咒 」)並降低計算成本。
→不進行數學運算,LDA將所有較高維度的變量(我們無法繪製和分析)帶到2D圖形上,同時這樣做會刪除無用的功能。
→LDA還是一種「 降低維數」技術,比「 選擇」更具特徵提取能力(因為它通過減小維數來創建新變量)。因此,它僅適用於標記的數據。
→最大限度地提高了類之間的可分離性。(技術術語過多,對。不用擔心,請觀看視頻)。
其他:
方差分析:方差分析它與LDA相似,不同之處在於它使用一個或多個類別獨立特徵和一個連續從屬特徵進行操作。它提供了幾個組的均值是否相等的統計檢驗。
卡方:這是一種統計測試,應用於分類特徵組,以使用它們的頻率分佈來評估它們之間相關或關聯的可能性。
應該記住的一件事是,濾波方法不會消除多重共線性。因此,在訓練數據模型之前,您還必須處理要素的多重共線性。

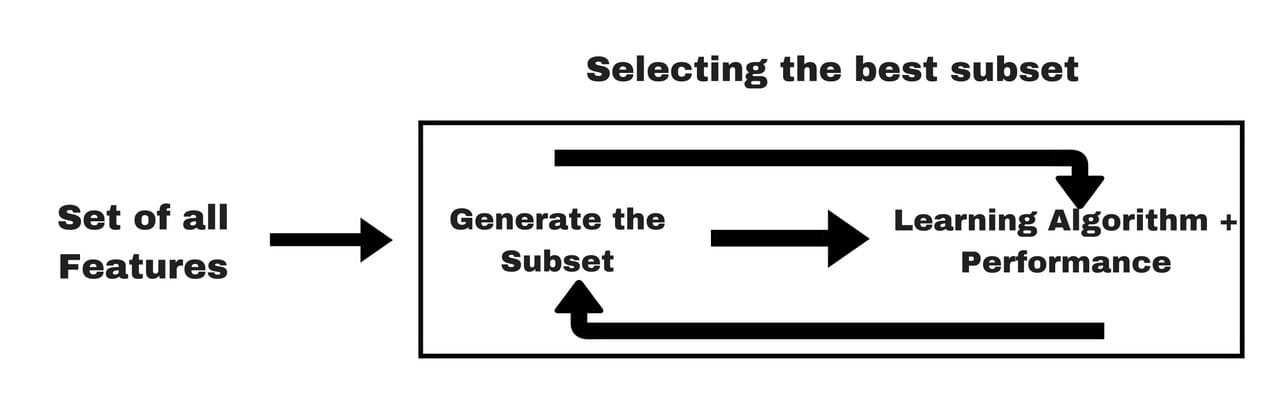
包裝方法:

→根據從先前模型得出的推論,我們決定從您的子集中添加或刪除特徵。
→之所以稱為包裝器方法,是因為它們將分類器包裝在特徵選擇算法中。通常,選擇一組功能。確定這套裝置的效率;進行一些更改以更改原始集,並評估新集的效率。
→這種方法的問題是特徵空間很大,查看每個可能的組合將花費大量時間和計算量。
→從本質上講,該問題已簡化為搜索問題。這些方法通常在計算上非常昂貴。
- 正向選擇:正向選擇是一種迭代方法,我們從模型中沒有任何特徵開始。在每次迭代中,我們都會不斷添加最能改善模型的功能,直到添加新變量不會改善模型的性能為止。
- 向後消除:在向後消除中,我們從所有特徵開始,並在每次迭代時都刪除最不重要的特徵,從而提高了模型的性能。我們重複此過程,直到在去除特徵方面未觀察到任何改善。
- 遞歸特徵消除(RFE):它通過遞歸刪除屬性並基於剩餘的屬性構建模型來工作。它使用外部估計器為要素(例如線性模型的係數)分配權重,以識別哪些屬性(以及屬性的組合)對預測目標屬性的貢獻最大。
→這是一種貪婪的優化算法,旨在找到性能最佳的特徵子集。
→它會反覆創建模型,並在每次迭代時保留性能最佳或最差的功能。
→它將構建具有左側特徵的下一個模型,直到用盡所有特徵。然後,根據特徵消除的順序對特徵進行排序。
# Recursive Feature Elimination from sklearn.feature_selection import RFE from sklearn.linear_model import LinearRegression# create a base classifier used to evaluate a subset of attributes model = LinearRegression()X, y = iowa.iloc[:,:-1], iowa.iloc[:,-1] # create the RFE model and select 3 attributes rfe = RFE(model, 10) rfe = rfe.fit(X, y)# summarize the selection of the attributes print(rfe.support_) print(rfe.ranking_) Output: [False False True True False False False False False False False False False False False True True True False True True True True False True False False False False False False False False False] [16 24 1 1 4 9 18 13 14 15 11 6 7 12 10 1 1 1 2 1 1 1 1 5 1 23 17 20 22 19 8 21 25 3]
→這就是以上示例中發生的情況,
一世。’ rfe.support_ ‘ 順序給出有關特徵的結果(顯然是基於所選模型,而沒有要求)。
ii。’ rfe.ranking_ ‘分別給所有特徵賦予等級。當您需要的功能多於您向「 n_features_to_select」輸入的功能時(例如上面的10個),這確實很方便。因此,您可以設置閾值並分別選擇其上方的所有功能。
4.順序特徵選擇器:順序特徵選擇算法是一系列貪婪搜索算法,用於將初始 d維特徵空間縮小為 k維特徵子空間(其中 k <d)。
→逐步進行功能選擇從評估每個單獨的功能開始,然後選擇那些性能最佳的選定算法模型。
→後退特徵選擇緊密相關,您可能已經猜到了,它從整個特徵集開始,然後從那裡進行反作用,刪除特徵以找到預定義大小的最佳子集。
→什麼是「最佳」?
這完全取決於定義的評估標準(AUC,預測準確性,RMSE等)。接下來,評估所選特徵和後續特徵的所有可能組合,並選擇第二個特徵,依此類推,直到選擇了所需的預定義數量的特徵。
→簡而言之,SFA會根據分類器的性能同時刪除或添加一個特徵,直到達到所需大小k的特徵子集為止。
注意:我建議您訪問官方文檔以通過示例更詳細地了解它
順序特徵選擇器— mlxtend一個由有用的工具和擴展組成的庫,用於日常數據科學任務。rasbt.github.io
嵌入方法:
→嵌入式方法結合了過濾器和包裝器方法的質量。它由具有自己的內置功能選擇方法的算法實現。
→因此,這不是任何一種特殊的特徵選擇或提取技術,它們還有助於避免過度擬合。
- 線性回歸中的套索正則化
- 在隨機森林中選擇k最佳
- 梯度提升機(GBM)
過濾器和包裝器方法之間的區別

第3部分:縮小尺寸
因此,再次從相同的問題開始,什麼是降維?
簡單來說,是將初始d維特徵空間縮小為k維特徵子空間(其中k <d)。
那麼特徵選擇和提取為什麼呢?
從某種意義上說是肯定的(但僅限於「 外行 」)。要了解這一點,我們必須更深入地研究。
在機器學習中,維數只是指數據集中特徵(即輸入變量)的數量。當特徵數量相對於數據集中的觀測數量非常多時,某些算法將難以訓練有效的模型。這稱為「維數詛咒」,它與依賴於距離計算的聚類算法特別相關。
(Quora用戶為「維數詛咒」提供了一個很好的類比,看看)
因此,當您擁有100甚至1000個特徵時,那次您只有一個選擇Dimension Reduction。讓我們討論兩種極其健壯和流行的技術。
- 線性判別分析(LDA):是的,它與Filter方法(如上所述)一起也被用作降維技術。
→當標記了功能時,我們在監督學習中使用了LDA。
→請準備並了解LDA(如果尚未安裝)。
2.主成分分析(PCA):PCA的主要目的是對數據進行分析以識別模式,並找到模式以減小數據集的維數,同時將信息損失降至最低。
→PCA將嘗試通過探索數據的一個特徵如何根據其他特徵(線性相關性)來表達來降低維數。相反,特徵選擇要考慮目標。
→PCA在具有3個或更大維度的數據集上效果最佳。因為,隨着維數的增加,從結果數據云中進行解釋變得越來越困難。
(PCA有點複雜,是的。在這裡進行解釋會使這個已經很長的博客更加無聊。因此,請使用這兩個出色的資料來理解,
ii。喬什·斯塔默(Josh Starmer)的視頻解釋(來自StatQuest的同一個人)
w ^敲擊起來:但不是由包裝方法(杜…😜)。這到系列的結尾。最後(但不是列表)提示:
一世。永遠不要忽略特徵工程或特徵選擇,並將所有內容保留在算法中。
ii。在尾注中,我分享了兩個非常有用且功能強大的工具(請記住我的話,這對您有很大幫助)




Comments