在之前的文章中,无监督学习是作为一组统计工具引入的,其中有一组特征,但没有目标。因此,本教程将与其他教程不同,因为我们无法进行预测。
相反,我们将使用k-means聚类来对图像执行颜色量化。
然后,我们将使用PCA来减少维度和数据集的可视化。
完整的笔记本电脑,请点击这里。
旋转你的Jupyter笔记本,让我们走吧!
建立
在开始任何实现之前,我们将导入一些稍后将变得方便的库:
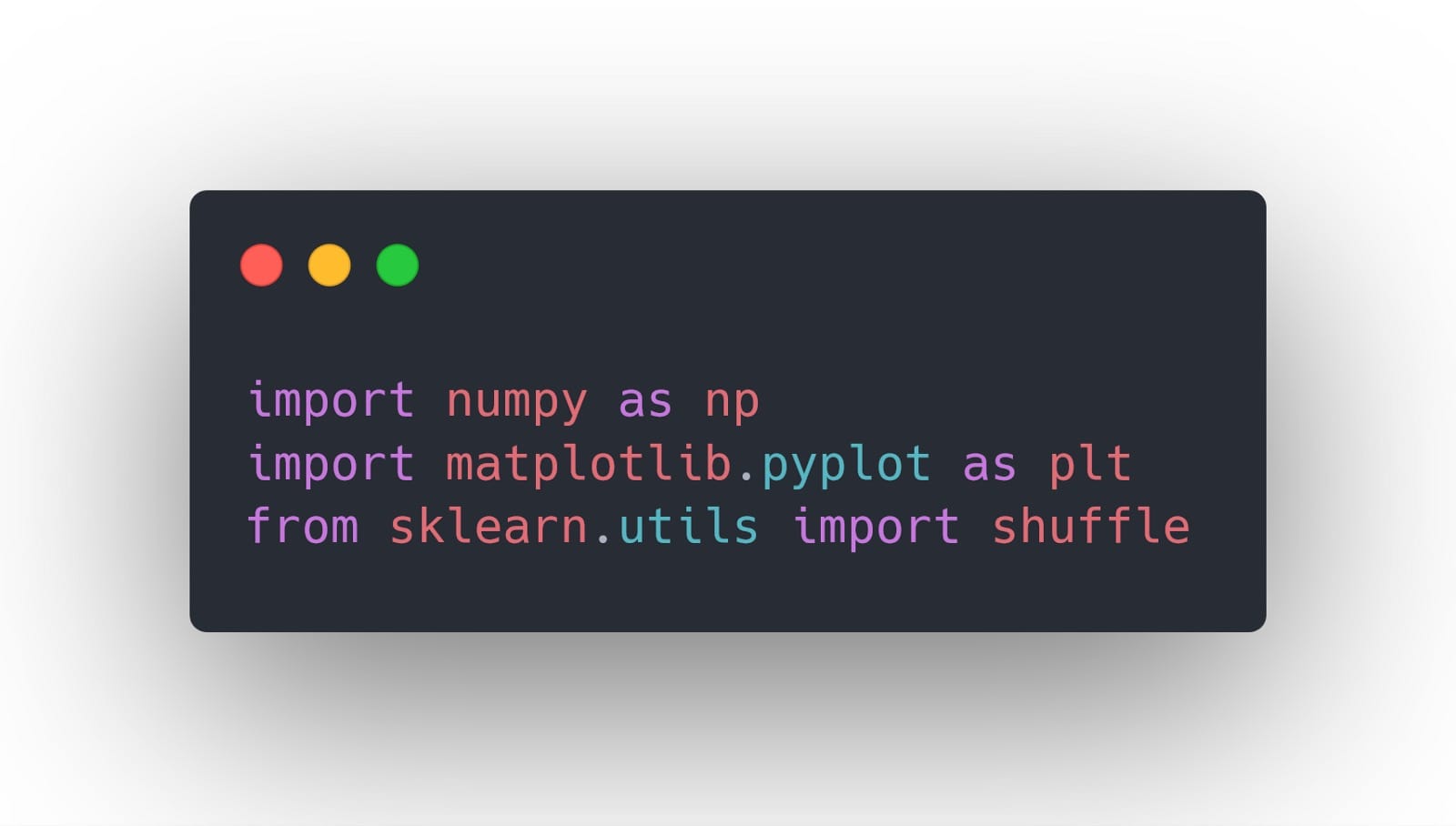
与以前的教程不同,我们不会导入数据集。相反,我们将使用scikit-learn库提供的数据。
颜色量化 – k均值聚类
很快,颜色量化是减少图像中使用的不同颜色数量的技术。这对于压缩图像同时保持图像的完整性特别有用。
首先,我们导入以下库:

请注意,我们导入了一个名为load_sample_image的示例数据集。这只包含两个图像。我们将使用其中一个来执行颜色量化。
所以,让我们展示一下我们将用于此练习的图像:

你应该看到:

现在,对于颜色量化,必须遵循不同的步骤。
首先,我们需要将图像更改为2D矩阵以进行操作:

然后,我们训练我们的模型聚合颜色,以便在图像中有64种不同的颜色:
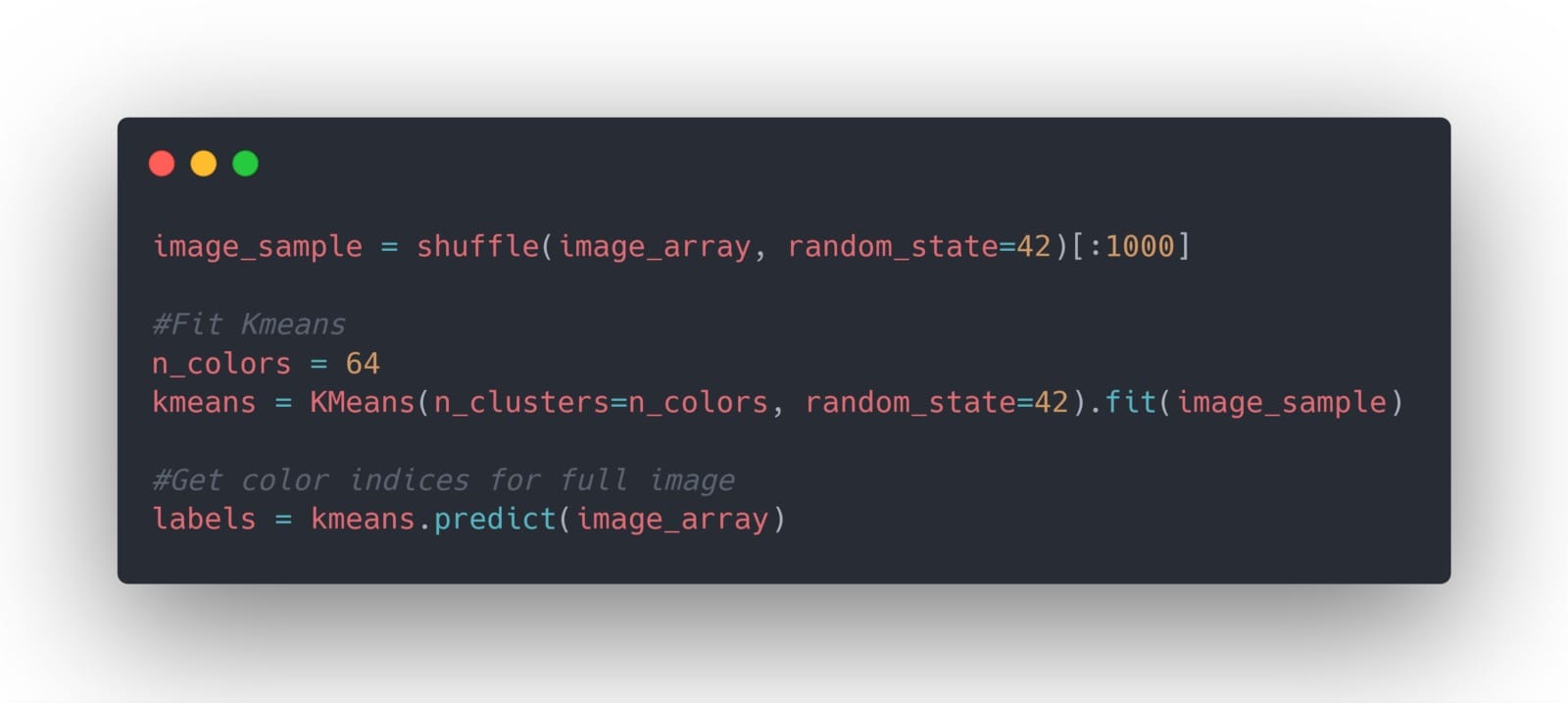
然后,我们构建一个辅助函数来帮助我们使用指定颜色的数量重建图像:
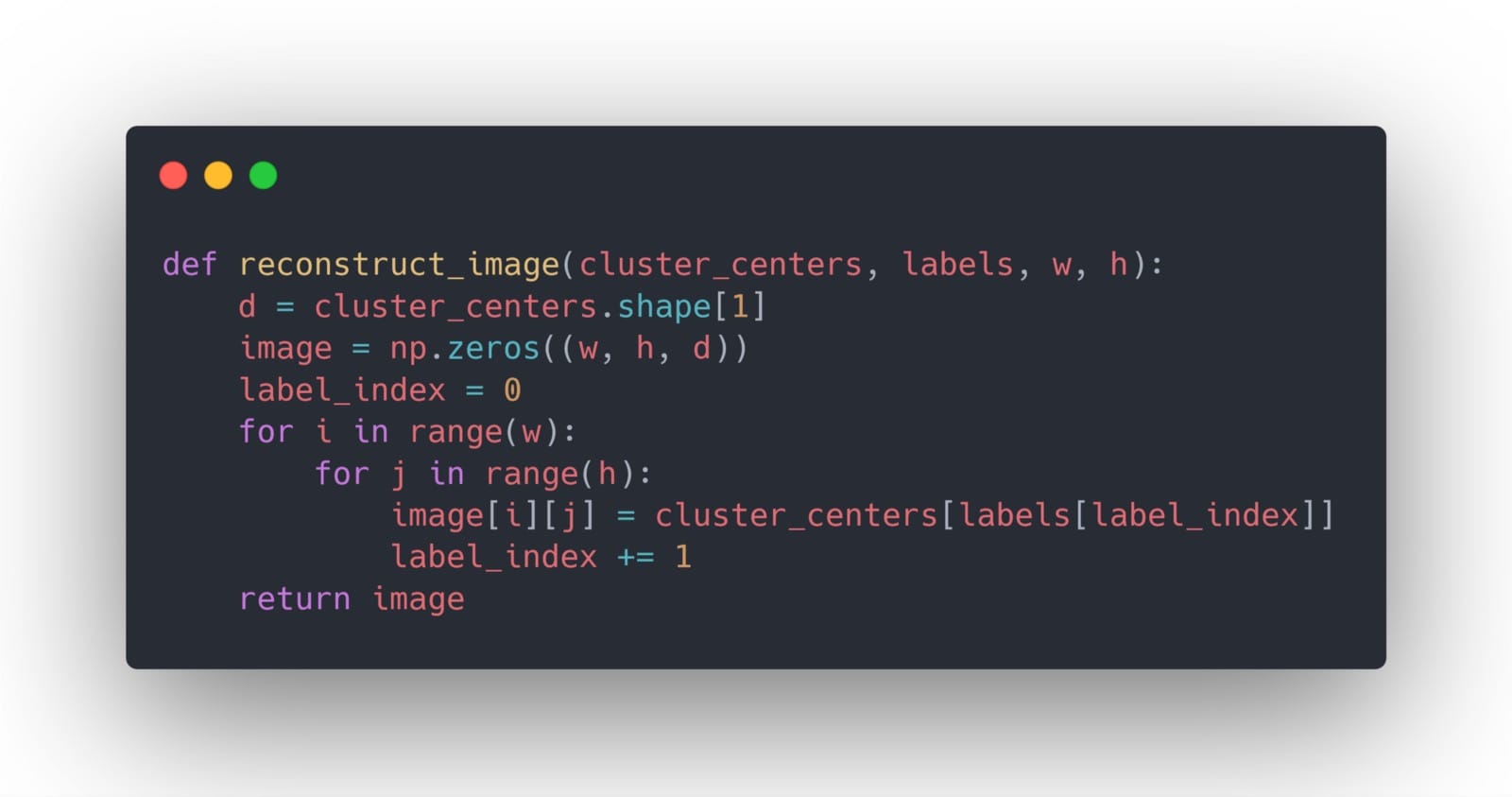
最后,我们现在可以使用64种颜色可视化图像的外观,以及它与原始图像的比较方式:


当然,我们可以看到一些差异,但总体而言,图像的完整性得到了保护!探索不同数量的集群!例如,如果指定10种颜色,可以使用以下内容:

维度降低 – PCA
在本练习中,我们将使用PCA来减少数据集的维度,以便我们可以轻松地将其可视化。
因此,让我们从scikit-learn导入虹膜数据集:

现在,我们将计算前两个主要组件,并查看每个组件可以解释的方差比例:

从上面的代码块中,您应该看到第一个主成分包含92%的方差,而第二个主成分包含5%的方差。因此,这意味着只有两个特征足以解释数据集中97%的方差!
现在,我们可以使用它来轻松地在两个维度上绘制数据:
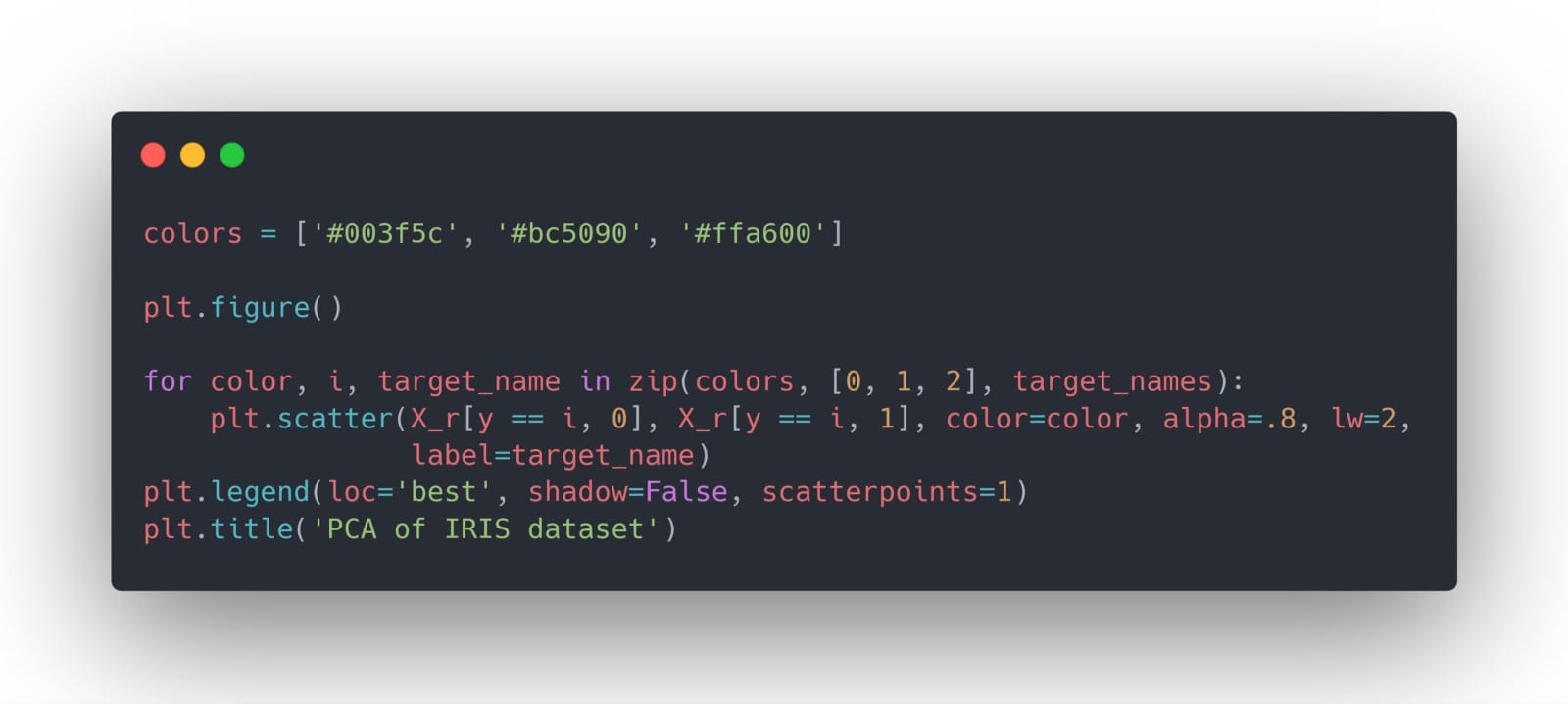
你得到:
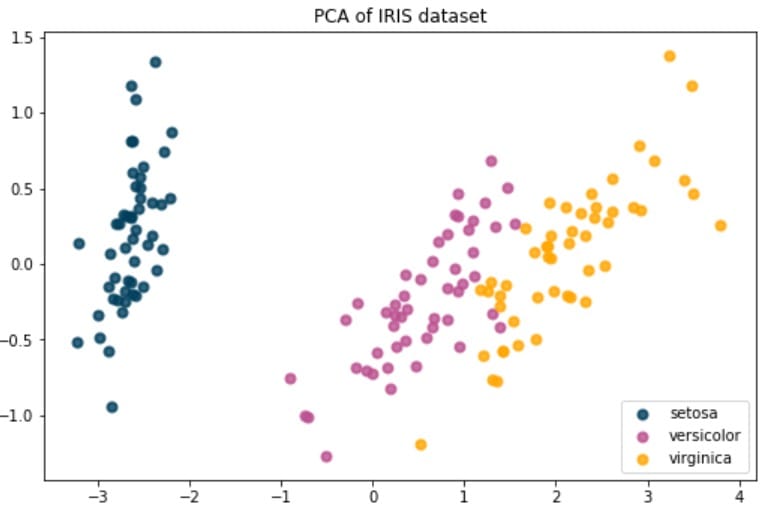
而已!您现在知道如何实现k-means和PCA!同样,请记住,无监督学习很难,因为没有误差指标来评估算法的执行情况。而且,这些技术通常在进行监督学习之前用于探索性数据分析。
本文转自towardsdatascience,原文地址



Comments