Author Archive

循環神經網絡 – Recurrent Neural Network | RNN

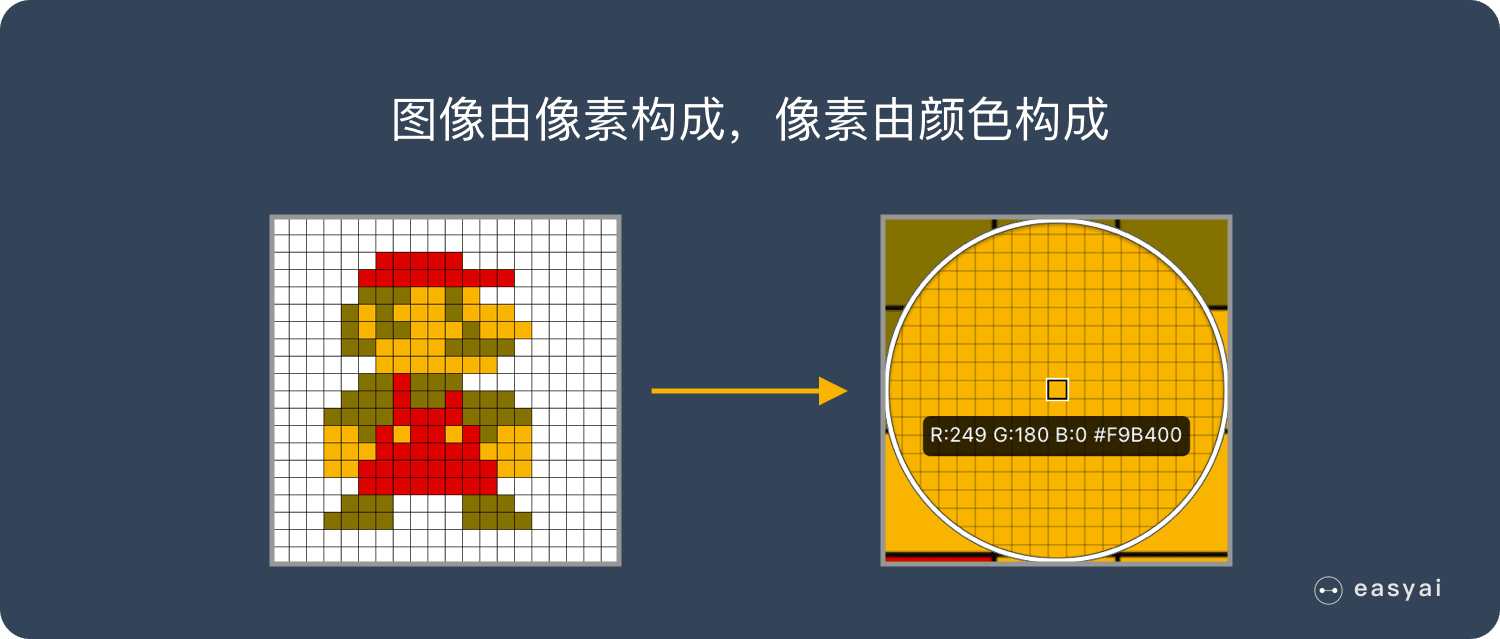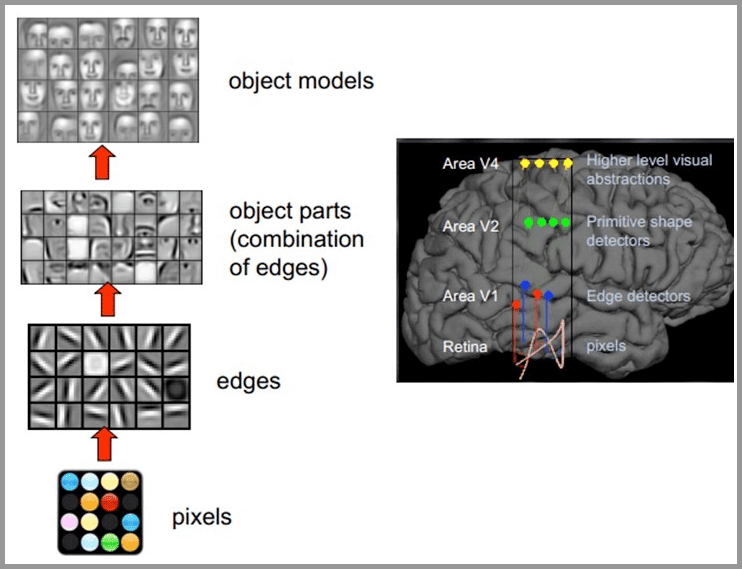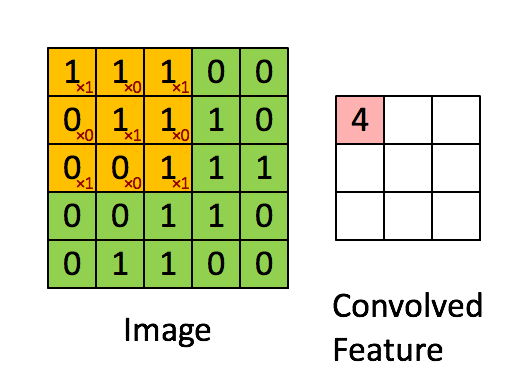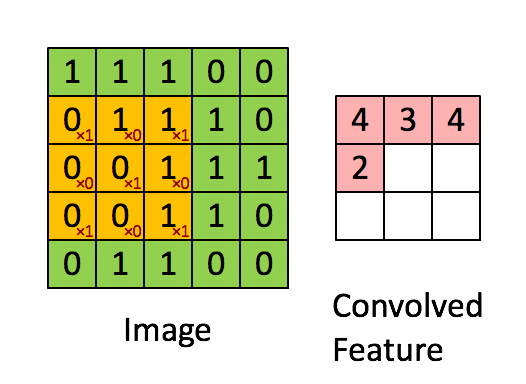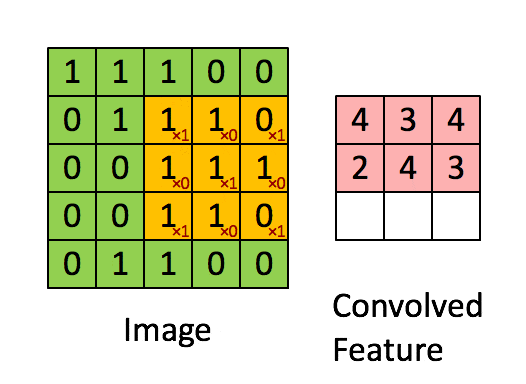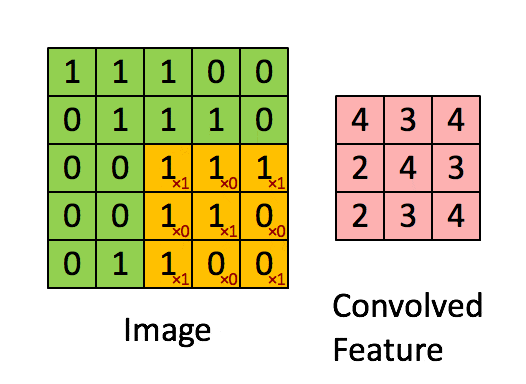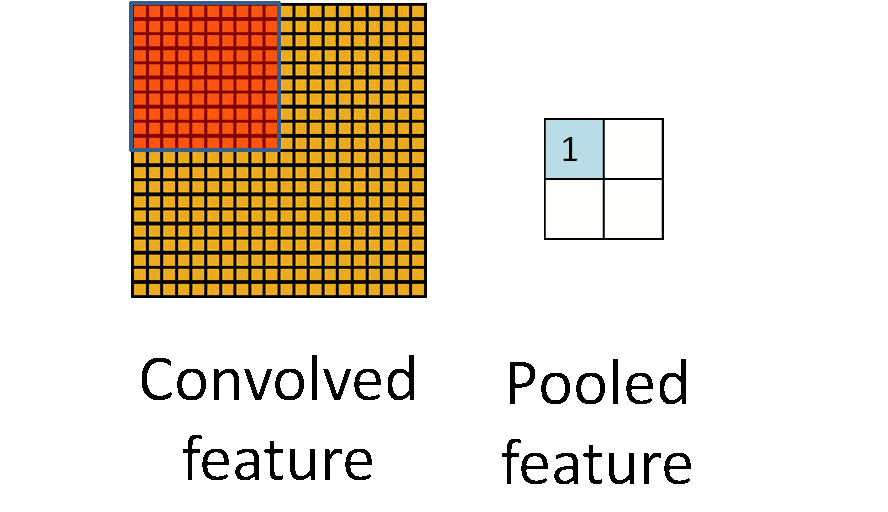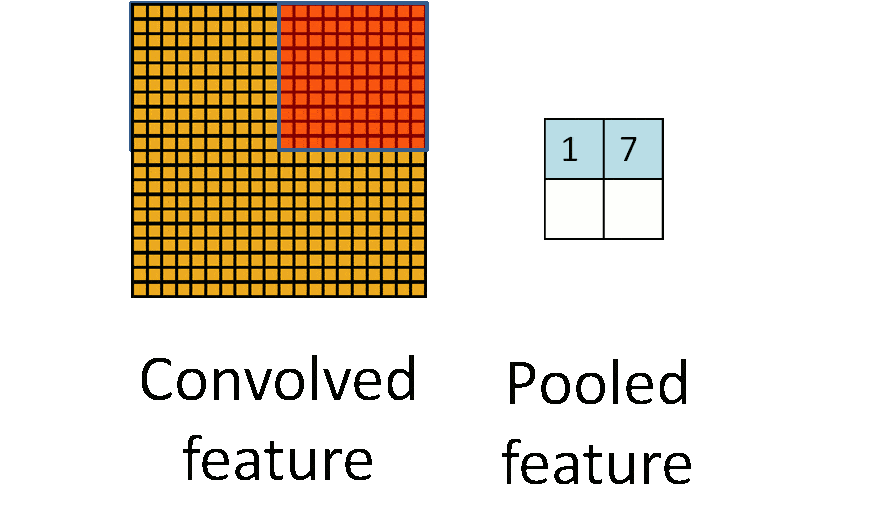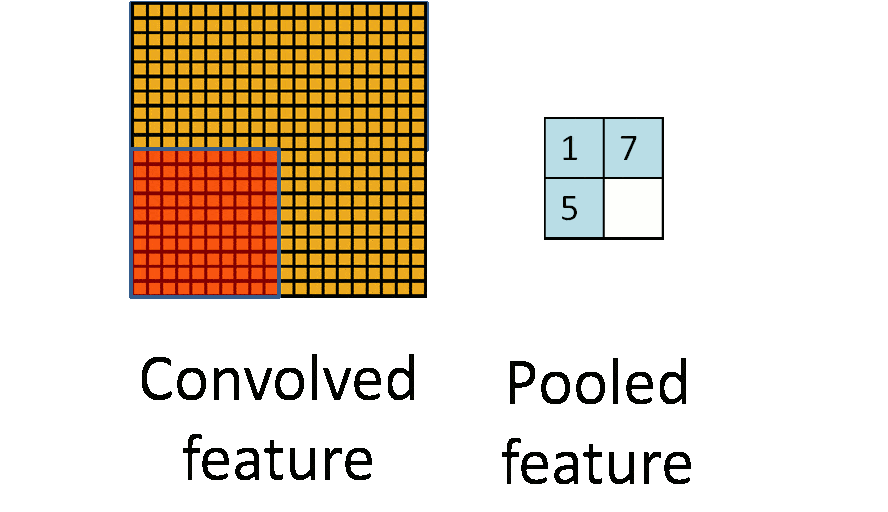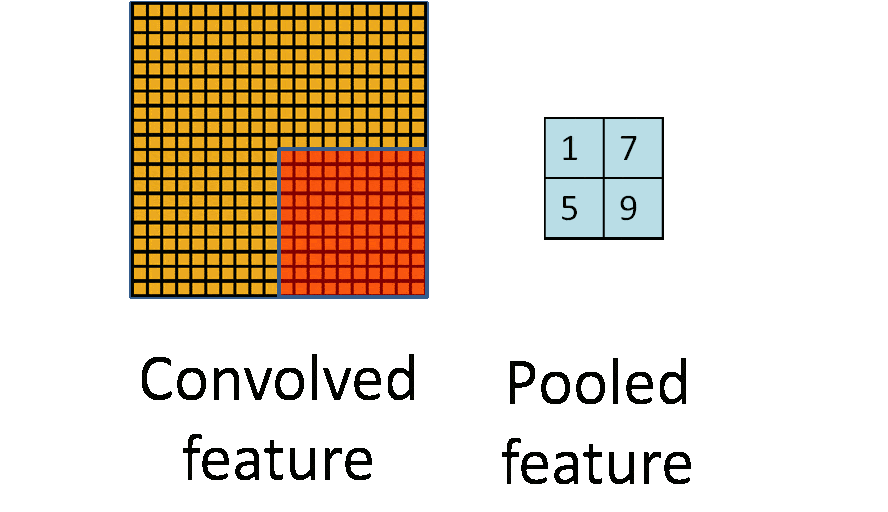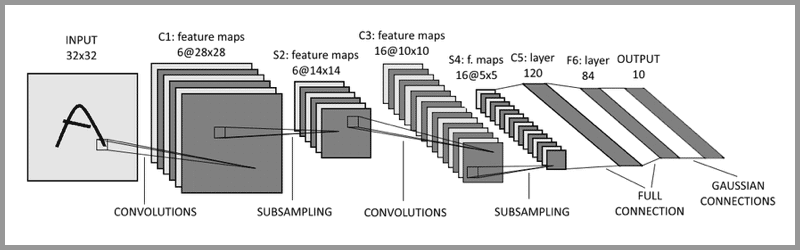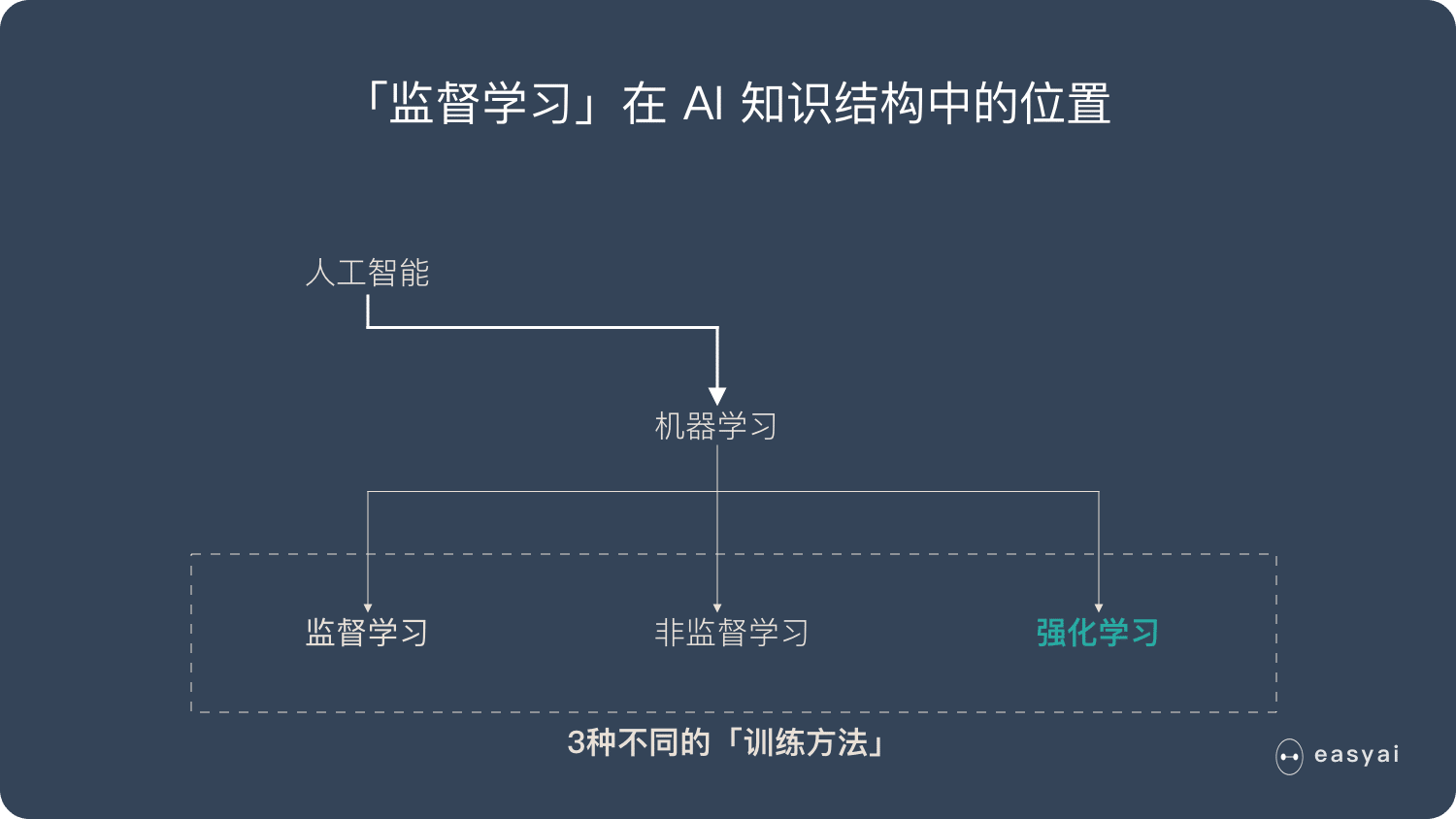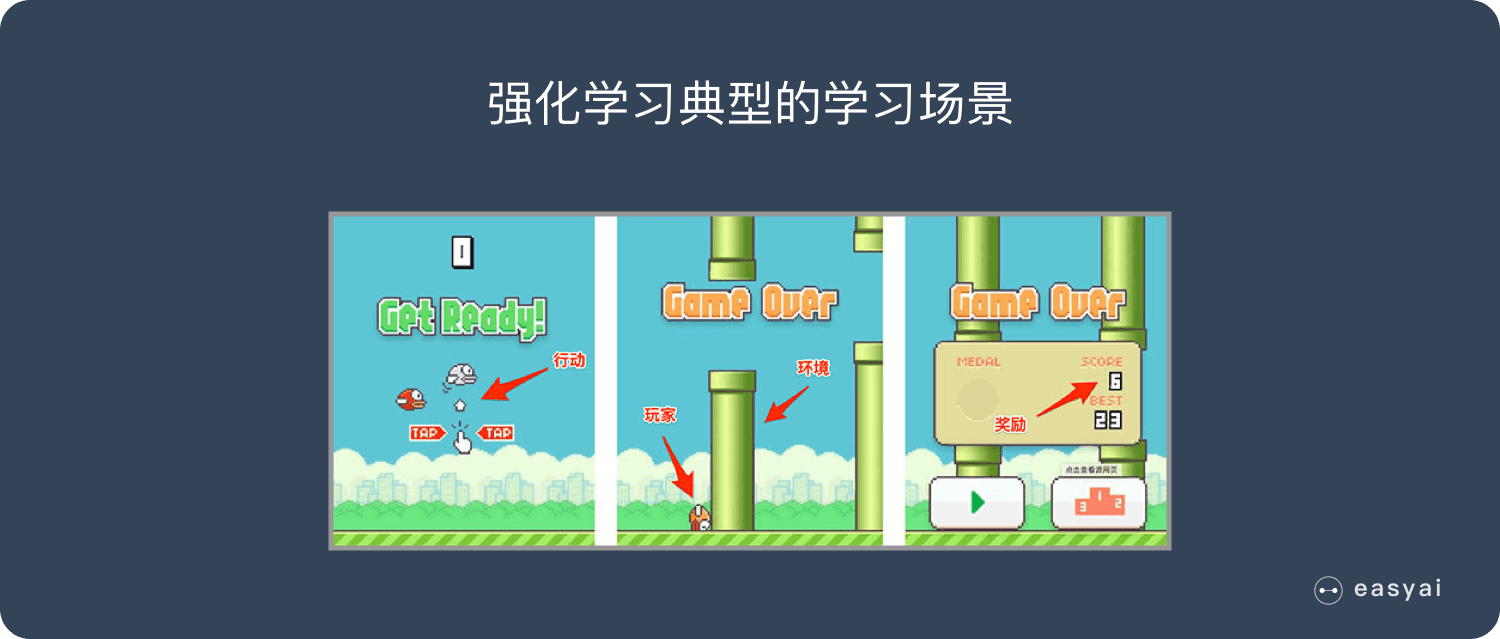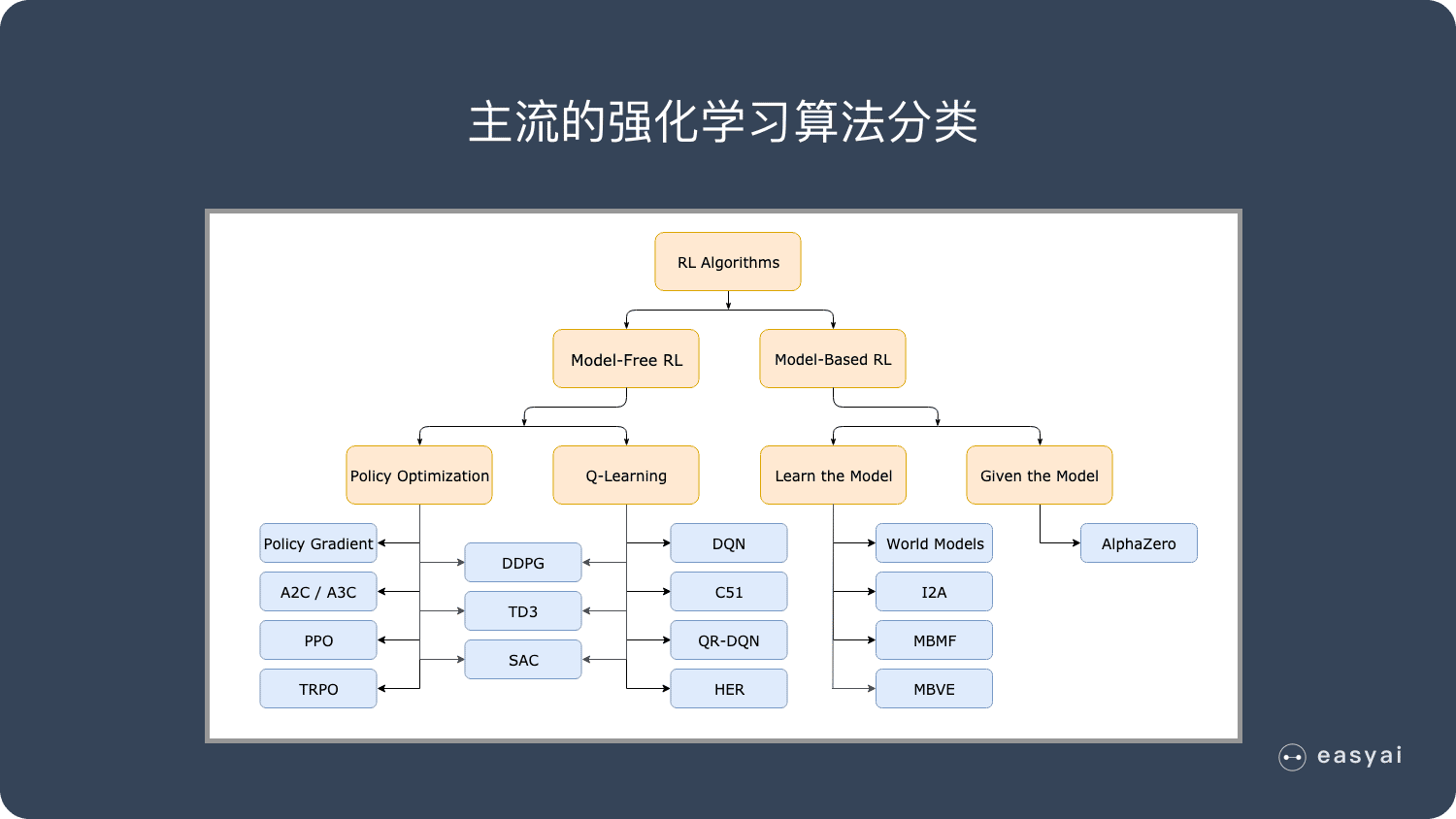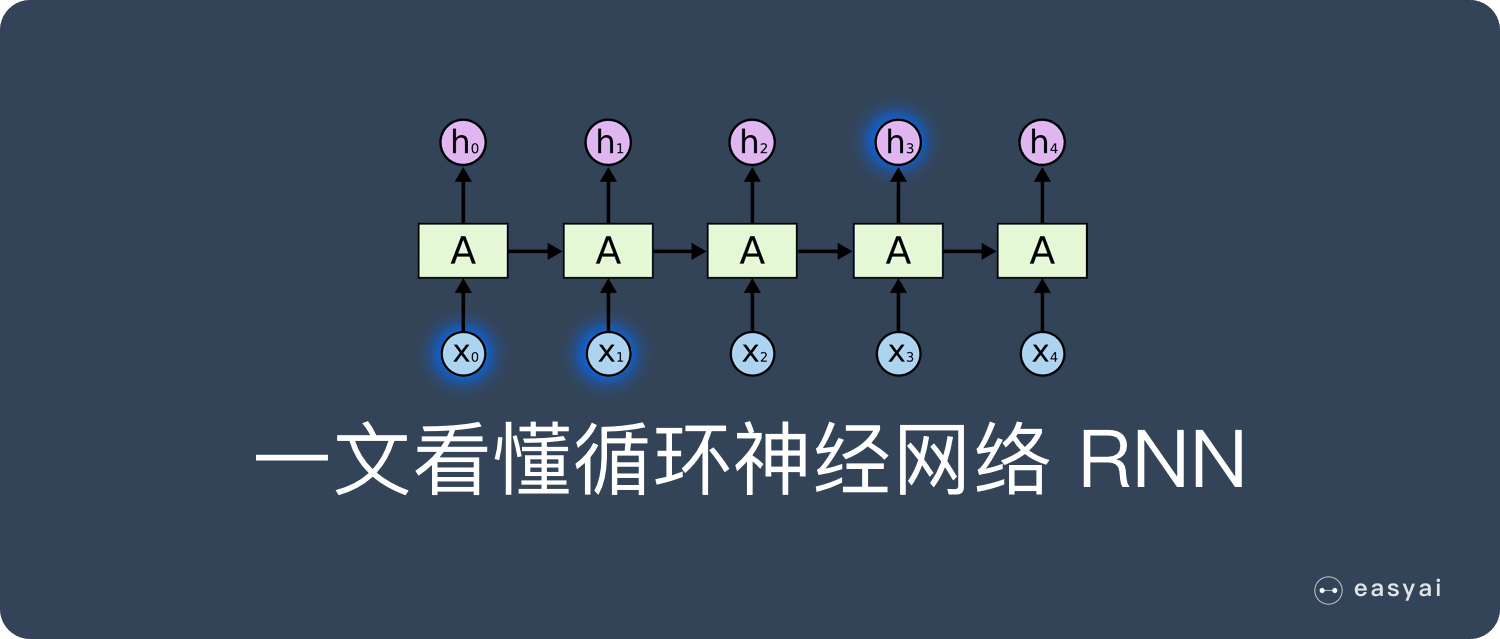
一文看懂循環神經網絡RNN

卷積神經網絡 – CNN 已經很強大的，為什麼還需要RNN？

本文會用通俗易懂的方式來解釋 RNN 的獨特價值——處理序列數據。同時還會說明 RNN 的一些缺陷和它的變種算法。

最後給大家介紹一下 RNN 的實際應用價值和使用場景。

 

為什麼需要 RNN ？獨特價值是什麼？

卷積神經網絡 – CNN 和普通的算法大部分都是輸入和輸出的一一對應，也就是一個輸入得到一個輸出。不同的輸入之間是沒有聯繫的。

大部分算法都是輸入和輸出的一一對應

但是在某些場景中，一個輸入就不夠了！

為了填好下面的空，取前面任何一個詞都不合適，我們不但需要知道前面所有的詞，還需要知道詞之間的順序。

序列數據的處理

這種需要處理「序列數據 – 一串相互依賴的數據流」的場景就需要使用 RNN 來解決了。

典型的集中序列數據：

  1. 文章里的文字內容
  2. 語音里的音頻內容
  3. 股票市場中的價格走勢
  4. ……

RNN 之所以能夠有效的處理序列數據，主要是基於他的比較特殊的運行原理。下面給大家介紹一下 RNN 的基本運行原理。

 

RNN 的基本原理

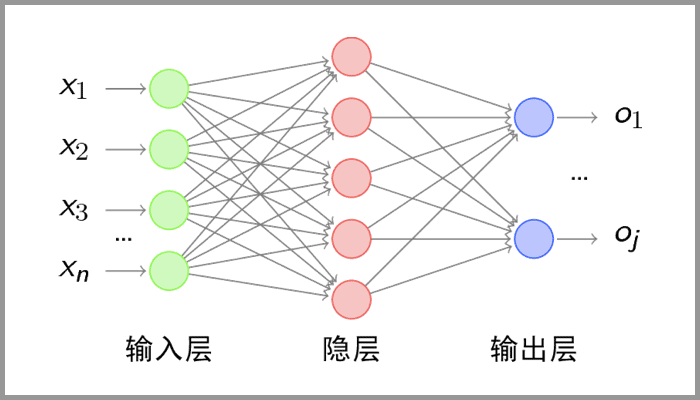
傳統神經網絡的結構比較簡單：輸入層 – 隱藏層 – 輸出層。如下圖所示：

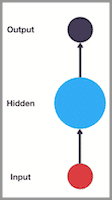
傳統神經網絡

RNN 跟傳統神經網絡最大的區別在於每次都會將前一次的輸出結果，帶到下一次的隱藏層中，一起訓練。如下圖所示：

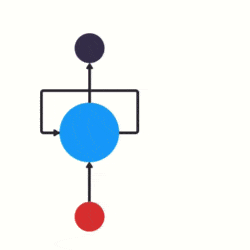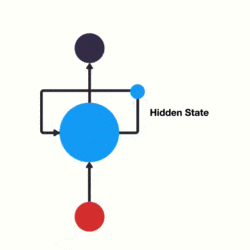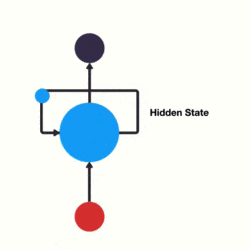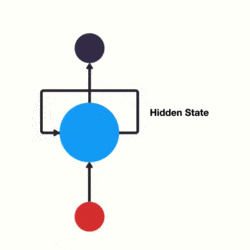
RNN區別

下面用一個具體的案例來看看 RNN 是如何工作的：

假如需要判斷用戶的說話意圖（問天氣、問時間、設置鬧鐘…），用戶說了一句「what time is it？」我們需要先對這句話進行分詞：

對輸入進行分詞

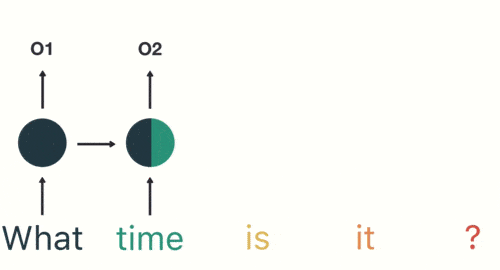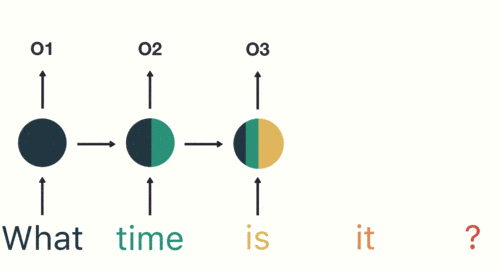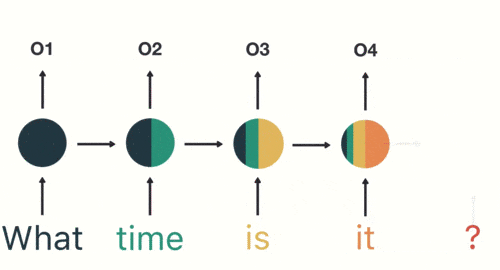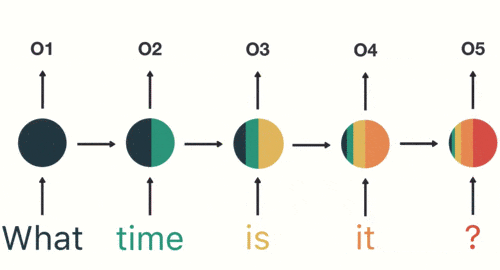
然後按照順序輸入 RNN ，我們先將 「what」作為 RNN 的輸入，得到輸出「01」

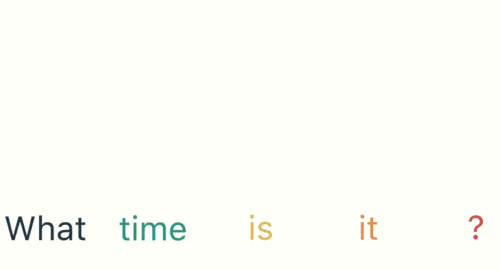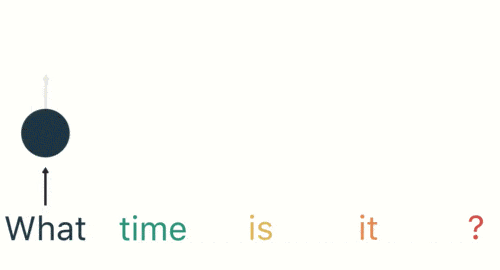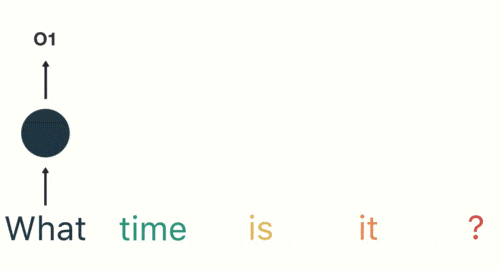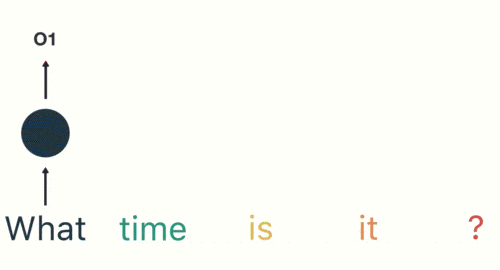
輸入what，得到輸出01

然後，我們按照順序，將「time」輸入到 RNN 網絡，得到輸出「02」。

這個過程我們可以看到，輸入 「time」 的時候，前面 「what」 的輸出也產生了影響（隱藏層中有一半是黑色的）。

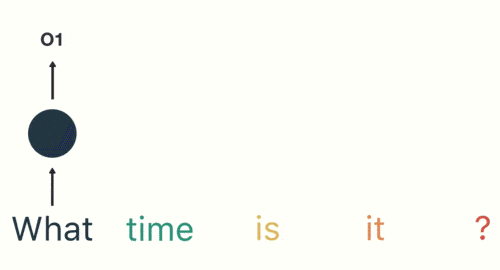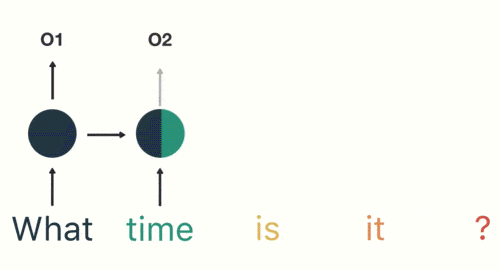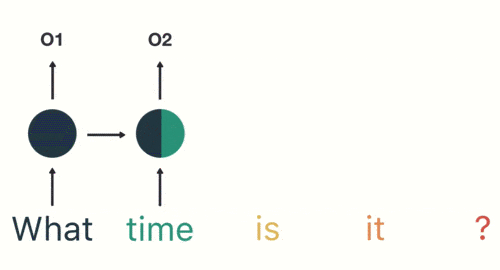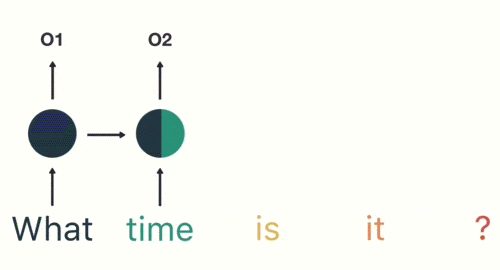
以此類推，前面所有的輸入都對未來的輸出產生了影響，大家可以看到圓形隱藏層中包含了前面所有的顏色。如下圖所示：

RNN 對前面輸入有「記憶」作用的體現

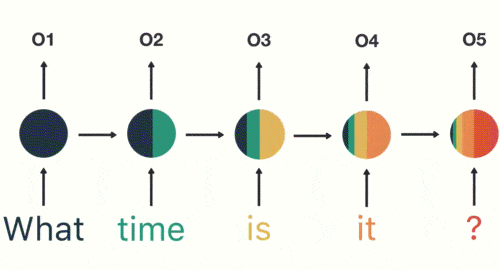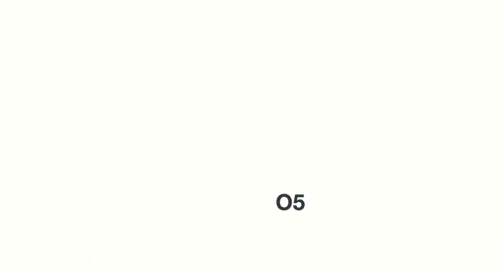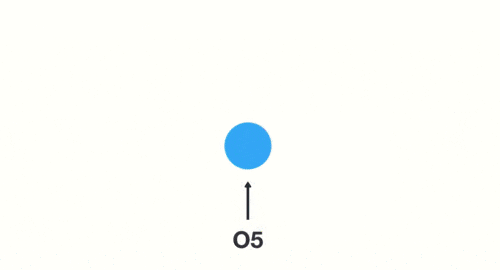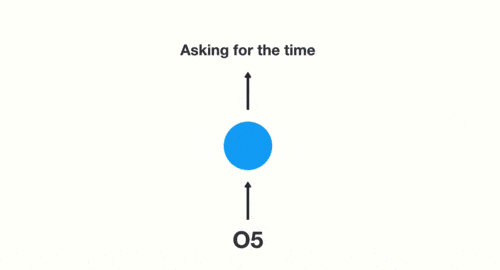
當我們判斷意圖的時候，只需要最後一層的輸出「05」，如下圖所示：

RNN 最後一層的輸出是我們最終想要的

RNN 的缺點也比較明顯

隱藏層中的顏色分佈

通過上面的例子，我們已經發現，短期的記憶影響較大（如橙色區域），但是長期的記憶影響就很小（如黑色和綠色區域），這就是 RNN 存在的短期記憶問題。

  1. RNN 有短期記憶問題，無法處理很長的輸入序列
  2. 訓練 RNN 需要投入極大的成本

由於 RNN 的短期記憶問題，後來又出現了基於 RNN 的優化算法，下面給大家簡單介紹一下。

 

RNN 的優化算法

RNN 到 LSTM – 長短期記憶網絡

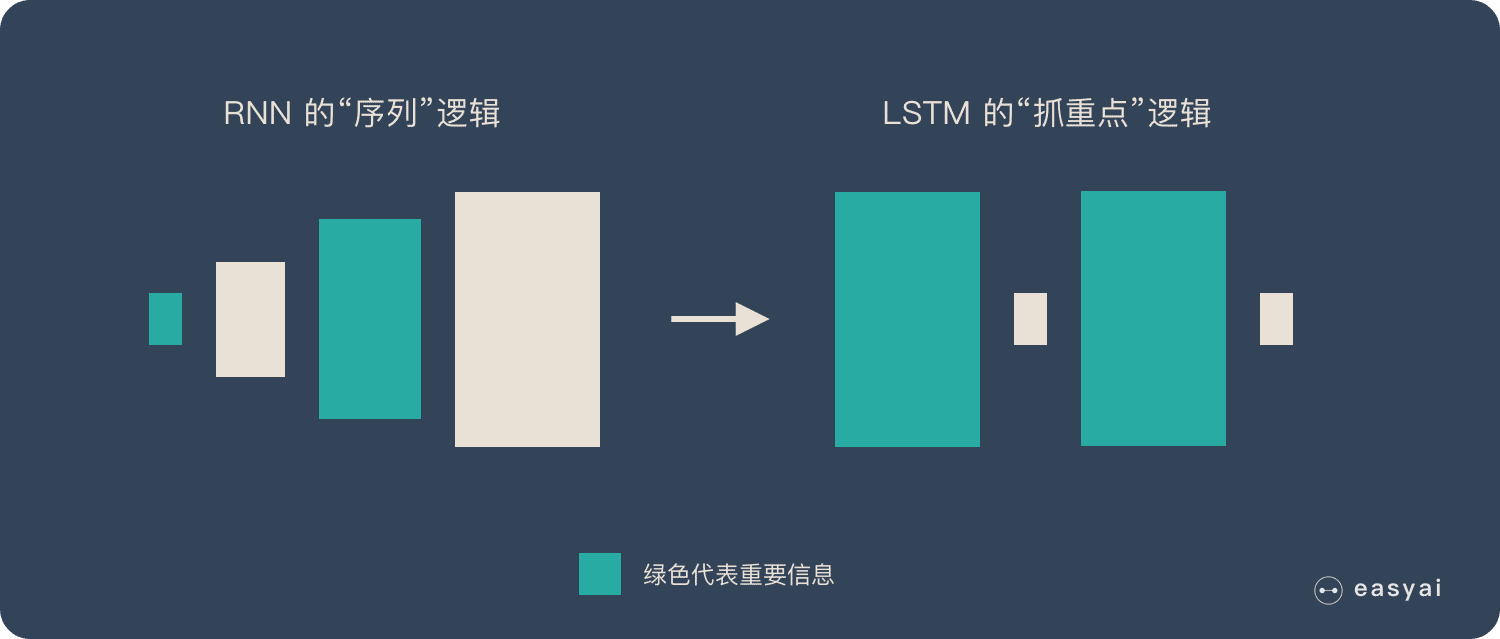
RNN 是一種死板的邏輯，越晚的輸入影響越大，越早的輸入影響越小，且無法改變這個邏輯。

LSTM 做的最大的改變就是打破了這個死板的邏輯，而改用了一套靈活了邏輯——只保留重要的信息。

簡單說就是：抓重點！

RNN的序列邏輯到LSTM的抓重點邏輯

舉個例子，我們先快速的閱讀下面這段話：

快速閱讀這段話

當我們快速閱讀完之後，可能只會記住下面幾個重點：

劃重點

LSTM 類似上面的劃重點，他可以保留較長序列數據中的「重要信息」，忽略不重要的信息。這樣就解決了 RNN 短期記憶的問題。

具體技術上的實現原理就不在這裡展開了，感興趣的可以看看 LSTM 的詳細介紹《長短期記憶網絡 – LSTM》

 

從 LSTM 到 GRU

Gated Recurrent Unit – GRU 是 LSTM 的一個變體。他保留了 LSTM 劃重點，遺忘不重要信息的特點，在long-term 傳播的時候也不會被丟失。

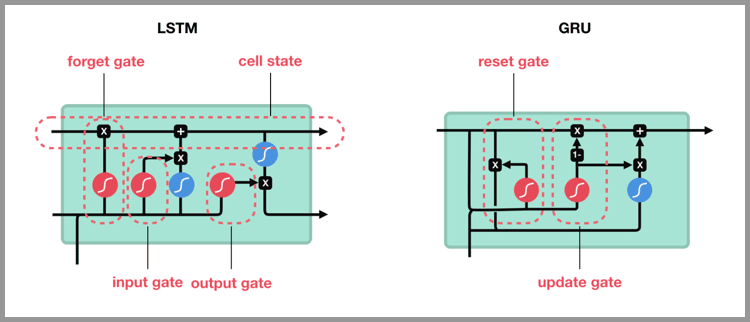
GRU 主要是在LSTM的模型上做了一些簡化和調整

GRU 主要是在 LSTM 的模型上做了一些簡化和調整，在訓練數據集比較大的情況下可以節省很多時間。

 

RNN 的應用和使用場景

只要涉及到序列數據的處理問題，都可以使用到，NLP 就是一個典型的應用場景。

RNN的應用和使用場景

文本生成：類似上面的填空題，給出前後文，然後預測空格中的詞是什麼。

機器翻譯：翻譯工作也是典型的序列問題，詞的順序直接影響了翻譯的結果。

語音識別：根據輸入音頻判斷對應的文字是什麼。

生成圖像描述：類似看圖說話，給一張圖，能夠描述出圖片中的內容。這個往往是 RNN 和 CNN 的結合。

生成圖像描述

視頻標記：他將視頻分解為圖片，然後用圖像描述來描述圖片內容。

 

總結

RNN的獨特價值在於：它能有效的處理序列數據。比如：文章內容、語音音頻、股票價格走勢…

之所以他能處理序列數據，是因為在序列中前面的輸入也會影響到後面的輸出，相當於有了「記憶功能」。但是 RNN 存在嚴重的短期記憶問題，長期的數據影響很小（哪怕他是重要的信息）。

於是基於 RNN 出現了 LSTM 和 GRU 等變種算法。這些變種算法主要有幾個特點：

  1. 長期信息可以有效的保留
  2. 挑選重要信息保留，不重要的信息會選擇「遺忘」

RNN 幾個典型的應用如下：

  1. 文本生成
  2. 語音識別
  3. 機器翻譯
  4. 生成圖像描述
  5. 視頻標記

 

百度百科+維基百科

百度百科版本

循環神經網絡（Recurrent Neural Network, RNN）是一類以序列（sequence）數據為輸入，在序列的演進方向進行遞歸（recursion）且所有節點（循環單元）按鏈式連接形成閉合迴路的遞歸神經網絡（recursive neural network）。

對循環神經網絡的研究始於二十世紀80-90年代，並在二十一世紀初發展為重要的深度學習（deep learning）算法 ，其中雙向循環神經網絡（Bidirectional RNN, Bi-RNN）和長短期記憶網絡（Long Short-Term Memory networks，LSTM）是常見的的循環神經網絡。

循環神經網絡具有記憶性、參數共享並且圖靈完備（Turing completeness），因此能以很高的效率對序列的非線性特徵進行學習。循環神經網絡在自然語言處理（Natural Language Processing, NLP），例如語音識別、語言建模、機器翻譯等領域有重要應用，也被用於各類時間序列預報或與卷積神經網絡（Convoutional Neural Network,CNN）相結合處理計算機視覺問題。

查看詳情

維基百科版本

循環神經網絡（RNN）是一類神經網絡，其中節點之間的連接形成一個有向圖沿着序列。這允許它展示時間序列的時間動態行為。與前饋神經網絡不同，RNN可以使用其內部狀態（存儲器）來處理輸入序列。這使它們適用於諸如未分段，連接手寫識別或語音識別等任務。

術語「遞歸神經網絡」被不加選擇地用於指代具有類似一般結構的兩大類網絡，其中一個是有限脈衝而另一個是無限脈衝。兩類網絡都表現出時間動態行為。有限脈衝遞歸網絡是一種有向無環圖，可以展開並用嚴格的前饋神經網絡代替，而無限脈衝循環網絡是一種無法展開的有向循環圖。

有限脈衝和無限脈衝周期性網絡都可以具有額外的存儲狀態，並且存儲可以由神經網絡直接控制。如果存儲包含時間延遲或具有反饋循環，則存儲也可以由另一個網絡或圖表替換。這種受控狀態稱為門控狀態或門控存儲器，並且是長短期存儲器網絡（LSTM）和門控循環單元的一部分。

查看詳情

 

入門類文章（2）

如何理解RNN？（理論篇）

2種簡單的方式緩解RNN的優化問題

實踐類文章（1）

ACL 2018｜西北大學：RNN語言模型的重要訓練數據抽樣

卷積神經網絡 – CNN

一文看懂卷積神經網絡-CNN

卷積神經網絡 – CNN 最擅長的就是圖片的處理。它受到人類視覺神經系統的啟發。

CNN 有2大特點：

  1. 能夠有效的將大數據量的圖片降維成小數據量
  2. 能夠有效的保留圖片特徵，符合圖片處理的原則

目前 CNN 已經得到了廣泛的應用，比如：人臉識別、自動駕駛、美圖秀秀、安防等很多領域。

 

CNN 解決了什麼問題？

在 CNN 出現之前，圖像對於人工智能來說是一個難題，有2個原因：

  1. 圖像需要處理的數據量太大，導致成本很高，效率很低
  2. 圖像在數字化的過程中很難保留原有的特徵，導致圖像處理的準確率不高

下面就詳細說明一下這2個問題：

 

需要處理的數據量太大

圖像是由像素構成的，每個像素又是由顏色構成的。

圖像是由像素構成的，每個像素又是由顏色構成的

現在隨隨便便一張圖片都是 1000×1000 像素以上的， 每個像素都有RGB 3個參數來表示顏色信息。

假如我們處理一張 1000×1000 像素的圖片，我們就需要處理3百萬個參數！

1000×1000×3=3,000,000

這麼大量的數據處理起來是非常消耗資源的，而且這只是一張不算太大的圖片！

卷積神經網絡 – CNN 解決的第一個問題就是「將複雜問題簡化」，把大量參數降維成少量參數，再做處理。

更重要的是：我們在大部分場景下，降維並不會影響結果。比如1000像素的圖片縮小成200像素，並不影響肉眼認出來圖片中是一隻貓還是一隻狗，機器也是如此。

 

保留圖像特徵

圖片數字化的傳統方式我們簡化一下，就類似下圖的過程：

圖像簡單數字化無法保留圖像特徵

假如有圓形是1，沒有圓形是0，那麼圓形的位置不同就會產生完全不同的數據表達。但是從視覺的角度來看，圖像的內容（本質）並沒有發生變化，只是位置發生了變化。

所以當我們移動圖像中的物體，用傳統的方式的得出來的參數會差異很大！這是不符合圖像處理的要求的。

而 CNN 解決了這個問題，他用類似視覺的方式保留了圖像的特徵，當圖像做翻轉，旋轉或者變換位置時，它也能有效的識別出來是類似的圖像。

那麼卷積神經網絡是如何實現的呢？在我們了解 CNN 原理之前，先來看看人類的視覺原理是什麼？

 

人類的視覺原理

深度學習的許多研究成果，離不開對大腦認知原理的研究，尤其是視覺原理的研究。

1981 年的諾貝爾醫學獎，頒發給了 David Hubel（出生於加拿大的美國神經生物學家） 和TorstenWiesel，以及 Roger Sperry。前兩位的主要貢獻，是「發現了視覺系統的信息處理」，可視皮層是分級的。

人類的視覺原理如下：從原始信號攝入開始（瞳孔攝入像素 Pixels），接着做初步處理（大腦皮層某些細胞發現邊緣和方向），然後抽象（大腦判定，眼前的物體的形狀，是圓形的），然後進一步抽象（大腦進一步判定該物體是只氣球）。下面是人腦進行人臉識別的一個示例：

人類視覺原理1

 

對於不同的物體，人類視覺也是通過這樣逐層分級，來進行認知的：

人類視覺原理2

我們可以看到，在最底層特徵基本上是類似的，就是各種邊緣，越往上，越能提取出此類物體的一些特徵（輪子、眼睛、軀幹等），到最上層，不同的高級特徵最終組合成相應的圖像，從而能夠讓人類準確的區分不同的物體。

那麼我們可以很自然的想到：可以不可以模仿人類大腦的這個特點，構造多層的神經網絡，較低層的識別初級的圖像特徵，若干底層特徵組成更上一層特徵，最終通過多個層級的組合，最終在頂層做出分類呢？

答案是肯定的，這也是許多深度學習算法（包括CNN）的靈感來源。

 

卷積神經網絡-CNN 的基本原理

典型的 CNN 由3個部分構成：

  1. 卷積層
  2. 池化層
  3. 全連接層

如果簡單來描述的話：

卷積層負責提取圖像中的局部特徵；池化層用來大幅降低參數量級(降維)；全連接層類似傳統神經網絡的部分，用來輸出想要的結果。

典型的 CNN 由3個部分構成

下面的原理解釋為了通俗易懂，忽略了很多技術細節，如果大家對詳細的原理感興趣，可以看這個視頻《卷積神經網絡基礎》。

 

卷積——提取特徵

卷積層的運算過程如下圖，用一個卷積核掃完整張圖片：

卷積層運算過程

這個過程我們可以理解為我們使用一個過濾器（卷積核）來過濾圖像的各個小區域，從而得到這些小區域的特徵值。

在具體應用中，往往有多個卷積核，可以認為，每個卷積核代表了一種圖像模式，如果某個圖像塊與此卷積核卷積出的值大，則認為此圖像塊十分接近於此卷積核。如果我們設計了6個卷積核，可以理解：我們認為這個圖像上有6種底層紋理模式，也就是我們用6中基礎模式就能描繪出一副圖像。以下就是25種不同的卷積核的示例：

25種不同的卷積核

總結：卷積層的通過卷積核的過濾提取出圖片中局部的特徵，跟上面提到的人類視覺的特徵提取類似。

 

池化層（下採樣）——數據降維，避免過擬合

池化層簡單說就是下採樣，他可以大大降低數據的維度。其過程如下：

池化層過程

上圖中，我們可以看到，原始圖片是20×20的，我們對其進行下採樣，採樣窗口為10×10，最終將其下採樣成為一個2×2大小的特徵圖。

之所以這麼做的原因，是因為即使做完了卷積，圖像仍然很大（因為卷積核比較小），所以為了降低數據維度，就進行下採樣。

總結：池化層相比卷積層可以更有效的降低數據維度，這麼做不但可以大大減少運算量，還可以有效的避免過擬合。

 

全連接層——輸出結果

這個部分就是最後一步了，經過卷積層和池化層處理過的數據輸入到全連接層，得到最終想要的結果。

經過卷積層和池化層降維過的數據，全連接層才能”跑得動”，不然數據量太大，計算成本高，效率低下。

全連接層

典型的 CNN 並非只是上面提到的3層結構，而是多層結構，例如 LeNet-5 的結構就如下圖所示：

卷積層 – 池化層- 卷積層 – 池化層 – 卷積層 – 全連接層

LeNet-5網絡結構

在了解了 CNN 的基本原理後，我們重點說一下 CNN 的實際應用有哪些。

 

CNN 有哪些實際應用？

卷積神經網絡 – CNN 很擅長處理圖像。而視頻是圖像的疊加，所以同樣擅長處理視頻內容。下面給大家列一些比較成熟的應用：

 

圖像分類、檢索

圖像分類是比較基礎的應用，他可以節省大量的人工成本，將圖像進行有效的分類。對於一些特定領域的圖片，分類的準確率可以達到 95%+，已經算是一個可用性很高的應用了。

典型場景：圖像搜索…

CNN應用-圖像分類、檢索

 

目標定位檢測

可以在圖像中定位目標，並確定目標的位置及大小。

典型場景：自動駕駛、安防、醫療…

CNN應用-目標

 

目標分割

簡單理解就是一個像素級的分類。

他可以對前景和背景進行像素級的區分、再高級一點還可以識別出目標並且對目標進行分類。

典型場景：美圖秀秀、視頻後期加工、圖像生成…

CNN應用-目標分割

 

人臉識別

人臉識別已經是一個非常普及的應用了，在很多領域都有廣泛的應用。

典型場景：安防、金融、生活…

CNN應用-人臉識別

 

骨骼識別

骨骼識別是可以識別身體的關鍵骨骼，以及追蹤骨骼的動作。

典型場景：安防、電影、圖像視頻生成、遊戲…

CNN應用-骨骼識別

 

總結

今天我們介紹了 CNN 的價值、基本原理和應用場景，簡單總結如下：

CNN 的價值：

  1. 能夠將大數據量的圖片有效的降維成小數據量(並不影響結果)
  2. 能夠保留圖片的特徵，類似人類的視覺原理

CNN 的基本原理：

  1. 卷積層 – 主要作用是保留圖片的特徵
  2. 池化層 – 主要作用是把數據降維，可以有效的避免過擬合
  3. 全連接層 – 根據不同任務輸出我們想要的結果

CNN 的實際應用：

  1. 圖片分類、檢索
  2. 目標定位檢測
  3. 目標分割
  4. 人臉識別
  5. 骨骼識別

 

百度百科+維基百科

百度百科版本

卷積神經網絡（Convolutional Neural Networks, CNN）是一類包含卷積計算且具有深度結構的前饋神經網絡（Feedforward Neural Networks），是深度學習（deep learning）的代表算法之一 。由於卷積神經網絡能夠進行平移不變分類（shift-invariant classification），因此也被稱為「平移不變人工神經網絡（Shift-Invariant Artificial Neural Networks, SIANN）」 。

對卷積神經網絡的研究始於二十世紀80至90年代，時間延遲網絡和LeNet-5是最早出現的卷積神經網絡；在二十一世紀後，隨着深度學習理論的提出和數值計算設備的改進，卷積神經網絡得到了快速發展，並被大量應用於計算機視覺、自然語言處理等領域 。

查看詳情

維基百科版本

在深度學習中，卷積神經網絡（CNN或ConvNet）是一類深度神經網絡，最常用於分析視覺圖像。

CNN使用多層感知器的變體設計，需要最少的預處理。它們也被稱為移位不變或空間不變人工神經網絡（SIANN），基於它們的共享權重架構和平移不變性特徵。卷積網絡被啟發由生物工藝在之間的連接圖案的神經元類似於動物的組織視覺皮層。個體皮層神經元僅在被稱為感受野的視野的受限區域中對刺激作出反應。不同神經元的感受野部分重疊，使得它們覆蓋整個視野。

與其他圖像分類算法相比，CNN使用相對較少的預處理。這意味着網絡學習傳統算法中手工設計的過濾器。這種與特徵設計中的先前知識和人力的獨立性是一個主要優點。

它們可用於圖像和視頻識別，推薦系統，圖像分類，醫學圖像分析和自然語言處理。

查看詳情

 

開拓視野類文章（11）

乾貨|卷積有多少種？一文讀懂深度學習中的各種卷積（2019-10）

卷積神經網絡中十大拍案叫絕的操作（2019-9）

「多圖」圖解10大CNN架構（2019-7）

總結12大CNN主流模型架構設計思想（2019-6）

卷積神經網絡中十大拍案叫絕的操作（2019-5）

CNN更新換代！性能提升算力減半，還即插即用(2019-4)

刷臉背後，卷積神經網絡的數學原理原來是這樣的(2019-4)

比CNN表現更好，CV領域全新卷積操作OctConv厲害在哪裡？(2019-4)

微軟亞洲研究院等提出CNN訓練新方法RePr，準確率顯著提升（2019-3）

基於深度CNN的腫瘤體細胞突變檢測工具（2019-3）

7大類深度CNN架構創新綜述

實踐類文章（5）

運用計算圖搭建卷積神經網絡（CNN）（2019-7）

怎樣設計最優的卷積神經網絡架構？| NAS原理剖析（2019-7）

40行Python代碼，實現卷積特徵可視化

使用Python和Mask R-CNN自動尋找停車位，這是什麼神操作？

CNN圖像分類策略簡單到出人意料！

受限玻爾茲曼機（Restricted Boltzmann machine | RBM）

百度百科版本

受限玻爾茲曼機（英語：restricted Boltzmann machine, RBM）是一種可通過輸入數據集學習概率分佈的隨機生成神經網絡。RBM最初由發明者保羅·斯模稜斯基於1986年命名為簧風琴（Harmonium），但直到傑弗里·辛頓及其合作者在2000年代中葉發明快速學習算法後，受限玻茲曼機才變得知名。受限玻茲曼機在降維、分類、協同過濾、特徵學習和主題建模中得到了應用。根據任務的不同，受限玻茲曼機可以使用監督學習或無監督學習的方法進行訓練。

查看詳情

 

維基百科版本

受限波爾茲曼機（RBM）是一種生成 隨機 的人工神經網絡，可以學習的概率分佈在其組輸入。

RBM最初是由Paul Smolensky於1986年以Harmonium的名稱發明的，並且在Geoffrey Hinton和合作者在2000年中期為他們發明快速學習算法之後突顯出來。RBM已經在降維，分類，協同過濾，特徵學習和主題建模中找到了應用。根據任務的不同， 他們可以通過監督或無人監督的方式接受培訓。

顧名思義，RBM是Boltzmann機器的變體，其限制是它們的神經元必須形成二分圖：來自兩組單元中的每一組的一對節點（通常稱為「可見」和「隱藏」）單元）可以在它們之間具有對稱連接; 並且組內的節點之間沒有連接。相比之下，「不受限制的」Boltzmann機器可能在隱藏單元之間有連接。這種限制允許比一般類別的玻爾茲曼機器更有效的訓練算法，特別是基於梯度的 對比發散算法。

受限制的玻爾茲曼機器也可用於深度學習網絡。特別地，深度置信網絡可以通過「堆疊」RBM並且可選地通過梯度下降和反向傳播來微調所得到的深度網絡來形成。

查看詳情

強化學習-Reinforcement learning | RL

一文看懂強化學習

強化學習是機器學習的一種學習方式，它跟監督學習、無監督學習是對應的。本文將詳細介紹強化學習的基本概念、應用場景和主流的強化學習算法及分類。

 

什麼是強化學習？

強化學習並不是某一種特定的算法，而是一類算法的統稱。

如果用來做對比的話，他跟監督學習，無監督學習 是類似的，是一種統稱的學習方式。

強化學習是機器學習的學習方法之一

強化學習算法的思路非常簡單，以遊戲為例，如果在遊戲中採取某種策略可以取得較高的得分，那麼就進一步「強化」這種策略，以期繼續取得較好的結果。這種策略與日常生活中的各種「績效獎勵」非常類似。我們平時也常常用這樣的策略來提高自己的遊戲水平。

在 Flappy bird 這個遊戲中，我們需要簡單的點擊操作來控制小鳥，躲過各種水管，飛的越遠越好，因為飛的越遠就能獲得更高的積分獎勵。

這就是一個典型的強化學習場景：

  • 機器有一個明確的小鳥角色——代理
  • 需要控制小鳥飛的更遠——目標
  • 整個遊戲過程中需要躲避各種水管——環境
  • 躲避水管的方法是讓小鳥用力飛一下——行動
  • 飛的越遠，就會獲得越多的積分——獎勵

遊戲是典型的強化學習場景

你會發現，強化學習和監督學習、無監督學習 最大的不同就是不需要大量的「數據餵養」。而是通過自己不停的嘗試來學會某些技能。

 

強化學習的應用場景

強化學習目前還不夠成熟，應用場景也比較局限。最大的應用場景就是遊戲了。

遊戲

強化學習在遊戲領域應用最多

2016年：AlphaGo Master 擊敗李世石，使用強化學習的 AlphaGo Zero 僅花了40天時間，就擊敗了自己的前輩 AlphaGo Master。

《被科學家譽為「世界壯舉」的AlphaGo Zero, 對普通人意味着什麼？》

2019年1月25日：AlphaStar 在《星際爭霸2》中以 10：1 擊敗了人類頂級職業玩家。

《星際爭霸2人類1:10輸給AI！DeepMind 「AlphaStar」進化神速》

2019年4月13日：OpenAI 在《Dota2》的比賽中戰勝了人類世界冠軍。

《2:0！Dota2世界冠軍OG，被OpenAI按在地上摩擦》

 

機械人

強化學習在機械人領域也有不少應用

機械人很像強化學習里的「代理」，在機械人領域，強化學習也可以發揮巨大的作用。

《機械人通過強化學習，可以實現像人一樣的平衡控制》

《深度學習與強化學習相結合，谷歌訓練機械臂的長期推理能力》

《伯克利強化學習新研究：機械人只用幾分鐘隨機數據就能學會軌跡跟蹤》

 

其他

強化學習在推薦系統，對話系統，教育培訓，廣告，金融等領域也有一些應用：

《強化學習與推薦系統的強強聯合》

《基於深度強化學習的對話管理中的策略自適應》

《強化學習在業界的實際應用》

 

強化學習的主流算法

免模型學習（Model-Free） vs 有模型學習（Model-Based）

在介紹詳細算法之前，我們先來了解一下強化學習算法的2大分類。這2個分類的重要差異是：智能體是否能完整了解或學習到所在環境的模型

有模型學習（Model-Based）對環境有提前的認知，可以提前考慮規劃，但是缺點是如果模型跟真實世界不一致，那麼在實際使用場景下會表現的不好。

免模型學習（Model-Free）放棄了模型學習，在效率上不如前者，但是這種方式更加容易實現，也容易在真實場景下調整到很好的狀態。所以免模型學習方法更受歡迎，得到更加廣泛的開發和測試。

 

主流的強化學習算法分類

免模型學習 – 策略優化（Policy Optimization）

這個系列的方法將策略顯示錶示為： \pi_{\theta}(a|s) 。 它們直接對性能目標 J(\pi_{\theta}) 進行梯度下降進行優化，或者間接地，對性能目標的局部近似函數進行優化。優化基本都是基於 同策略 的，也就是說每一步更新只會用最新的策略執行時採集到的數據。策略優化通常還包括學習出 V_{\phi}(s) ，作為 V^{\pi}(s) 的近似，該函數用於確定如何更新策略。

基於策略優化的方法舉例：

  • A2C / A3C, 通過梯度下降直接最大化性能
  • PPO , 不直接通過最大化性能更新，而是最大化 目標估計 函數，這個函數是目標函數 J(\pi_{\theta}) 的近似估計。

 

免模型學習 – Q-Learning

這個系列的算法學習最優行動值函數 Q^*(s,a) 的近似函數： Q_{\theta}(s,a) 。它們通常使用基於 貝爾曼方程 的目標函數。優化過程屬於 異策略 系列，這意味着每次更新可以使用任意時間點的訓練數據，不管獲取數據時智能體選擇如何探索環境。對應的策略是通過 Q^*and \pi^* 之間的聯繫得到的。智能體的行動由下面的式子給出：

a(s) = \arg \max_a Q_{\theta}(s,a).

基於 Q-Learning 的方法

  • DQN, 一個讓深度強化學習得到發展的經典方法
  • 以及 C51, 學習關於回報的分佈函數，其期望是 Q^*

 

有模型學習 – 純規劃

這種最基礎的方法，從來不顯示的表示策略，而是純使用規劃技術來選擇行動，例如 模型預測控制 (model-predictive control, MPC)。在模型預測控制中，智能體每次觀察環境的時候，都會計算得到一個對於當前模型最優的規劃，這裡的規劃指的是未來一個固定時間段內，智能體會採取的所有行動（通過學習值函數，規划算法可能會考慮到超出範圍的未來獎勵）。智能體先執行規劃的第一個行動，然後立即捨棄規劃的剩餘部分。每次準備和環境進行互動時，它會計算出一個新的規劃，從而避免執行小於規劃範圍的規劃給出的行動。

  • MBMF 在一些深度強化學習的標準基準任務上，基於學習到的環境模型進行模型預測控制

 

有模型學習 – Expert Iteration

純規劃的後來之作，使用、學習策略的顯示錶示形式： \pi_{\theta}(a|s) 。智能體在模型中應用了一種規划算法，類似蒙特卡洛樹搜索(Monte Carlo Tree Search)，通過對當前策略進行採樣生成規劃的候選行為。這種算法得到的行動比策略本身生成的要好，所以相對於策略來說，它是「專家」。隨後更新策略，以產生更類似於規划算法輸出的行動。

  • ExIt 算法用這種算法訓練深層神經網絡來玩 Hex
  • AlphaZero 這種方法的另一個例子

 

除了免模型學習和有模型學習的分類外，強化學習還有其他幾種分類方式：

  • 基於概率 VS 基於價值
  • 回合更新 VS 單步更新
  • 在線學習 VS 離線學習

詳細請查看《強化學習方法匯總 》

 

百度百科和維基百科

百度百科版本

強化學習(reinforcement learning)，又稱再勵學習、評價學習，是一種重要的機器學習方法，在智能控制機械人及分析預測等領域有許多應用。

但在傳統的機器學習分類中沒有提到過強化學習，而在連接主義學習中，把學習算法分為三種類型，即非監督學習(unsupervised learning)、監督學習(supervised leaning)和強化學習。

查看詳情

維基百科版本

強化學習（RL）是機器學習的一個領域，涉及軟件代理如何在環境中採取行動以最大化一些累積獎勵的概念。該問題由於其一般性，在許多其他學科中得到研究，如博弈論，控制理論，運籌學，信息論，基於仿真的優化，多智能體系統，群智能，統計和遺傳算法。。在運籌學和控制文獻中，強化學習被稱為近似動態規劃或神經動態規劃。

查看詳情

 

入門類文章（5）

【強化學習】從強化學習基礎概念開始（2019-6）

強化學習如何入門？看這篇文章就夠了

強化學習通俗導論（一）：什麼是強化學習

「教程」深度學習、強化學習進階課程（YouTube視頻，需要科學上網）

強化學習掃盲

實踐類文章（4）

使用Python進行強化學習的編程方法(2019-4-3)

乾貨 | 強化學習中，如何從稀疏和不明確的反饋中學習泛化(2019-3-1)

一文了解強化學習的商業應用

深度解讀AlphaGo Zero，教你訓練一個「圍棋高手」

開拓視野類文章（4）

強化學習在現實世界中的應用（2019-4-3）

谷歌新方法加速深度強化學習的訓練過程（2019-3-27）

強化學習遭遇瓶頸！分層RL將成為突破的希望（2019-3-23）

好奇心驅動的強化學習（2018-10）（需要科學上網）

讓智能體主動交互，DeepMind提出用元強化學習實現因果推理

相關資源（1）

DeepMind開源強化學習庫TRFL

自編碼器（Autoencoder）

百度百科版本

自編碼，又稱自編碼器（autoencoder），是神經網絡的一種，經過訓練後能嘗試將輸入複製到輸出。自編碼器（autoencoder）內部有一個隱藏層h，可以產生編碼（code）表示輸入。該網絡可以看作由兩部分組成：一個由函數h = f(x) 表示的編碼器和一個生成重構的解碼器r = g(h)。

查看詳情

 

維基百科版本

自動編碼器是一種類型的人工神經網絡用於學習高效的數據值編碼以無監督方式。自動編碼器的目的是學習一組數據的表示（編碼），通常用於降低維數。與縮小側一起，學習重建側，其中自動編碼器嘗試從縮減編碼生成儘可能接近其原始輸入的表示，因此其名稱。

查看詳情

前饋神經網絡（Feedforward neural network）

百度百科版本

前饋神經網絡是一種最簡單的神經網絡，各神經元分層排列。每個神經元只與前一層的神經元相連。接收前一層的輸出，並輸出給下一層．各層間沒有反饋。是目前應用最廣泛、發展最迅速的人工神經網絡之一。研究從20世紀60年代開始，目前理論研究和實際應用達到了很高的水平。

查看詳情

 

維基百科版本

前饋神經網絡是一種人工神經網絡，其中，所述節點之間的連接就不能形成循環。[1]因此，它與遞歸神經網絡不同。

前饋神經網絡是第一種也是最簡單的人工神經網絡設計。在該網絡中，信息僅在一個方向上移動，從輸入節點向前移動，通過隱藏節點（如果有的話）移動到輸出節點。網絡中沒有循環或循環。

查看詳情

模糊神經網絡（Neuro-fuzzy | FNN）

百度百科版本

模糊神經網絡就是模糊理論同神經網絡相結合的產物，它彙集了神經網絡與模糊理論的優點，集學習、聯想、識別、信息處理於一體。

查看詳情

 

維基百科版本

神經模糊雜交導致混合智能系統通過將模糊系統的類人推理風格與神經網絡的學習和連接結構相結合來協同這兩種技術。神經模糊雜交在文獻中被廣泛稱為模糊神經網絡（FNN）或神經模糊系統（NFS）。神經模糊系統（此後更常用的術語）通過使用模糊集和由一組IF-THEN模糊規則組成的語言模型，結合了類似人類的模糊系統推理方式。神經模糊系統的主要優勢在於它們是通用逼近器，能夠徵求可解釋的IF-THEN規則。

查看詳情

自組織映射（Self-organization map | SOM）

百度百科版本

自組織神經網絡SOM是基於無監督學習方法的神經網絡的一種重要類型。自組織映射網絡理論最早是由芬蘭赫爾辛基理工大學Kohen於1981年提出的。此後，伴隨着神經網絡在20世紀80年代中後期的迅速發展，自組織映射理論及其應用也有了長足的進步。

查看詳情

 

維基百科版本

自組織映射（SOM）或自組織特徵映射（SOFM）是一種類型的人工神經網絡（ANN），其使用已訓練的無監督學習以產生低維（通常為二維），離散的表示訓練樣本的輸入空間，稱為地圖，因此是一種減少維數的方法。自組織映射與其他人工神經網絡不同，因為它們應用競爭學習而不是糾錯學習（例如具有梯度下降的反向傳播）），從某種意義上說，他們使用鄰域函數來保留輸入空間的拓撲屬性。

這使得SOM 通過創建高維數據的低維視圖（類似於多維縮放）對可視化非常有用。芬蘭教授Teuvo Kohonen在20世紀80年代引入的人工神經網絡有時被稱為Kohonen地圖或網絡。Kohonen網是一種計算上方便的抽象，建立在20世紀70年代神經系統的生物模型上和形態發生模型可追溯到20世紀50年代的阿蘭圖靈。

查看詳情

K均值聚類（k-means clustering）

K均值聚類的優缺點

優點

  • 算法簡單，容易實現 ；
  • 算法速度很快；
  • 對處理大數據集，該算法是相對可伸縮的和高效率的，因為它的複雜度大約是O(nkt)，其中n是所有對象的數目，k是簇的數目,t是迭代的次數。通常k<<n。這個算法通常局部收斂。
  • 算法嘗試找出使平方誤差函數值最小的k個劃分。當簇是密集的、球狀或團狀的，且簇與簇之間區別明顯時，聚類效果較好。

缺點

  • 對數據類型要求較高，適合數值型數據；
  • 可能收斂到局部最小值，在大規模數據上收斂較慢
  • 分組的數目k是一個輸入參數，不合適的k可能返回較差的結果。
  • 對初值的簇心值敏感，對於不同的初始值，可能會導致不同的聚類結果；
  • 不適合於發現非凸面形狀的簇，或者大小差別很大的簇。
  • 對於」噪聲」和孤立點數據敏感，少量的該類數據能夠對平均值產生極大影響。

 

百度百科版本

K均值聚類算法是先隨機選取K個對象作為初始的聚類中心。然後計算每個對象與各個種子聚類中心之間的距離，把每個對象分配給距離它最近的聚類中心。聚類中心以及分配給它們的對象就代表一個聚類。一旦全部對象都被分配了，每個聚類的聚類中心會根據聚類中現有的對象被重新計算。這個過程將不斷重複直到滿足某個終止條件。終止條件可以是沒有（或最小數目）對象被重新分配給不同的聚類，沒有（或最小數目）聚類中心再發生變化，誤差平方和局部最小。

查看詳情

 

維基百科版本

ķ -means聚類是的方法的矢量量化，最初來自信號處理，即流行聚類分析在數據挖掘。ķ -means聚類的目的是劃分 Ñ觀測到 ķ其中每個觀測屬於簇群集與最近的平均值，作為原型群集的。這導致數據空間劃分為 Voronoi單元。

問題在計算上很困難（NP難）; 然而，有效的啟發式算法快速收斂到局部最優。這些通常是類似於最大期望算法為混合物的高斯分佈經由通過兩個採用的迭代細化方法k-均值和高斯混合模型。他們都使用集群中心來建模數據; 然而，k -means聚類傾向於找到具有可比空間範圍的聚類，而期望最大化機制允許聚類具有不同的形狀。

該算法與k最近鄰分類器有鬆散的關係，這是一種流行的分類機器學習技術，由於名稱的原因，它經常與k -means 混淆。應用1最近鄰分類器，通過k -means 獲得的聚類中心將新數據分類到現有聚類中。這被稱為最近的質心分類器或Rocchio算法。

查看詳情

反向傳播算法（Backpropagation）

百度百科版本

BP算法(即反向傳播算法)是在有導師指導下，適合於多層神經元網絡的一種學習算法，它建立在梯度下降法的基礎上。BP網絡的輸入輸出關係實質上是一種映射關係：一個n輸入m輸出的BP神經網絡所完成的功能是從n維歐氏空間向m維歐氏空間中一有限域的連續映射，這一映射具有高度非線性。它的信息處理能力來源於簡單非線性函數的多次複合，因此具有很強的函數復現能力。這是BP算法得以應用的基礎。

查看詳情

 

維基百科版本

反向傳播是一種用於人工神經網絡的方法，用於計算在網絡中使用的權重的計算中所需的梯度。反向傳播是「錯誤的向後傳播」的簡寫，因為錯誤在輸出端計算並在整個網絡層中向後分佈。它通常用於訓練深度神經網絡。

反向傳播是將delta規則推廣到多層前饋網絡，通過使用鏈規則迭代計算每個層的梯度來實現。它與Gauss-Newton算法密切相關，是神經反向傳播研究的一部分。

反向傳播是一種稱為自動微分的更通用技術的特例。在學習的情況下，反向傳播通常使用的梯度下降優化算法通過計算來調節神經元的權重梯度的的損失函數。

查看詳情