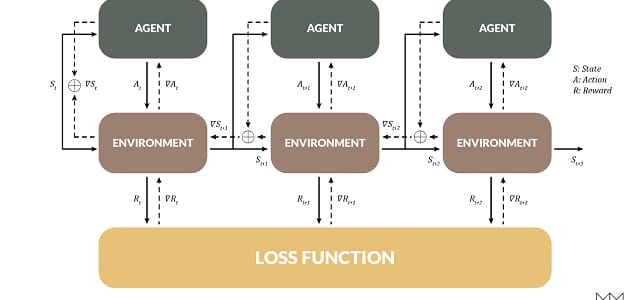
我们讨论了可区分编程的概念,我们将现有程序整合到深度学习模型中。但是,如果你是一名研究人员,比如一辆自动驾驶汽车,那么可区分编程在实践中意味着什么呢?它如何影响我们表达问题的方式,训练我们的模型,策划我们的数据集,以及最终我们实现的结果?
本文展示了DP可以为一些简单但经典的控制问题带来什么,我们通常会使用强化学习(RL)。基于DP的模型不仅学习了比RL更有效的控制策略,而且还能更快地训练数量级。该代码是所有可用来为自己运行的-他们会在几秒钟内大部分列车上的任何笔记本电脑。
跟随渐变
差异化是深度学习的关键; 给定函数y = f(x)y = f(x)我们使用gradient \ frac {dy} {dx} dxdy来计算xx的变化将如何影响yy。尽管有数学服装,但渐变实际上是一个非常通用和直观的概念。忘掉你在学校必须盯着的公式; 让我们做一些更有趣的事情,比如扔东西。

当我们用投石机扔东西时,我们的xx代表一个设置(比如,配重的大小,或释放角度),而yy是射弹在着陆前行进的距离。如果你想瞄准,渐变会告诉你一些非常有用的东西 – 目标的改变是增加还是减少距离。要最大化距离,只需按照渐变。
好吧,但我们怎么能得到这个神奇的数字呢?诀窍是一个称为算法区分的过程,它不仅可以区分你在学校学到的简单公式,还可以区分任何复杂程序 – 比如我们的投石机模拟器。结果是我们可以采用一个简单的模拟器,用Julia和DiffEq编写,没有深入学习,并在单个函数调用中获得渐变。
# what you did in school
gradient(x -> 3x^2 + 2x + 1, 5) # (32,)
# something a little more advanced
gradient((wind, angle, weight) -> Trebuchet.shoot(wind, angle, weight),
-2, 45, 200) # (4.02, -0.99, 0.051)现在我们有了它,让我们用它做一些有趣的事情。
扔东西
使用它的一种简单方法是将投石机对准目标,使用渐变来微调释放角度; 这种事情在参数估计的名义下很常见,我们之前已经介绍了类似的例子。我们可以通过meta来使事情变得更有趣:不是在给定单个目标的情况下瞄准投石机,我们将优化可以针对任何目标瞄准它的神经网络。以下是它的工作原理:神经网络有两个输入,目标距离(米)和当前风速。网络吐出投入设置的投石机设置(配重的质量和释放角度),模拟器计算实现的距离。然后我们与目标进行比较,并在整个链中反向传播,端到端,调整网络的权重。我们的“数据集”是一组随机选择的目标和风速。
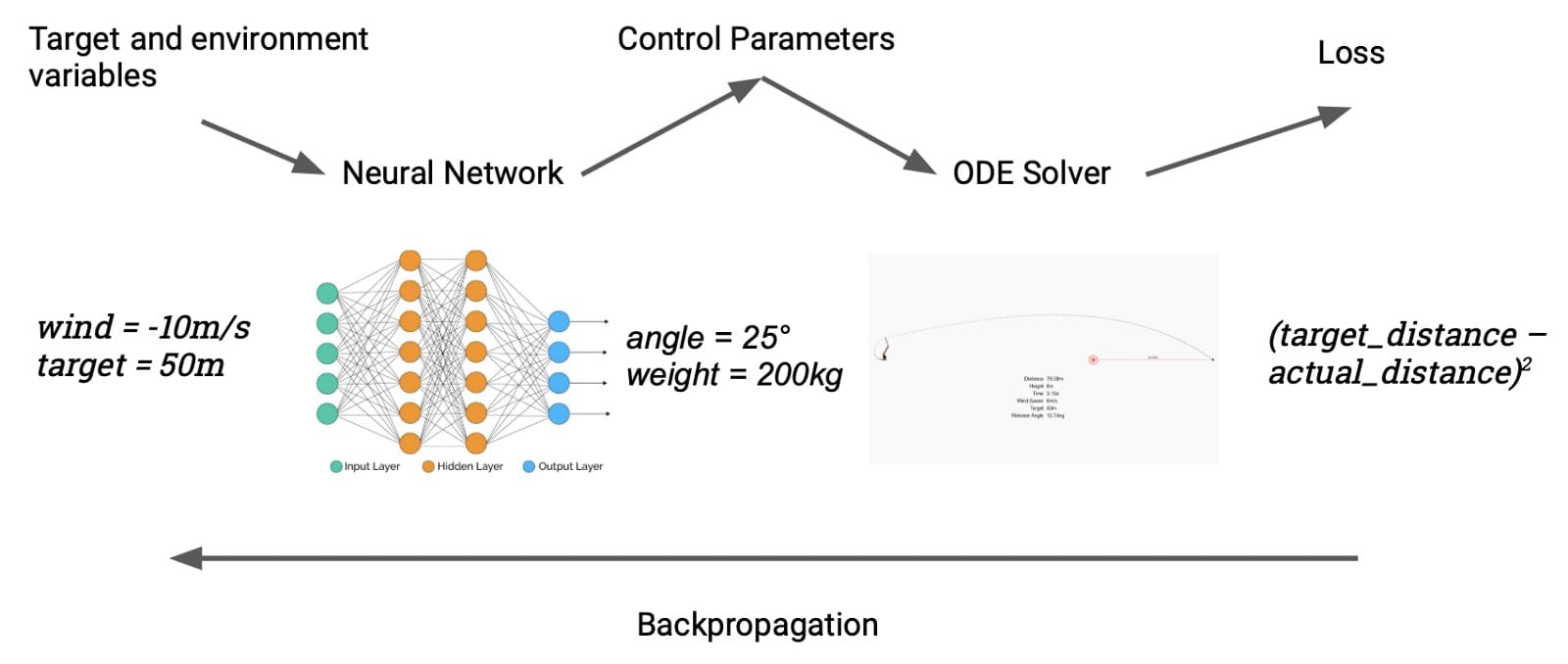
这个简单模型的一个很好的特性就是训练它很快,因为我们已经完全以可微分的方式表达了我们对模型的要求。最初,它看起来像这样:

经过大约五分钟的培训(在我的笔记本电脑CPU的单核上),它看起来像这样:

如果你想尝试推动它,请调高风速:

它只有16厘米,或约0.3%。
这是关于最简单的控制问题,我们主要用于说明目的。但是,我们可以以更高级的方式将相同的技术应用于经典的RL问题。
购物车,遇见波兰人
一个更容易识别的控制问题是CartPole,这是强化学习的“你好世界”。任务是通过向左或向右推动其基座来学习平衡直立杆。我们的设置大致类似于投石机案:Julia实施意味着我们可以直接将环境产生的奖励视为损失。DP允许我们从无模型转换为基于模型的RL无缝切换。
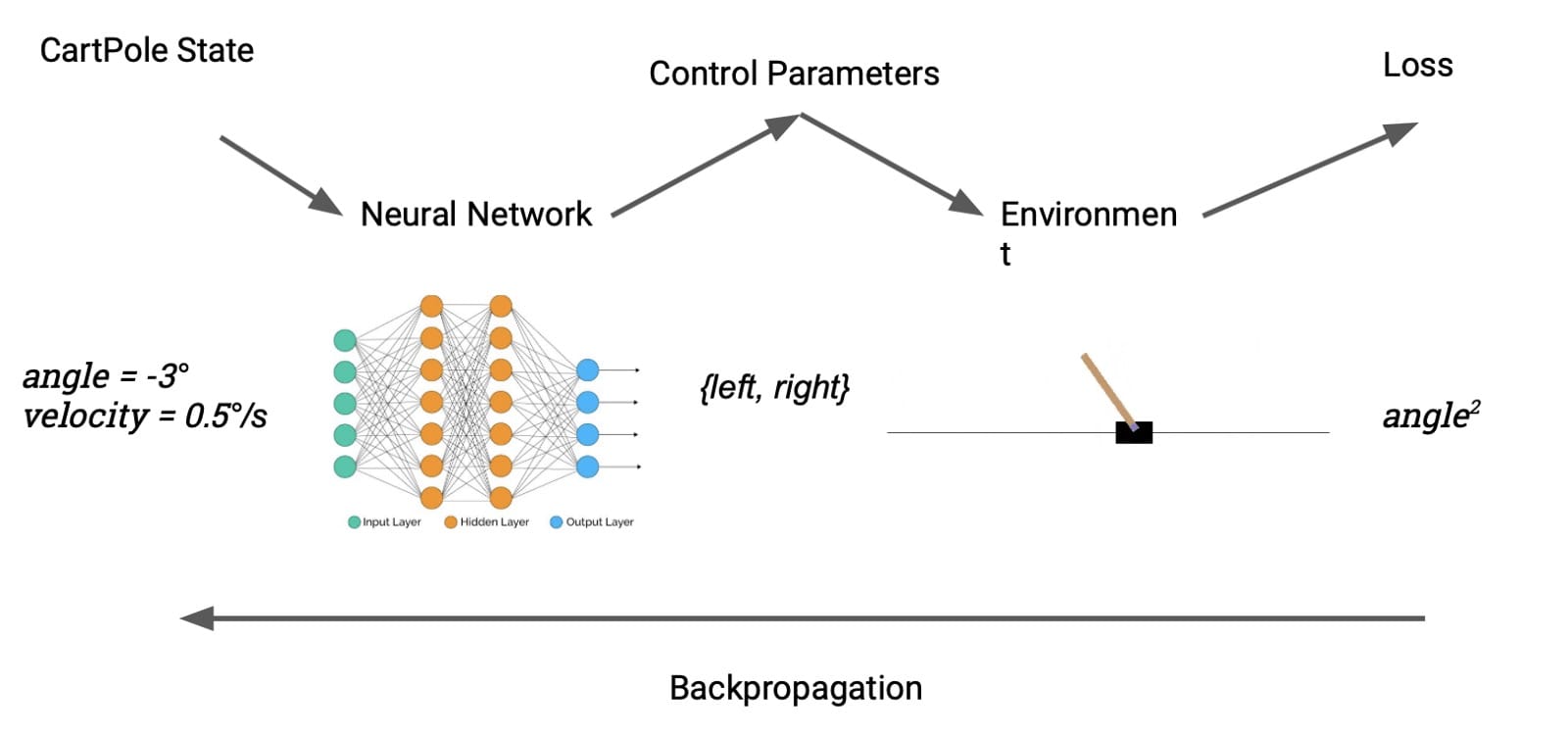
精明的读者可能会注意到一个障碍。cartpole的动作空间 – 向左或向右轻推 – 是离散的,因此不可区分。我们通过引入可区分的离散化来解决这个问题,定义如下:
\ begin {aligned} f(x)&amp; = \ begin {cases} 1&amp; x \ ge 0 \\ -1&amp; x&lt; 0 \ end {cases} \\ \ frac {df} {dx}&amp; = 1 \ end {aligned} f(x)dxdf = {1-1x≥0x<0 = 1
换句话说,我们强制渐变表现得好像ff是身份函数。鉴于可分性的数学概念已经在ML中滥用了多少,我们可以在这里作弊也许并不奇怪; 对于训练我们需要的是一个信号来通知参数空间的伪随机游走,其余的是细节。
结果不言自明。在解决问题之前,RL方法需要训练数百集,DP模型只需要大约5集才能最终获胜。

通过时间的钟摆和Backprop
RL的一个重要目标是处理延迟奖励,当一个行动在将来的几个步骤之前帮助我们时。DP也允许这样做,并且以一种非常熟悉的方式:当环境可以区分时,我们实际上可以使用反向传播来训练代理,就像一个经常性的网络!在这种情况下,环境状态变为在时间步长之间变化的“隐藏状态”。
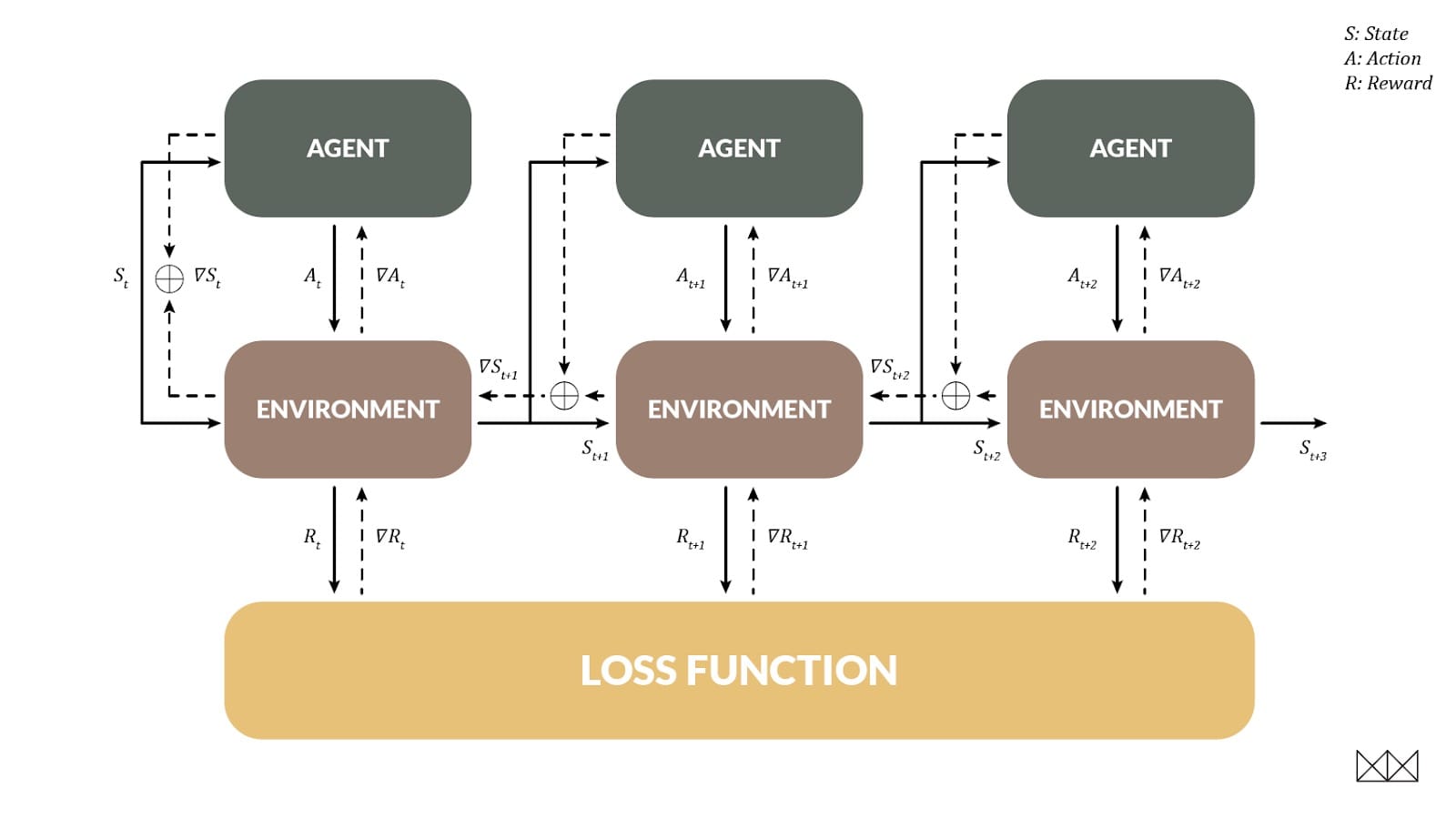
为了展示这种技术,我们研究了摆锤环境,其任务是摆锤直到它直立,以最小的努力保持平衡。这对RL型号来说很难; 在大约20次训练之后,问题得以解决,但通常解决方案的路径明显不是最佳的。相比之下,BPTT可以在一集训练中击败RL排行榜。实际观看这一集展开是有益的; 在记录开始时,策略是随机的,并且模型随着时间的推移而改进。学习的速度几乎令人担忧。

尽管只是经历了一集,但该模型很好地处理了任何初始角度,并且具有非常接近最优策略的东西。重新启动时,模型看起来更像这样。

这仅仅是个开始; 我们将获得真正的胜利,将DP应用于对RL来说太难以使用的环境。
地图不是领土
这些玩具模型的局限在于它们将模拟的训练环境与测试环境等同起来; 当然,现实世界并不是可以区分的。在一个更现实的模型中,模拟为我们提供了一个粗略的行为概述,并用数据进行了细化。该数据通知(比如说)风的模拟效果,进而改善模拟器传递给控制器的梯度质量。模型甚至可以构成控制器前向传递的一部分,使其能够优化其预测,而无需从头开始学习系统动态。探索这些新架构将有助于激发未来的工作。
结尾
核心思想是可区分编程,我们只需编写任意数字程序并通过渐变进行优化,这是一种提供更好的深度学习模型和体系结构的强大方法 – 特别是当我们拥有一个可识别的大型代码库时手。所描述的玩具模型实际上只是预览,但我们希望他们能够直观地了解如何以更现实的方式应用这些想法。
正如函数式编程涉及使用函数模式推理和表达算法一样,可微分编程涉及使用可微分模式表达算法。许多这样的设计模式已经由深度学习社区开发,例如用于处理控制问题或序列和ttree结构化数据。这篇文章介绍了几个新的,随着领域的成熟,将会发明更多。由此产生的程序可能会使最先进的当前深度学习架构看起来相形见绌。
本文转自medium,原文地址



Comments