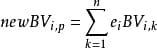網絡轉載版本
要描述 LDA 模型,就要說一下 LDA 模型所屬的產生式模型的背景。產生式模型是相對於判別式模型而說的。這裡,我們假設需要建模的數據有特徵信息,也就是通常說的 X,以及標籤信息,也就是通常所說的 Y。
判別式模型常常直接對 Y 的產生過程(Generative Process) 進行描述,而對特徵信息本身不予建模。這使得判別式模型天生就成為構建分類器或者回歸分析的有利工具。而產生式模型則要同時對 X 和 Y 建模,這使得產生式模型更適合做無標籤的數據分析,比如聚類。當然,因為產生式模型要對比較多的信息進行建模,所以一般認為對於同一個數據而言,產生式模型要比判別式模型更難以學習。
一般來說,產生式模型希望通過一個產生過程來幫助讀者理解一個模型。注意,這個產生過程本質是描述一個聯合概率分佈(Joint Distribution)的分解過程。也就是說,這個過程是一個虛擬過程,真實的數據往往並不是這樣產生的。這樣的產生過程是模型的一個假設,一種描述。任何一個產生過程都可以在數學上完全等價一個聯合概率分佈。
LDA 的產生過程描述了文檔以及文檔中文字的生成過程。在原始的 LDA 論文中,作者們描述了對於每一個文檔而言有這麼一種生成過程:
- 首先,從一個全局的泊松(Poisson)參數為β的分佈中生成一個文檔的長度 N;
- 從一個全局的狄利克雷(Dirichlet)參數為α的分佈中生成一個當前文檔的θ;
- 然後對於當前文檔長度 N 的每一個字執行以下兩步,一是從以θ為參數的多項(Multinomial)分佈中生成一個主題(Topic)的下標(Index)z_n;二是從以φ和 z 共同為參數的多項分佈中產生一個字(Word)w_n。
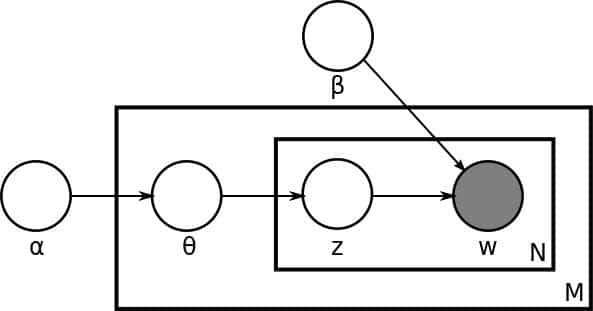
從這個描述我們可以馬上得到這些重要的模型信息。第一,我們有一個維度是 K 乘以 V 的主題矩陣(Topic Matrix)。其中每一行都是一個φ,也就是某一個生成字的多項分佈。當然,這個主題矩陣我們在事先並不知道,是需要學習得到的。另外,對每一個文檔而言,θ是一個長度為 K 的向量,用於描述當前文檔在 K 個主題上的分佈。產生過程告訴我們,我們對於文檔中的每一個字,都先從這個θ向量中產生一個下標,用於告訴我們現在要從主題矩陣中的哪一行去生成當前的字。
上面內容轉自《AI技術內參》,是一個很不錯的付費教程,推薦大家訂閱。

百度百科版本
LDA(Latent Dirichlet Allocation)是一種文檔主題生成模型,也稱為一個三層貝葉斯概率模型,包含詞、主題和文檔三層結構。所謂生成模型,就是說,我們認為一篇文章的每個詞都是通過「以一定概率選擇了某個主題,並從這個主題中以一定概率選擇某個詞語」這樣一個過程得到。文檔到主題服從多項式分佈,主題到詞服從多項式分佈。
LDA是一種非監督機器學習技術,可以用來識別大規模文檔集(document collection)或語料庫(corpus)中潛藏的主題信息。它採用了詞袋(bag of words)的方法,這種方法將每一篇文檔視為一個詞頻向量,從而將文本信息轉化為了易於建模的數字信息。但是詞袋方法沒有考慮詞與詞之間的順序,這簡化了問題的複雜性,同時也為模型的改進提供了契機。每一篇文檔代表了一些主題所構成的一個概率分佈,而每一個主題又代表了很多單詞所構成的一個概率分佈。
維基百科版本
在自然語言處理中,潛在Dirichlet分配(LDA)是一種生成統計模型,它允許未觀察到的組解釋觀察集,解釋為什麼數據的某些部分是相似的。例如,如果觀察是收集到文檔中的單詞,則假定每個文檔是少量主題的混合,並且每個單詞的存在可歸因於文檔的主題之一。LDA是主題模型的示例。